Learning Outcomes
- Verify the fundamental trigonometric identities.
- Simplify trigonometric expressions using algebra and the identities.
- Use sum and difference formulas for cosine.
- Use sum and difference formulas for sine.
- Use sum and difference formulas for tangent.
- Use sum and difference formulas for cofunctions.
- Use sum and difference formulas to verify identities.
- Use double-angle formulas to find exact values.
- Use double-angle formulas to verify identities.
- Use reduction formulas to simplify an expression.
- Use half-angle formulas to find exact values.
Verify the fundamental trigonometric identities
Identities enable us to simplify complicated expressions. They are the basic tools of trigonometry used in solving trigonometric equations, just as factoring, finding common denominators, and using special formulas are the basic tools of solving algebraic equations. In fact, we use algebraic techniques constantly to simplify trigonometric expressions. Basic properties and formulas of algebra, such as the difference of squares formula and the perfect squares formula, will simplify the work involved with trigonometric expressions and equations. We already know that all of the trigonometric functions are related because they all are defined in terms of the unit circle. Consequently, any trigonometric identity can be written in many ways.
To verify the trigonometric identities, we usually start with the more complicated side of the equation and essentially rewrite the expression until it has been transformed into the same expression as the other side of the equation. Sometimes we have to factor expressions, expand expressions, find common denominators, or use other algebraic strategies to obtain the desired result. In this first section, we will work with the fundamental identities: the Pythagorean identities, the even-odd identities, the reciprocal identities, and the quotient identities.
We will begin with the Pythagorean identities, which are equations involving trigonometric functions based on the properties of a right triangle. We have already seen and used the first of these identifies, but now we will also use additional identities.
| Pythagorean Identities | ||
|---|---|---|
| [latex]{\sin }^{2}\theta +{\cos }^{2}\theta =1[/latex] | [latex]1+{\cot }^{2}\theta ={\csc }^{2}\theta[/latex] | [latex]1+{\tan }^{2}\theta ={\sec }^{2}\theta[/latex] |
The second and third identities can be obtained by manipulating the first. The identity [latex]1+{\cot }^{2}\theta ={\csc }^{2}\theta\[/latex] is found by rewriting the left side of the equation in terms of sine and cosine.
Prove: [latex]1+{\cot }^{2}\theta ={\csc }^{2}\theta /latex]
Similarly, [latex]1+{\tan }^{2}\theta ={\sec }^{2}\theta[/latex] can be obtained by rewriting the left side of this identity in terms of sine and cosine. This gives
The next set of fundamental identities is the set of even-odd identities. The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle and determine whether the identity is odd or even.
| Even-Odd Identities | ||
|---|---|---|
| [latex]\begin{gathered}\tan \left(-\theta \right)=-\tan \theta\\ \cot \left(-\theta \right)=-\cot \theta \end{gathered}[/latex] | [latex]\begin{gathered}\sin \left(-\theta \right)=-\sin \theta\\ \csc \left(-\theta \right)=-\csc \theta\end{gathered}[/latex] | [latex]\begin{gathered}\cos \left(-\theta \right)=\cos \theta \\ \sec \left(-\theta \right)=\sec \theta \end{gathered}[/latex] |
Recall that an odd function is one in which [latex]f\left(-x\right)= -f\left(x\right)[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex]. The sine function is an odd function because [latex]\sin \left(-\theta \right)=-\sin \theta[/latex]. The graph of an odd function is symmetric about the origin. For example, consider corresponding inputs of [latex]\frac{\pi }{2}\\[/latex] and [latex]-\frac{\pi }{2}[/latex]. The output of [latex]\sin \left(\frac{\pi }{2}\right)[/latex] is opposite the output of [latex]\sin \left(-\frac{\pi }{2}\right)[/latex]. Thus,
This is shown in Figure 2.

Figure 2. Graph of [latex]y=\sin \theta[/latex]
Recall that an even function is one in which
The graph of an even function is symmetric about the y-axis. The cosine function is an even function because [latex]\cos \left(-\theta \right)=\cos \theta[/latex].
For example, consider corresponding inputs [latex]\frac{\pi }{4}[/latex] and [latex]-\frac{\pi }{4}[/latex]. The output of [latex]\cos \left(\frac{\pi }{4}\right)[/latex] is the same as the output of [latex]\cos \left(-\frac{\pi }{4}\right)[/latex]. Thus,
See Figure 3.
Figure 3. Graph of [latex]y=\cos \theta[/latex]
For all [latex]\theta[/latex] in the domain of the sine and cosine functions, respectively, we can state the following:
- Since [latex]\sin \left(-\theta \right)=-\sin \theta[/latex], sine is an odd function.
- Since, [latex]\cos \left(-\theta \right)=\cos \theta[/latex], cosine is an even function.
The other even-odd identities follow from the even and odd nature of the sine and cosine functions. For example, consider the tangent identity, [latex]\tan \left(-\theta \right)=\mathrm{-tan}\theta[/latex]. We can interpret the tangent of a negative angle as [latex]\tan \left(-\theta \right)=\frac{\sin \left(-\theta \right)}{\cos \left(-\theta \right)}=\frac{-\sin \theta }{\cos \theta }=-\tan \theta[/latex]. Tangent is therefore an odd function, which means that [latex]\tan \left(-\theta \right)=-\tan \left(\theta \right)[/latex] for all [latex]\theta[/latex] in the domain of the tangent function.
The cotangent identity, [latex]\cot \left(-\theta \right)=-\cot \theta[/latex], also follows from the sine and cosine identities. We can interpret the cotangent of a negative angle as [latex]\cot \left(-\theta \right)=\frac{\cos \left(-\theta \right)}{\sin \left(-\theta \right)}=\frac{\cos \theta }{-\sin \theta }=-\cot \theta[/latex]. Cotangent is therefore an odd function, which means that [latex]\cot \left(-\theta \right)=-\cot \left(\theta \right)[/latex] for all [latex]\theta[/latex] in the domain of the cotangent function.
The cosecant function is the reciprocal of the sine function, which means that the cosecant of a negative angle will be interpreted as [latex]\csc \left(-\theta \right)=\frac{1}{\sin \left(-\theta \right)}=\frac{1}{-\sin \theta }=-\csc \theta[/latex]. The cosecant function is therefore odd.
Finally, the secant function is the reciprocal of the cosine function, and the secant of a negative angle is interpreted as [latex]\sec \left(-\theta \right)=\frac{1}{\cos \left(-\theta \right)}=\frac{1}{\cos \theta }=\sec \theta[/latex]. The secant function is therefore even.
To sum up, only two of the trigonometric functions, cosine and secant, are even. The other four functions are odd, verifying the even-odd identities.
The next set of fundamental identities is the set of reciprocal identities, which, as their name implies, relate trigonometric functions that are reciprocals of each other.
| Reciprocal Identities | |
|---|---|
| [latex]\sin \theta =\frac{1}{\csc \theta }[/latex] | [latex]\csc \theta =\frac{1}{\sin \theta }[/latex] |
| [latex]\cos \theta =\frac{1}{\sec \theta }[/latex] | [latex]\sec \theta =\frac{1}{\cos \theta }[/latex] |
| [latex]\tan \theta =\frac{1}{\cot \theta }[/latex] | [latex]\cot \theta =\frac{1}{\tan \theta }[/latex] |
The final set of identities is the set of quotient identities, which define relationships among certain trigonometric functions and can be very helpful in verifying other identities.
| Quotient Identities | |
|---|---|
| [latex]\tan \theta =\frac{\sin \theta }{\cos \theta }[/latex] | [latex]\cot \theta =\frac{\cos \theta }{\sin \theta }[/latex] |
The reciprocal and quotient identities are derived from the definitions of the basic trigonometric functions.
A General Note: Summarizing Trigonometric Identities
The Pythagorean identities are based on the properties of a right triangle.
[latex]\begin{gathered} {\cos}^{2}\theta + {\sin}^{2}\theta=1 \\ 1+{\tan}^{2}\theta={\sec}^{2}\theta \\ 1+{\cot}^{2}\theta={\csc}^{2}\theta\end{gathered}[/latex]
The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle.
[latex]\begin{gathered} \cos(-\theta)=\cos(\theta) \\\sin(-\theta)=-\sin(\theta) \\\tan(-\theta)=-\tan(\theta) \\\cot(-\theta)=-\cot(\theta) \\\sec(-\theta)=\sec(\theta) \\\csc(-\theta)=-\csc(\theta) \end{gathered}[/latex]
The reciprocal identities define reciprocals of the trigonometric functions.
[latex]\begin{gathered}\sin\theta=\frac{1}{\csc\theta} \\ \cos\theta=\frac{1}{\sec\theta} \\ \tan\theta=\frac{1}{\cot\theta} \\ \cot\theta=\frac{1}{\tan\theta} \\ \sec\theta=\frac{1}{\cos\theta} \\ \csc\theta=\frac{1}{\sin\theta}\end{gathered}[/latex]
The quotient identities define the relationship among the trigonometric functions.
[latex]\begin{gathered} \tan\theta=\frac{\sin\theta}{\cos\theta} \\ \cot\theta=\frac{\cos\theta}{\sin\theta} \end{gathered}[/latex]
Example 1: Graphing the Equations of an Identity
Graph both sides of the identity [latex]\cot \theta =\frac{1}{\tan \theta }[/latex]. In other words, on the graphing calculator, graph [latex]y=\cot \theta[/latex] and [latex]y=\frac{1}{\tan \theta }[/latex].
How To: Given a trigonometric identity, verify that it is true.
- Work on one side of the equation. It is usually better to start with the more complex side, as it is easier to simplify than to build.
- Look for opportunities to factor expressions, square a binomial, or add fractions.
- Noting which functions are in the final expression, look for opportunities to use the identities and make the proper substitutions.
- If these steps do not yield the desired result, try converting all terms to sines and cosines.
Example 2: Verifying a Trigonometric Identity
Verify [latex]\tan \theta \cos \theta =\sin \theta[/latex].
Try It
Verify the identity [latex]\csc \theta \cos \theta \tan \theta =1[/latex].
Example 3: Verifying the Equivalency Using the Even-Odd Identities
Verify the following equivalency using the even-odd identities:
[latex]\left(1+\sin x\right)\left[1+\sin \left(-x\right)\right]={\cos }^{2}x[/latex]
Example 4: Verifying a Trigonometric Identity Involving sec2θ
Verify the identity [latex]\frac{{\sec }^{2}\theta -1}{{\sec }^{2}\theta }={\sin }^{2}\theta[/latex]
Analysis
In the first method, we used the identity [latex]{\sec }^{2}\theta ={\tan }^{2}\theta +1\\[/latex] and continued to simplify. In the second method, we split the fraction, putting both terms in the numerator over the common denominator. This problem illustrates that there are multiple ways we can verify an identity. Employing some creativity can sometimes simplify a procedure. As long as the substitutions are correct, the answer will be the same.
Try It
Show that [latex]\frac{\cot \theta }{\csc \theta }=\cos \theta[/latex].
Example 5: Creating and Verifying an Identity
Create an identity for the expression [latex]2\tan \theta \sec \theta[/latex] by rewriting strictly in terms of sine.
Example 6: Verifying an Identity Using Algebra and Even/Odd Identities
Verify the identity:
[latex]\begin{align}\frac{{\sin }^{2}\left(-\theta \right)-{\cos }^{2}\left(-\theta \right)}{\sin \left(-\theta \right)-\cos \left(-\theta \right)}=\cos \theta -\sin \theta\end{align}[/latex]
Try It
Verify the identity [latex]\frac{{\sin }^{2}\theta -1}{\tan \theta \sin \theta -\tan \theta }=\frac{\sin \theta +1}{\tan \theta }[/latex].
Example 7: Verifying an Identity Involving Cosines and Cotangents
Verify the identity: [latex]\left(1-{\cos }^{2}x\right)\left(1+{\cot }^{2}x\right)=1[/latex].
Simplify trigonometric expressions using algebra and the identities
We have seen that algebra is very important in verifying trigonometric identities, but it is just as critical in simplifying trigonometric expressions before solving. Being familiar with the basic properties and formulas of algebra, such as the difference of squares formula, the perfect square formula, or substitution, will simplify the work involved with trigonometric expressions and equations.
For example, the equation [latex]\left(\sin x+1\right)\left(\sin x - 1\right)=0[/latex] resembles the equation [latex]\left(x+1\right)\left(x - 1\right)=0[/latex], which uses the factored form of the difference of squares. Using algebra makes finding a solution straightforward and familiar. We can set each factor equal to zero and solve. This is one example of recognizing algebraic patterns in trigonometric expressions or equations.
Another example is the difference of squares formula, [latex]{a}^{2}-{b}^{2}=\left(a-b\right)\left(a+b\right)[/latex], which is widely used in many areas other than mathematics, such as engineering, architecture, and physics. We can also create our own identities by continually expanding an expression and making the appropriate substitutions. Using algebraic properties and formulas makes many trigonometric equations easier to understand and solve.
Example 8: Writing the Trigonometric Expression as an Algebraic Expression
Write the following trigonometric expression as an algebraic expression: [latex]2{\cos }^{2}\theta +\cos \theta -1[/latex].
Example 9: Rewriting a Trigonometric Expression Using the Difference of Squares
Rewrite the trigonometric expression: [latex]4{\cos }^{2}\theta -1[/latex].
Analysis
If this expression were written in the form of an equation set equal to zero, we could solve each factor using the zero factor property. We could also use substitution like we did in the previous problem and let [latex]\cos \theta =x[/latex], rewrite the expression as [latex]4{x}^{2}-1[/latex], and factor [latex]\left(2x - 1\right)\left(2x+1\right)[/latex]. Then replace [latex]x[/latex] with [latex]\cos \theta[/latex] and solve for the angle.
Try It
Rewrite the trigonometric expression: [latex]25 - 9{\sin }^{2}\theta[/latex].
Example 10: Simplify by Rewriting and Using Substitution
Simplify the expression by rewriting and using identities:
[latex]{\csc }^{2}\theta -{\cot }^{2}\theta[/latex]
Try It
Try It
Use algebraic techniques to verify the identity: [latex]\frac{\cos\theta}{1+\sin\theta}=\frac{1-\sin\theta}{\cos\theta}[/latex].
(Hint: Multiply the numerator and denominator on the left side by [latex]1-\sin\theta[/latex]).
Use sum and difference formulas for cosine
Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite the given angle in terms of two angles that have known trigonometric values. We can use the special angles, which we can review in the unit circle shown in Figure 2.
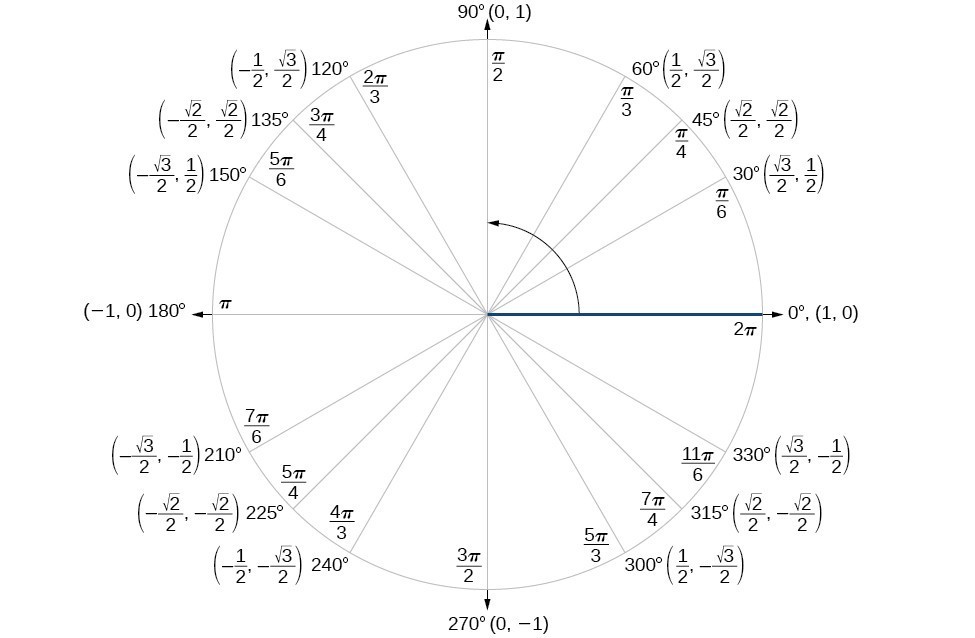
Figure 4. The Unit Circle
We will begin with the sum and difference formulas for cosine, so that we can find the cosine of a given angle if we can break it up into the sum or difference of two of the special angles.
| Sum formula for cosine | [latex]\cos \left(\alpha +\beta \right)=\cos \alpha \cos \beta -\sin \alpha \sin \beta[/latex] |
| Difference formula for cosine | [latex]\cos \left(\alpha -\beta \right)=\cos \alpha \cos \beta +\sin \alpha \sin \beta[/latex] |
First, we will prove the difference formula for cosines. Let’s consider two points on the unit circle. Point [latex]P[/latex] is at an angle [latex]\alpha[/latex] from the positive x-axis with coordinates [latex]\left(\cos \alpha ,\sin \alpha \right)[/latex] and point [latex]Q[/latex] is at an angle of [latex]\beta[/latex] from the positive x-axis with coordinates [latex]\left(\cos \beta ,\sin \beta \right)[/latex]. Note the measure of angle [latex]POQ[/latex] is [latex]\alpha -\beta[/latex].
Label two more points: [latex]A[/latex] at an angle of [latex]\left(\alpha -\beta \right)[/latex] from the positive x-axis with coordinates [latex]\left(\cos \left(\alpha -\beta \right),\sin \left(\alpha -\beta \right)\right)[/latex]; and point [latex]B[/latex] with coordinates [latex]\left(1,0\right)[/latex]. Triangle [latex]POQ[/latex] is a rotation of triangle [latex]AOB[/latex] and thus the distance from [latex]P[/latex] to [latex]Q[/latex] is the same as the distance from [latex]A[/latex] to [latex]B[/latex].
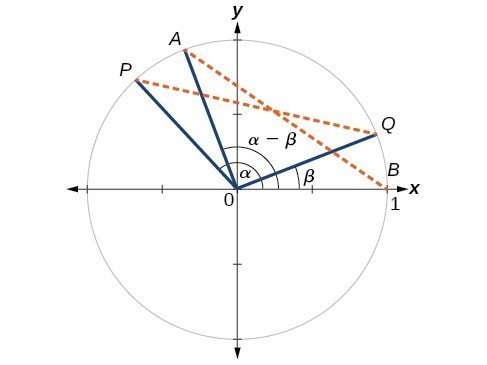
Figure 5. We can find the distance from [latex]P[/latex] to [latex]Q[/latex] using the distance formula.
Then we apply the Pythagorean identity and simplify.
Similarly, using the distance formula we can find the distance from [latex]A[/latex] to [latex]B[/latex].
Applying the Pythagorean identity and simplifying we get:
Because the two distances are the same, we set them equal to each other and simplify.
Finally we subtract [latex]2[/latex] from both sides and divide both sides by [latex]-2[/latex].
Thus, we have the difference formula for cosine. We can use similar methods to derive the cosine of the sum of two angles.
A General Note: Sum and Difference Formulas for Cosine
These formulas can be used to calculate the cosine of sums and differences of angles.
[latex]\begin{align}\cos \left(\alpha +\beta \right)=\cos \alpha \cos \beta -\sin \alpha \sin \beta\end{align}[/latex]
[latex]\begin{align}\cos \left(\alpha -\beta \right)=\cos \alpha \cos \beta +\sin \alpha \sin \beta\end{align}[/latex]
How To: Given two angles, find the cosine of the difference between the angles.
- Write the difference formula for cosine.
- Substitute the values of the given angles into the formula.
- Simplify.
Example 11: Finding the Exact Value Using the Formula for the Cosine of the Difference of Two Angles
Using the formula for the cosine of the difference of two angles, find the exact value of [latex]\cos \left(\frac{5\pi }{4}-\frac{\pi }{6}\right)[/latex].
Try It
Find the exact value of [latex]\cos \left(\frac{\pi }{3}-\frac{\pi }{4}\right)[/latex].
Example 12: Finding the Exact Value Using the Formula for the Sum of Two Angles for Cosine
Find the exact value of [latex]\cos \left({75}^{\circ }\right)[/latex].
Try It
Find the exact value of [latex]\cos \left({105}^{\circ }\right)[/latex].
Try It
Use sum and difference formulas for sine
The sum and difference formulas for sine can be derived in the same manner as those for cosine, and they resemble the cosine formulas.
A General Note: Sum and Difference Formulas for Sine
These formulas can be used to calculate the sines of sums and differences of angles.
[latex]\sin \left(\alpha +\beta \right)=\sin \alpha \cos \beta +\cos \alpha \sin \beta[/latex]
[latex]\sin \left(\alpha -\beta \right)=\sin \alpha \cos \beta -\cos \alpha \sin \beta[/latex]
How To: Given two angles, find the sine of the difference between the angles.
- Write the difference formula for sine.
- Substitute the given angles into the formula.
- Simplify.
Example 13: Using Sum and Difference Identities to Evaluate the Difference of Angles
Use the sum and difference identities to evaluate the difference of the angles and show that part a equals part b.
- [latex]\sin \left({45}^{\circ }-{30}^{\circ }\right)[/latex]
- [latex]\sin \left({135}^{\circ }-{120}^{\circ }\right)[/latex]
Example 14: Finding the Exact Value of an Expression Involving an Inverse Trigonometric Function
Find the exact value of [latex]\sin \left({\cos }^{-1}\frac{1}{2}+{\sin }^{-1}\frac{3}{5}\right)[/latex].
Try It
Use sum and difference formulas for tangent
Finding exact values for the tangent of the sum or difference of two angles is a little more complicated, but again, it is a matter of recognizing the pattern.
Finding the sum of two angles formula for tangent involves taking quotient of the sum formulas for sine and cosine and simplifying. Recall, [latex]\tan x=\frac{\sin x}{\cos x},\cos x\ne 0[/latex].
Let’s derive the sum formula for tangent.
We can derive the difference formula for tangent in a similar way.
A General Note: Sum and Difference Formulas for Tangent
The sum and difference formulas for tangent are:
[latex]\tan \left(\alpha +\beta \right)=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }[/latex]
[latex]\tan \left(\alpha -\beta \right)=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }[/latex]
How To: Given two angles, find the tangent of the sum of the angles.
- Write the sum formula for tangent.
- Substitute the given angles into the formula.
- Simplify.
Example 15: Finding the Exact Value of an Expression Involving Tangent
Find the exact value of [latex]\tan \left(\frac{\pi }{6}+\frac{\pi }{4}\right)[/latex].
Try It
Find the exact value of [latex]\tan \left(\frac{2\pi }{3}+\frac{\pi }{4}\right)[/latex].
Try It
Example 16: Finding Multiple Sums and Differences of Angles
Given [latex]\text{ }\sin \alpha =\frac{3}{5},0<\alpha <\frac{\pi }{2},\cos \beta =-\frac{5}{13},\pi <\beta <\frac{3\pi }{2}[/latex], find
- [latex]\sin \left(\alpha +\beta \right)[/latex]
- [latex]\cos \left(\alpha +\beta \right)[/latex]
- [latex]\tan \left(\alpha +\beta \right)[/latex]
- [latex]\tan \left(\alpha -\beta \right)[/latex]
Now that we can find the sine, cosine, and tangent functions for the sums and differences of angles, we can use them to do the same for their cofunctions. You may recall that if the sum of two positive angles is [latex]\frac{\pi }{2}[/latex], those two angles are complements, and the sum of the two acute angles in a right triangle is [latex]\frac{\pi }{2}[/latex], so they are also complements. In Figure 6, notice that if one of the acute angles is labeled as [latex]\theta[/latex], then the other acute angle must be labeled [latex]\left(\frac{\pi }{2}-\theta \right)[/latex].
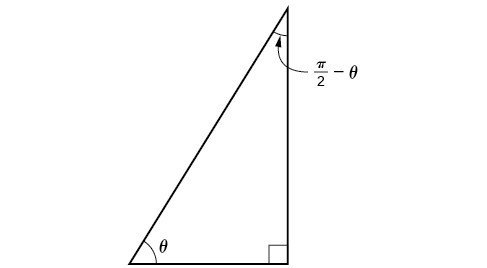
Figure 8. From these relationships, the cofunction identities are formed.
Notice also that [latex]\sin \theta =\cos \left(\frac{\pi }{2}-\theta \right):[/latex] opposite over hypotenuse. Thus, when two angles are complimentary, we can say that the sine of [latex]\theta[/latex] equals the cofunction of the complement of [latex]\theta[/latex]. Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.
A General Note: Cofunction Identities
The cofunction identities are summarized in the table below.
| [latex]\sin \theta =\cos \left(\frac{\pi }{2}-\theta \right)[/latex] | [latex]\cos \theta =\sin \left(\frac{\pi }{2}-\theta \right)[/latex] |
| [latex]\tan \theta =\cot \left(\frac{\pi }{2}-\theta \right)[/latex] | [latex]\cot \theta =\tan \left(\frac{\pi }{2}-\theta \right)[/latex] |
| [latex]\sec \theta =\csc \left(\frac{\pi }{2}-\theta \right)[/latex] | [latex]\csc \theta =\sec \left(\frac{\pi }{2}-\theta \right)[/latex] |
Notice that the formulas in the table may also justified algebraically using the sum and difference formulas. For example, using
we can write
Example 17: Finding a Cofunction with the Same Value as the Given Expression
Write [latex]\tan \frac{\pi }{9}[/latex] in terms of its cofunction.
Try It
Write [latex]\sin \frac{\pi }{7}[/latex] in terms of its cofunction.
Try It
Use sum and difference formulas to verify identities
Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them accessible while working the problems.
How To: Given an identity, verify using sum and difference formulas.
- Begin with the expression on the side of the equal sign that appears most complex. Rewrite that expression until it matches the other side of the equal sign. Occasionally, we might have to alter both sides, but working on only one side is the most efficient.
- Look for opportunities to use the sum and difference formulas.
- Rewrite sums or differences of quotients as single quotients.
- If the process becomes cumbersome, rewrite the expression in terms of sines and cosines.
Example 18: Verifying an Identity Involving Sine
Verify the identity [latex]\sin \left(\alpha +\beta \right)+\sin \left(\alpha -\beta \right)=2\sin \alpha \cos \beta[/latex].
Example 19: Verifying an Identity Involving Tangent
Verify the following identity.
[latex]\frac{\sin \left(\alpha -\beta \right)}{\cos \alpha \cos \beta }=\tan \alpha -\tan \beta[/latex]
Try It
Verify the identity: [latex]\tan \left(\pi -\theta \right)=-\tan \theta[/latex].
Example 20: Using Sum and Difference Formulas to Solve an Application Problem
Let [latex]{L}_{1}[/latex] and [latex]{L}_{2}[/latex] denote two non-vertical intersecting lines, and let [latex]\theta[/latex] denote the acute angle between [latex]{L}_{1}[/latex] and [latex]{L}_{2}[/latex]. Show that
[latex]\tan \theta =\frac{{m}_{2}-{m}_{1}}{1+{m}_{1}{m}_{2}}[/latex]
where [latex]{m}_{1}[/latex] and [latex]{m}_{2}[/latex] are the slopes of [latex]{L}_{1}[/latex] and [latex]{L}_{2}[/latex] respectively. (Hint: Use the fact that [latex]\tan {\theta }_{1}={m}_{1}[/latex] and [latex]\tan {\theta }_{2}={m}_{2}[/latex]. )
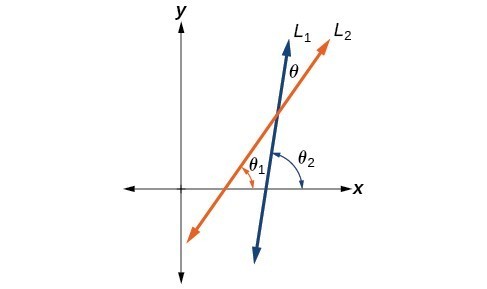
Figure 9
Using Double-Angle Formulas to Find Exact Values
In the previous section, we used addition and subtraction formulas for trigonometric functions. Now, we take another look at those same formulas. The double-angle formulas are a special case of the sum formulas, where [latex]\alpha =\beta[/latex]. Deriving the double-angle formula for sine begins with the sum formula,
If we let [latex]\alpha =\beta =\theta[/latex], then we have
Deriving the double-angle for cosine gives us three options. First, starting from the sum formula, [latex]\cos \left(\alpha +\beta \right)=\cos \alpha \cos \beta -\sin \alpha \sin \beta[/latex], and letting [latex]\alpha =\beta =\theta[/latex], we have
Using the Pythagorean properties, we can expand this double-angle formula for cosine and get two more interpretations. The first one is:
The second interpretation is:
Similarly, to derive the double-angle formula for tangent, replacing [latex]\alpha =\beta =\theta[/latex] in the sum formula gives
A General Note: Double-Angle Formulas
The double-angle formulas are summarized as follows:
[latex]\begin{align}\sin \left(2\theta \right)&=2\sin \theta \cos \theta\\\text{ }\\ \cos \left(2\theta \right)&={\cos }^{2}\theta -{\sin }^{2}\theta \\ &=1 - 2{\sin }^{2}\theta \\ &=2{\cos }^{2}\theta -1 \\\text{ }\\ \tan \left(2\theta \right)&=\frac{2\tan \theta }{1-{\tan }^{2}\theta }\end{align}[/latex]
How To: Given the tangent of an angle and the quadrant in which it is located, use the double-angle formulas to find the exact value.
- Draw a triangle to reflect the given information.
- Determine the correct double-angle formula.
- Substitute values into the formula based on the triangle.
- Simplify.
Example 21: Using a Double-Angle Formula to Find the Exact Value Involving Tangent
Given that [latex]\tan \theta =−\frac{3}{4}[/latex] and [latex]\theta[/latex] is in quadrant II, find the following:
- [latex]\sin \left(2\theta \right)[/latex]
- [latex]\cos \left(2\theta \right)[/latex]
- [latex]\tan \left(2\theta \right)[/latex]
Try It
Given [latex]\sin \alpha =\frac{5}{8}[/latex], with [latex]\theta[/latex] in quadrant I, find [latex]\cos \left(2\alpha \right)[/latex].
Try It
Example 22: Using the Double-Angle Formula for Cosine without Exact Values
Use the double-angle formula for cosine to write [latex]\cos \left(6x\right)[/latex] in terms of [latex]\cos \left(3x\right)[/latex].
Using Double-Angle Formulas to Verify Identities
Establishing identities using the double-angle formulas is performed using the same steps we used to derive the sum and difference formulas. Choose the more complicated side of the equation and rewrite it until it matches the other side.
Example 23: Using the Double-Angle Formulas to Establish an Identity
Establish the following identity using double-angle formulas:
[latex]1+\sin \left(2\theta \right)={\left(\sin \theta +\cos \theta \right)}^{2}[/latex]
Try It
Establish the identity: [latex]{\cos }^{4}\theta -{\sin }^{4}\theta =\cos \left(2\theta \right)[/latex].
Example 24: Verifying a Double-Angle Identity for Tangent
Verify the identity:
[latex]\tan \left(2\theta \right)=\frac{2}{\cot \theta -\tan \theta }[/latex]
Try It
Verify the identity: [latex]\cos \left(2\theta \right)\cos \theta ={\cos }^{3}\theta -\cos \theta {\sin }^{2}\theta[/latex].
Use Reduction Formulas to Simplify an Expression
The double-angle formulas can be used to derive the reduction formulas, which are formulas we can use to reduce the power of a given expression involving even powers of sine or cosine. They allow us to rewrite the even powers of sine or cosine in terms of the first power of cosine. These formulas are especially important in higher-level math courses, calculus in particular. Also called the power-reducing formulas, three identities are included and are easily derived from the double-angle formulas.
We can use two of the three double-angle formulas for cosine to derive the reduction formulas for sine and cosine. Let’s begin with [latex]\cos \left(2\theta \right)=1 - 2{\sin }^{2}\theta[/latex]. Solve for [latex]{\sin }^{2}\theta :[/latex]
Next, we use the formula [latex]\cos \left(2\theta \right)=2{\cos }^{2}\theta -1[/latex]. Solve for [latex]{\cos }^{2}\theta :[/latex]
The last reduction formula is derived by writing tangent in terms of sine and cosine:
A General Note: Reduction Formulas
The reduction formulas are summarized as follows:
[latex]\begin{align}&{\sin }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{2} \\ &{\cos }^{2}\theta =\frac{1+\cos \left(2\theta \right)}{2} \\ &{\tan }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{1+\cos \left(2\theta \right)} \end{align}[/latex]
Example 25: Writing an Equivalent Expression Not Containing Powers Greater Than 1
Write an equivalent expression for [latex]{\cos }^{4}x[/latex] that does not involve any powers of sine or cosine greater than 1.
Example 26: Using the Power-Reducing Formulas to Prove an Identity
Use the power-reducing formulas to prove
[latex]{\sin }^{3}\left(2x\right)=\left[\frac{1}{2}\sin \left(2x\right)\right]\left[1-\cos \left(4x\right)\right][/latex]
Try It
Use the power-reducing formulas to prove that [latex]10{\cos }^{4}x=\frac{15}{4}+5\cos \left(2x\right)+\frac{5}{4}\cos \left(4x\right)[/latex].
Try It
Using Half-Angle Formulas to Find Exact Values
The next set of identities is the set of half-angle formulas, which can be derived from the reduction formulas and we can use when we have an angle that is half the size of a special angle. If we replace [latex]\theta[/latex] with [latex]\frac{\alpha }{2}[/latex], the half-angle formula for sine is found by simplifying the equation and solving for [latex]\sin \left(\frac{\alpha }{2}\right)[/latex]. Note that the half-angle formulas are preceded by a [latex]\pm[/latex] sign. This does not mean that both the positive and negative expressions are valid. Rather, it depends on the quadrant in which [latex]\frac{\alpha }{2}[/latex] terminates.
The half-angle formula for sine is derived as follows:
To derive the half-angle formula for cosine, we have
For the tangent identity, we have
A General Note: Half-Angle Formulas
The half-angle formulas are as follows:
[latex]\begin{align}\sin \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{2}} \\ \text{ } \\ \cos \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1+\cos \alpha }{2}} \\ \text{ } \\ \tan \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }} \\ &=\frac{\sin \alpha }{1+\cos \alpha } \\ &=\frac{1-\cos \alpha }{\sin \alpha }\end{align}[/latex]
Example 27: Using a Half-Angle Formula to Find the Exact Value of a Sine Function
Find [latex]\sin \left({15}^{\circ }\right)[/latex] using a half-angle formula.
How To: Given the tangent of an angle and the quadrant in which the angle lies, find the exact values of trigonometric functions of half of the angle.
- Draw a triangle to represent the given information.
- Determine the correct half-angle formula.
- Substitute values into the formula based on the triangle.
- Simplify.
Example 28: Finding Exact Values Using Half-Angle Identities
Given that [latex]\tan \alpha =\frac{8}{15}[/latex] and [latex]\alpha[/latex] lies in quadrant III, find the exact value of the following:
- [latex]\sin \left(\frac{\alpha }{2}\right)[/latex]
- [latex]\cos \left(\frac{\alpha }{2}\right)[/latex]
- [latex]\tan \left(\frac{\alpha }{2}\right)[/latex]
Try It
Given that [latex]\sin \alpha =-\frac{4}{5}[/latex] and [latex]\alpha[/latex] lies in quadrant IV, find the exact value of [latex]\cos \left(\frac{\alpha }{2}\right)[/latex].
Try It
Example 29: Finding the Measurement of a Half Angle
Now, we will return to the problem posed at the beginning of the section. A bicycle ramp is constructed for high-level competition with an angle of [latex]\theta[/latex] formed by the ramp and the ground. Another ramp is to be constructed half as steep for novice competition. If [latex]\tan \theta =\frac{5}{3}[/latex] for higher-level competition, what is the measurement of the angle for novice competition?
Glossary
Key Equations
| Pythagorean identities | [latex]\begin{gathered}{\sin }^{2}\theta +{\cos }^{2}\theta =1\\ 1+{\cot }^{2}\theta ={\csc }^{2}\theta \\ 1+{\tan }^{2}\theta ={\sec }^{2}\theta \end{gathered}[/latex] |
| Even-odd identities | [latex]\begin{gathered}\tan \left(-\theta \right)=-\tan \theta \\ \cot \left(-\theta \right)=-\cot \theta \\ \sin \left(-\theta \right)=-\sin \theta \\ \csc \left(-\theta \right)=-\csc \theta \\ \cos \left(-\theta \right)=\cos \theta \\ \sec \left(-\theta \right)=\sec \theta \end{gathered}[/latex] |
| Reciprocal identities | [latex]\begin{gathered}\sin \theta =\frac{1}{\csc \theta }\\ \cos \theta =\frac{1}{\sec \theta }\\ \tan \theta =\frac{1}{\cot \theta }\\ \csc \theta =\frac{1}{\sin \theta }\\ \sec \theta =\frac{1}{\cos \theta }\\ \cot \theta =\frac{1}{\tan \theta }\end{gathered}[/latex] |
| Quotient identities | [latex]\begin{gathered} \tan \theta =\frac{\sin \theta }{\cos \theta }\\ \cot \theta =\frac{\cos \theta }{\sin \theta } \end{gathered}[/latex] |
| Sum Formula for Cosine | [latex]\cos \left(\alpha +\beta \right)=\cos \alpha \cos \beta -\sin \alpha \sin \beta[/latex] |
| Difference Formula for Cosine | [latex]\cos \left(\alpha -\beta \right)=\cos \alpha \cos \beta +\sin \alpha \sin \beta[/latex] |
| Sum Formula for Sine | [latex]\sin \left(\alpha +\beta \right)=\sin \alpha \cos \beta +\cos \alpha \sin \beta[/latex] |
| Difference Formula for Sine | [latex]\sin \left(\alpha -\beta \right)=\sin \alpha \cos \beta -\cos \alpha \sin \beta[/latex] |
| Sum Formula for Tangent | [latex]\tan \left(\alpha +\beta \right)=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }[/latex] |
| Difference Formula for Tangent | [latex]\tan \left(\alpha -\beta \right)=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }[/latex] |
| Cofunction identities | [latex]\sin \theta =\cos \left(\frac{\pi }{2}-\theta \right)[/latex]
[latex]\cos \theta =\sin \left(\frac{\pi }{2}-\theta \right)[/latex] [latex]\tan \theta =\cot \left(\frac{\pi }{2}-\theta \right)[/latex] [latex]\cot \theta =\tan \left(\frac{\pi }{2}-\theta \right)[/latex] [latex]\sec \theta =\csc \left(\frac{\pi }{2}-\theta \right)[/latex] [latex]\csc \theta =\sec \left(\frac{\pi }{2}-\theta \right)[/latex] |
| Double-angle formulas | [latex]\begin{align}\sin \left(2\theta \right)&=2\sin \theta \cos \theta\\\text{ }\\ \cos \left(2\theta \right)&={\cos }^{2}\theta -{\sin }^{2}\theta \\ &=1 - 2{\sin }^{2}\theta \\ &=2{\cos }^{2}\theta -1 \\\text{ }\\ \tan \left(2\theta \right)&=\frac{2\tan \theta }{1-{\tan }^{2}\theta }\end{align}[/latex] |
| Reduction formulas | [latex]\begin{align}&{\sin }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{2} \\ &{\cos }^{2}\theta =\frac{1+\cos \left(2\theta \right)}{2} \\ &{\tan }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{1+\cos \left(2\theta \right)} \end{align}[/latex] |
| Half-angle formulas | [latex]\begin{align}\sin \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{2}} \\ \text{ } \\ \cos \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1+\cos \alpha }{2}} \\ \text{ } \\ \tan \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }} \\ &=\frac{\sin \alpha }{1+\cos \alpha } \\ &=\frac{1-\cos \alpha }{\sin \alpha }\end{align}[/latex] |
Key Concepts
- There are multiple ways to represent a trigonometric expression. Verifying the identities illustrates how expressions can be rewritten to simplify a problem.
- Graphing both sides of an identity will verify it.
- Simplifying one side of the equation to equal the other side is another method for verifying an identity.
- The approach to verifying an identity depends on the nature of the identity. It is often useful to begin on the more complex side of the equation.
- We can create an identity by simplifying an expression and then verifying it.
- Verifying an identity may involve algebra with the fundamental identities.
- Algebraic techniques can be used to simplify trigonometric expressions. We use algebraic techniques throughout this text, as they consist of the fundamental rules of mathematics.
- The sum formula for cosines states that the cosine of the sum of two angles equals the product of the cosines of the angles minus the product of the sines of the angles. The difference formula for cosines states that the cosine of the difference of two angles equals the product of the cosines of the angles plus the product of the sines of the angles.
- The sum and difference formulas can be used to find the exact values of the sine, cosine, or tangent of an angle.
- The sum formula for sines states that the sine of the sum of two angles equals the product of the sine of the first angle and cosine of the second angle plus the product of the cosine of the first angle and the sine of the second angle. The difference formula for sines states that the sine of the difference of two angles equals the product of the sine of the first angle and cosine of the second angle minus the product of the cosine of the first angle and the sine of the second angle.
- The sum and difference formulas for sine and cosine can also be used for inverse trigonometric functions.
- The sum formula for tangent states that the tangent of the sum of two angles equals the sum of the tangents of the angles divided by 1 minus the product of the tangents of the angles. The difference formula for tangent states that the tangent of the difference of two angles equals the difference of the tangents of the angles divided by 1 plus the product of the tangents of the angles.
- The Pythagorean Theorem along with the sum and difference formulas can be used to find multiple sums and differences of angles.
- The cofunction identities apply to complementary angles and pairs of reciprocal functions.
- Sum and difference formulas are useful in verifying identities.
- Application problems are often easier to solve by using sum and difference formulas.
- Double-angle identities are derived from the sum formulas of the fundamental trigonometric functions: sine, cosine, and tangent.
- Reduction formulas are especially useful in calculus, as they allow us to reduce the power of the trigonometric term.
- Half-angle formulas allow us to find the value of trigonometric functions involving half-angles, whether the original angle is known or not.
Glossary
- double-angle formulas
- identities derived from the sum formulas for sine, cosine, and tangent in which the angles are equal
even-odd identities
- set of equations involving trigonometric functions such that if [latex]f\left(-x\right)=-f\left(x\right)[/latex], the identity is odd, and if [latex]f\left(-x\right)=f\left(x\right)[/latex], the identity is even
- half-angle formulas
- identities derived from the reduction formulas and used to determine half-angle values of trigonometric functions
Pythagorean identities
- set of equations involving trigonometric functions based on the right triangle properties
quotient identities
- pair of identities based on the fact that tangent is the ratio of sine and cosine, and cotangent is the ratio of cosine and sine
reciprocal identities
- set of equations involving the reciprocals of basic trigonometric definitions
- reduction formulas
- identities derived from the double-angle formulas and used to reduce the power of a trigonometric function
Candela Citations
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution





