Learning Outcomes
By the end of this section, you will be able to:
- Use the Law of Sines to solve oblique triangles.
- Find the area of an oblique triangle using the sine function.
- Solve applied problems using the Law of Sines.
- Use the Law of Cosines to solve oblique triangles.
- Solve applied problems using the Law of Cosines.
- Use Heron’s formula to find the area of a triangle.
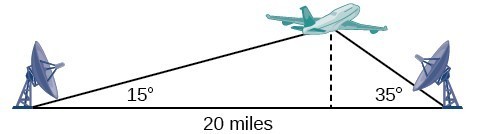
Figure 1
Using the Law of Sines to Solve Obliques Triangles
In any triangle, we can draw an altitude, a perpendicular line from one vertex to the opposite side, forming two right triangles. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles.
Any triangle that is not a right triangle is an oblique triangle. Solving an oblique triangle means finding the measurements of all three angles and all three sides. To do so, we need to start with at least three of these values, including at least one of the sides. We will investigate three possible oblique triangle problem situations:
- ASA (angle-side-angle) We know the measurements of two angles and the included side. See Figure 2.

Figure 2
- AAS (angle-angle-side) We know the measurements of two angles and a side that is not between the known angles. See Figure 3.

Figure 3
- SSA (side-side-angle) We know the measurements of two sides and an angle that is not between the known sides. See Figure 4.

Figure 4
Knowing how to approach each of these situations enables us to solve oblique triangles without having to drop a perpendicular to form two right triangles. Instead, we can use the fact that the ratio of the measurement of one of the angles to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. Let’s see how this statement is derived by considering the triangle shown in Figure 5.
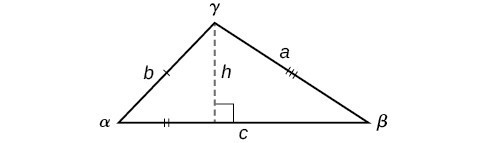
Figure 5
Using the right triangle relationships, we know that [latex]\sin \alpha =\frac{h}{b}[/latex] and [latex]\sin \beta =\frac{h}{a}[/latex]. Solving both equations for [latex]h[/latex] gives two different expressions for [latex]h[/latex].
We then set the expressions equal to each other.
Similarly, we can compare the other ratios.
Collectively, these relationships are called the Law of Sines.
Note the standard way of labeling triangles: angle [latex]\alpha[/latex] (alpha) is opposite side [latex]a[/latex]; angle [latex]\beta[/latex] (beta) is opposite side [latex]b[/latex]; and angle [latex]\gamma[/latex] (gamma) is opposite side [latex]c[/latex]. See Figure 6.
While calculating angles and sides, be sure to carry the exact values through to the final answer. Generally, final answers are rounded to the nearest tenth, unless otherwise specified.
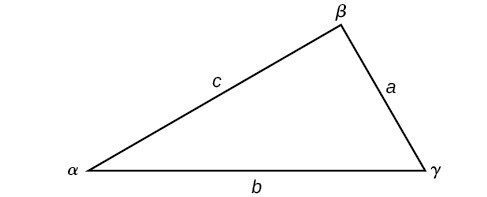
Figure 6
A General Note: Law of Sines
Given a triangle with angles and opposite sides labeled as in Figure 6, the ratio of the measurement of an angle to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. All proportions will be equal. The Law of Sines is based on proportions and is presented symbolically two ways.
[latex]\frac{\sin \alpha }{a}=\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}[/latex]
[latex]\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }[/latex]
To solve an oblique triangle, use any pair of applicable ratios.
Example 1: Solving for Two Unknown Sides and Angle of an AAS Triangle
Solve the triangle shown in Figure 7 to the nearest tenth.
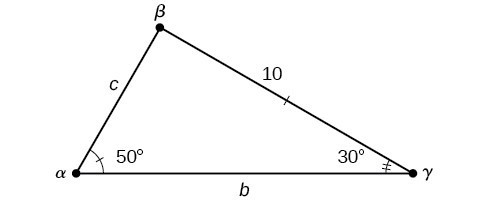
Figure 7
Try It
Solve the triangle shown in Figure 8 to the nearest tenth.
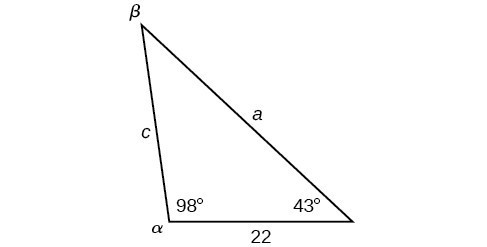
Figure 8
Try It
Using The Law of Sines to Solve SSA Triangles
We can use the Law of Sines to solve any oblique triangle, but some solutions may not be straightforward. In some cases, more than one triangle may satisfy the given criteria, which we describe as an ambiguous case. Triangles classified as SSA, those in which we know the lengths of two sides and the measurement of the angle opposite one of the given sides, may result in one or two solutions, or even no solution.
A General Note: Possible Outcomes for SSA Triangles
Oblique triangles in the category SSA may have four different outcomes. Figure 9 illustrates the solutions with the known sides [latex]a[/latex] and [latex]b[/latex] and known angle [latex]\alpha[/latex].
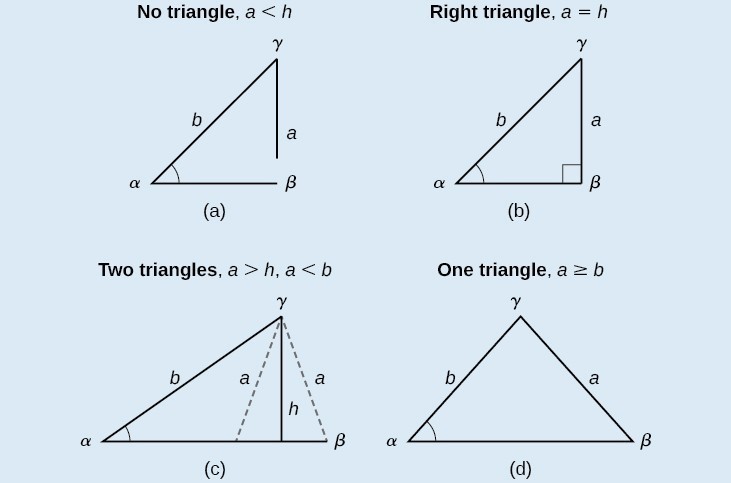
Figure 9
Example 2: Solving an Oblique SSA Triangle
Solve the triangle in Figure 10 for the missing side and find the missing angle measures to the nearest tenth.
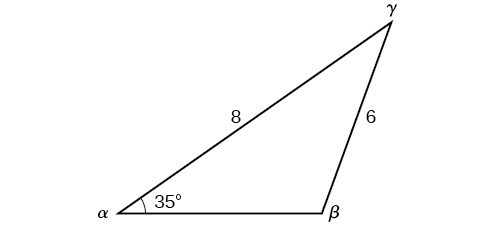
Figure 10
Try It
Given [latex]\alpha =80^\circ ,a=120[/latex], and [latex]b=121[/latex], find the missing side and angles. If there is more than one possible solution, show both.
Example 3: Solving for the Unknown Sides and Angles of a SSA Triangle
In the triangle shown in Figure 13, solve for the unknown side and angles. Round your answers to the nearest tenth.
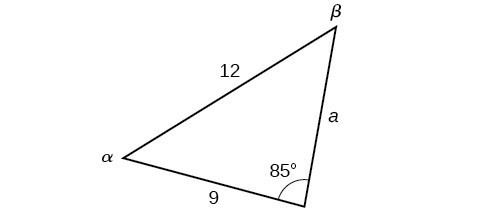
Figure 13
Try It
Given [latex]\alpha =80^\circ ,a=100,b=10[/latex], find the missing side and angles. If there is more than one possible solution, show both. Round your answers to the nearest tenth.
Example 4: Finding the Triangles That Meet the Given Criteria
Find all possible triangles if one side has length 4 opposite an angle of 50°, and a second side has length 10.
Try It
Determine the number of triangles possible given [latex]a=31,b=26,\beta =48^\circ[/latex].
Try It
Finding the Area of an Oblique Triangle Using the Sine Function
Now that we can solve a triangle for missing values, we can use some of those values and the sine function to find the area of an oblique triangle. Recall that the area formula for a triangle is given as [latex]\text{Area}=\frac{1}{2}bh[/latex], where [latex]b[/latex] is base and [latex]h[/latex] is height. For oblique triangles, we must find [latex]h[/latex] before we can use the area formula. Observing the two triangles in Figure 15, one acute and one obtuse, we can drop a perpendicular to represent the height and then apply the trigonometric property [latex]\sin \alpha =\frac{\text{opposite}}{\text{hypotenuse}}[/latex] to write an equation for area in oblique triangles. In the acute triangle, we have [latex]\sin \alpha =\frac{h}{c}[/latex] or [latex]c\sin \alpha =h[/latex]. However, in the obtuse triangle, we drop the perpendicular outside the triangle and extend the base [latex]b[/latex] to form a right triangle. The angle used in calculation is [latex]{\alpha }^{\prime }[/latex], or [latex]180-\alpha[/latex].
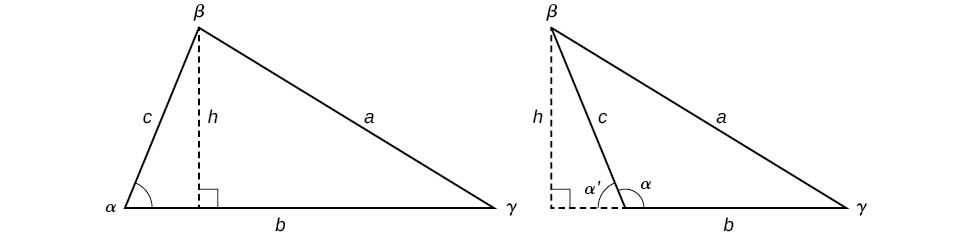
Figure 15
Thus,
Similarly,
A General Note: Area of an Oblique Triangle
The formula for the area of an oblique triangle is given by
[latex]\begin{align}\text{Area}&=\frac{1}{2}bc\sin \alpha \\ &=\frac{1}{2}ac\sin \beta \\ &=\frac{1}{2}ab\sin \gamma \end{align}[/latex]
This is equivalent to one-half of the product of two sides and the sine of their included angle.
Example 5: Finding the Area of an Oblique Triangle
Find the area of a triangle with sides [latex]a=90,b=52[/latex], and angle [latex]\gamma =102^\circ[/latex]. Round the area to the nearest integer.
Try It
Find the area of the triangle given [latex]\beta =42^\circ ,a=7.2\text{ft},c=3.4\text{ft}[/latex]. Round the area to the nearest tenth.
Try It
Solving Applied Problems Using the Law of Sines
The more we study trigonometric applications, the more we discover that the applications are countless. Some are flat, diagram-type situations, but many applications in calculus, engineering, and physics involve three dimensions and motion.
Example 6: Finding an Altitude
Find the altitude of the aircraft in the problem introduced at the beginning of this section, shown in Figure 16. Round the altitude to the nearest tenth of a mile.
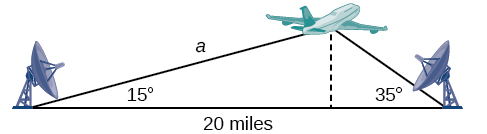
Figure 16
Try It
The diagram shown in Figure 17 represents the height of a blimp flying over a football stadium. Find the height of the blimp if the angle of elevation at the southern end zone, point A, is 70°, the angle of elevation from the northern end zone, point [latex]B[/latex], is 62°, and the distance between the viewing points of the two end zones is 145 yards.
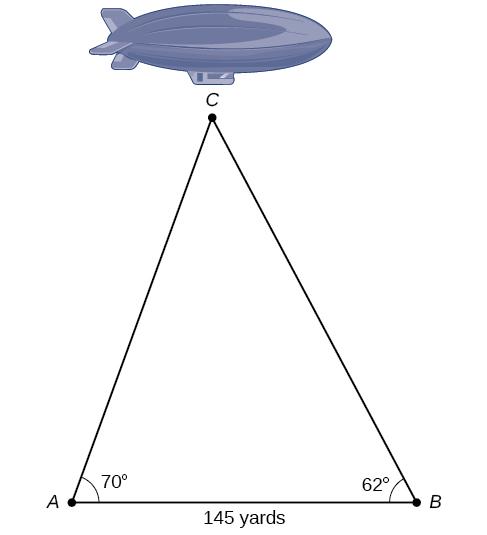
Figure 17
Try It
Suppose a boat leaves port, travels 10 miles, turns 20 degrees, and travels another 8 miles as shown in Figure 1. How far from port is the boat?

Figure 18
Unfortunately, while the Law of Sines enables us to address many non-right triangle cases, it does not help us with triangles where the known angle is between two known sides, a SAS (side-angle-side) triangle, or when all three sides are known, but no angles are known, a SSS (side-side-side) triangle. In this section, we will investigate another tool for solving oblique triangles described by these last two cases.
Using the Law of Cosines to Solve Oblique Triangles
The tool we need to solve the problem of the boat’s distance from the port is the Law of Cosines, which defines the relationship among angle measurements and side lengths in oblique triangles. Three formulas make up the Law of Cosines. At first glance, the formulas may appear complicated because they include many variables. However, once the pattern is understood, the Law of Cosines is easier to work with than most formulas at this mathematical level.
Understanding how the Law of Cosines is derived will be helpful in using the formulas. The derivation begins with the Generalized Pythagorean Theorem, which is an extension of the Pythagorean Theorem to non-right triangles. Here is how it works: An arbitrary non-right triangle [latex]ABC[/latex] is placed in the coordinate plane with vertex [latex]A[/latex] at the origin, side [latex]c[/latex] drawn along the x-axis, and vertex [latex]C[/latex] located at some point [latex]\left(x,y\right)[/latex] in the plane, as illustrated in Figure 2. Generally, triangles exist anywhere in the plane, but for this explanation we will place the triangle as noted.

Figure 19
We can drop a perpendicular from [latex]C[/latex] to the x-axis (this is the altitude or height). Recalling the basic trigonometric identities, we know that
In terms of [latex]\theta ,\text{ }x=b\cos \theta[/latex] and [latex]y=b\sin \theta .\text{ }[/latex] The [latex]\left(x,y\right)[/latex] point located at [latex]C[/latex] has coordinates [latex]\left(b\cos \theta ,b\sin \theta \right)[/latex]. Using the side [latex]\left(x-c\right)[/latex] as one leg of a right triangle and [latex]y[/latex] as the second leg, we can find the length of hypotenuse [latex]a[/latex] using the Pythagorean Theorem. Thus,
The formula derived is one of the three equations of the Law of Cosines. The other equations are found in a similar fashion.
Keep in mind that it is always helpful to sketch the triangle when solving for angles or sides. In a real-world scenario, try to draw a diagram of the situation. As more information emerges, the diagram may have to be altered. Make those alterations to the diagram and, in the end, the problem will be easier to solve.
A General Note: Law of Cosines
The Law of Cosines states that the square of any side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the included angle. For triangles labeled as in Figure 3, with angles [latex]\alpha ,\beta[/latex], and [latex]\gamma[/latex], and opposite corresponding sides [latex]a,b[/latex], and [latex]c[/latex], respectively, the Law of Cosines is given as three equations.
[latex]{a}^{2}={b}^{2}+{c}^{2}-2bc\cos \alpha[/latex]
[latex]{b}^{2}={a}^{2}+{c}^{2}-2ac\cos \beta[/latex]
[latex]{c}^{2}={a}^{2}+{b}^{2}-2ab\cos \gamma[/latex]

Figure 20
To solve for a missing side measurement, the corresponding opposite angle measure is needed.
When solving for an angle, the corresponding opposite side measure is needed. We can use another version of the Law of Cosines to solve for an angle.
[latex]\cos \alpha =\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}[/latex]
[latex]\cos \beta =\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}[/latex]
[latex]\cos\gamma =\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}[/latex]
How To: Given two sides and the angle between them (SAS), find the measures of the remaining side and angles of a triangle.
- Sketch the triangle. Identify the measures of the known sides and angles. Use variables to represent the measures of the unknown sides and angles.
- Apply the Law of Cosines to find the length of the unknown side or angle.
- Apply the Law of Sines or Cosines to find the measure of a second angle.
- Compute the measure of the remaining angle.
Example 7: Finding the Unknown Side and Angles of a SAS Triangle
Find the unknown side and angles of the triangle in Figure 4.

Figure 21
Try It
Find the missing side and angles of the given triangle: [latex]\alpha =30^\circ ,b=12,c=24[/latex].
Try It
Example 8: Solving for an Angle of a SSS Triangle
Find the angle [latex]\alpha[/latex] for the given triangle if side [latex]a=20[/latex], side [latex]b=25[/latex], and side [latex]c=18[/latex].
Try It
Given [latex]a=5,b=7[/latex], and [latex]c=10[/latex], find the missing angles.
Try It
Solving Applied Problems Using the Law of Cosines
Just as the Law of Sines provided the appropriate equations to solve a number of applications, the Law of Cosines is applicable to situations in which the given data fits the cosine models. We may see these in the fields of navigation, surveying, astronomy, and geometry, just to name a few.
Example 9: Using the Law of Cosines to Solve a Communication Problem
On many cell phones with GPS, an approximate location can be given before the GPS signal is received. This is accomplished through a process called triangulation, which works by using the distances from two known points. Suppose there are two cell phone towers within range of a cell phone. The two towers are located 6000 feet apart along a straight highway, running east to west, and the cell phone is north of the highway. Based on the signal delay, it can be determined that the signal is 5050 feet from the first tower and 2420 feet from the second tower. Determine the position of the cell phone north and east of the first tower, and determine how far it is from the highway.
Example 10: Calculating Distance Traveled Using a SAS Triangle
Returning to our problem at the beginning of this section, suppose a boat leaves port, travels 10 miles, turns 20 degrees, and travels another 8 miles. How far from port is the boat? The diagram is repeated here in Figure 8.

Figure 25
Using Heron’s Formula to Find the Area of a Triangle
We already learned how to find the area of an oblique triangle when we know two sides and an angle. We also know the formula to find the area of a triangle using the base and the height. When we know the three sides, however, we can use Heron’s formula instead of finding the height. Heron of Alexandria was a geometer who lived during the first century A.D. He discovered a formula for finding the area of oblique triangles when three sides are known.
A General Note: Heron’s Formula
Heron’s formula finds the area of oblique triangles in which sides [latex]a,b[/latex], and [latex]c[/latex] are known.
[latex]\text{Area}=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}[/latex]
where [latex]s=\frac{\left(a+b+c\right)}{2}[/latex] is one half of the perimeter of the triangle, sometimes called the semi-perimeter.
Example 11: Using Heron’s Formula to Find the Area of a Given Triangle
Find the area of the triangle in Figure 9 using Heron’s formula.

Figure 26
Try It
Use Heron’s formula to find the area of a triangle with sides of lengths [latex]a=29.7\text{ft},b=42.3\text{ft}[/latex], and [latex]c=38.4\text{ft}[/latex].
Try It
Example 12: Applying Heron’s Formula to a Real-World Problem
A Chicago city developer wants to construct a building consisting of artist’s lofts on a triangular lot bordered by Rush Street, Wabash Avenue, and Pearson Street. The frontage along Rush Street is approximately 62.4 meters, along Wabash Avenue it is approximately 43.5 meters, and along Pearson Street it is approximately 34.1 meters. How many square meters are available to the developer? See Figure 10 for a view of the city property.

Figure 27
Try It
Find the area of a triangle given [latex]a=4.38\text{ft},b=3.79\text{ft,}[/latex] and [latex]c=5.22\text{ft}\text{.}[/latex]
Try It
Key Equations
| Law of Sines |
[latex]\frac{\sin \alpha }{a}=\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}[/latex] [latex]\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }[/latex] |
| Area for oblique triangles | [latex]\begin{align}\text{Area}&=\frac{1}{2}bc\sin \alpha \\ &=\frac{1}{2}ac\sin \beta \\ &=\frac{1}{2}ab\sin \gamma \end{align}[/latex] |
| Law of Cosines |
[latex]{a}^{2}={b}^{2}+{c}^{2}-2bc\cos \alpha[/latex] [latex]{b}^{2}={a}^{2}+{c}^{2}-2ac\cos \beta[/latex] [latex]{c}^{2}={a}^{2}+{b}^{2}-2ab\cos \gamma[/latex] |
| Heron’s formula | [latex]\text{Area}=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}[/latex] where [latex]s=\frac{\left(a+b+c\right)}{2}[/latex] |
Key Concepts
- The Law of Sines can be used to solve oblique triangles, which are non-right triangles.
- According to the Law of Sines, the ratio of the measurement of one of the angles to the length of its opposite side equals the other two ratios of angle measure to opposite side.
- There are three possible cases: ASA, AAS, SSA. Depending on the information given, we can choose the appropriate equation to find the requested solution.
- The ambiguous case arises when an oblique triangle can have different outcomes.
- There are three possible cases that arise from SSA arrangement—a single solution, two possible solutions, and no solution.
- The Law of Sines can be used to solve triangles with given criteria.
- The general area formula for triangles translates to oblique triangles by first finding the appropriate height value.
- There are many trigonometric applications. They can often be solved by first drawing a diagram of the given information and then using the appropriate equation.
- The Law of Cosines defines the relationship among angle measurements and lengths of sides in oblique triangles.
- The Generalized Pythagorean Theorem is the Law of Cosines for two cases of oblique triangles: SAS and SSS. Dropping an imaginary perpendicular splits the oblique triangle into two right triangles or forms one right triangle, which allows sides to be related and measurements to be calculated.
- The Law of Cosines is useful for many types of applied problems. The first step in solving such problems is generally to draw a sketch of the problem presented. If the information given fits one of the three models (the three equations), then apply the Law of Cosines to find a solution.
- Heron’s formula allows the calculation of area in oblique triangles. All three sides must be known to apply Heron’s formula.
-
-
Glossary
- altitude
- a perpendicular line from one vertex of a triangle to the opposite side, or in the case of an obtuse triangle, to the line containing the opposite side, forming two right triangles
- ambiguous case
- a scenario in which more than one triangle is a valid solution for a given oblique SSA triangle
- Generalized Pythagorean Theorem
- an extension of the Law of Cosines; relates the sides of an oblique triangle and is used for SAS and SSS triangles
-
- Law of Cosines
- states that the square of any side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the included angle
- Law of Sines
- states that the ratio of the measurement of one angle of a triangle to the length of its opposite side is equal to the remaining two ratios of angle measure to opposite side; any pair of proportions may be used to solve for a missing angle or side
- oblique triangle
- any triangle that is not a right triangle
-
Candela Citations
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution





