1. Define a parabola in terms of its focus and directrix.
2. If the equation of a parabola is written in standard form and [latex]p[/latex] is positive and the directrix is a vertical line, then what can we conclude about its graph?
3. If the equation of a parabola is written in standard form and [latex]p[/latex] is negative and the directrix is a horizontal line, then what can we conclude about its graph?
4. What is the effect on the graph of a parabola if its equation in standard form has increasing values of [latex]p\text{?}[/latex]
5. As the graph of a parabola becomes wider, what will happen to the distance between the focus and directrix?
For the following exercises, determine whether the given equation is a parabola. If so, rewrite the equation in standard form.
6. [latex]{y}^{2}=4-{x}^{2}[/latex]
7. [latex]y=4{x}^{2}[/latex]
8. [latex]3{x}^{2}-6{y}^{2}=12[/latex]
9. [latex]{\left(y - 3\right)}^{2}=8\left(x - 2\right)[/latex]
10. [latex]{y}^{2}+12x - 6y - 51=0[/latex]
For the following exercises, rewrite the given equation in standard form, and then determine the vertex [latex]\left(V\right)[/latex], focus [latex]\left(F\right)[/latex], and directrix [latex]\text{ }\left(d\right)\text{ }[/latex] of the parabola.
11. [latex]x=8{y}^{2}[/latex]
12. [latex]y=\frac{1}{4}{x}^{2}[/latex]
13. [latex]y=-4{x}^{2}[/latex]
14. [latex]x=\frac{1}{8}{y}^{2}[/latex]
15. [latex]x=36{y}^{2}[/latex]
16. [latex]x=\frac{1}{36}{y}^{2}[/latex]
17. [latex]{\left(x - 1\right)}^{2}=4\left(y - 1\right)[/latex]
18. [latex]{\left(y - 2\right)}^{2}=\frac{4}{5}\left(x+4\right)[/latex]
19. [latex]{\left(y - 4\right)}^{2}=2\left(x+3\right)[/latex]
20. [latex]{\left(x+1\right)}^{2}=2\left(y+4\right)[/latex]
21. [latex]{\left(x+4\right)}^{2}=24\left(y+1\right)[/latex]
22. [latex]{\left(y+4\right)}^{2}=16\left(x+4\right)[/latex]
23. [latex]{y}^{2}+12x - 6y+21=0[/latex]
24. [latex]{x}^{2}-4x - 24y+28=0[/latex]
25. [latex]5{x}^{2}-50x - 4y+113=0[/latex]
26. [latex]{y}^{2}-24x+4y - 68=0[/latex]
27. [latex]{x}^{2}-4x+2y - 6=0[/latex]
28. [latex]{y}^{2}-6y+12x - 3=0[/latex]
29. [latex]3{y}^{2}-4x - 6y+23=0[/latex]
30. [latex]{x}^{2}+4x+8y - 4=0[/latex]
For the following exercises, graph the parabola, labeling the focus and the directrix.
31. [latex]x=\frac{1}{8}{y}^{2}[/latex]
32. [latex]y=36{x}^{2}[/latex]
33. [latex]y=\frac{1}{36}{x}^{2}[/latex]
34. [latex]y=-9{x}^{2}[/latex]
35. [latex]{\left(y - 2\right)}^{2}=-\frac{4}{3}\left(x+2\right)[/latex]
36. [latex]-5{\left(x+5\right)}^{2}=4\left(y+5\right)[/latex]
37. [latex]-6{\left(y+5\right)}^{2}=4\left(x - 4\right)[/latex]
38. [latex]{y}^{2}-6y - 8x+1=0[/latex]
39. [latex]{x}^{2}+8x+4y+20=0[/latex]
40. [latex]3{x}^{2}+30x - 4y+95=0[/latex]
41. [latex]{y}^{2}-8x+10y+9=0[/latex]
42. [latex]{x}^{2}+4x+2y+2=0[/latex]
43. [latex]{y}^{2}+2y - 12x+61=0[/latex]
44. [latex]-2{x}^{2}+8x - 4y - 24=0[/latex]
For the following exercises, find the equation of the parabola given information about its graph.
45. Vertex is [latex]\left(0,0\right)[/latex]; directrix is [latex]y=4[/latex], focus is [latex]\left(0,-4\right)[/latex].
46. Vertex is [latex]\left(0,0\right)[/latex]; directrix is [latex]x=4[/latex], focus is [latex]\left(-4,0\right)[/latex].
47. Vertex is [latex]\left(2,2\right)[/latex]; directrix is [latex]x=2-\sqrt{2}[/latex], focus is [latex]\left(2+\sqrt{2},2\right)[/latex].
48. Vertex is [latex]\left(-2,3\right)[/latex]; directrix is [latex]x=-\frac{7}{2}[/latex], focus is [latex]\left(-\frac{1}{2},3\right)[/latex].
49. Vertex is [latex]\left(\sqrt{2},-\sqrt{3}\right)[/latex]; directrix is [latex]x=2\sqrt{2}[/latex], focus is [latex]\left(0,-\sqrt{3}\right)[/latex].
50. Vertex is [latex]\left(1,2\right)[/latex]; directrix is [latex]y=\frac{11}{3}[/latex], focus is [latex]\left(1,\frac{1}{3}\right)[/latex].
For the following exercises, determine the equation for the parabola from its graph.
51.
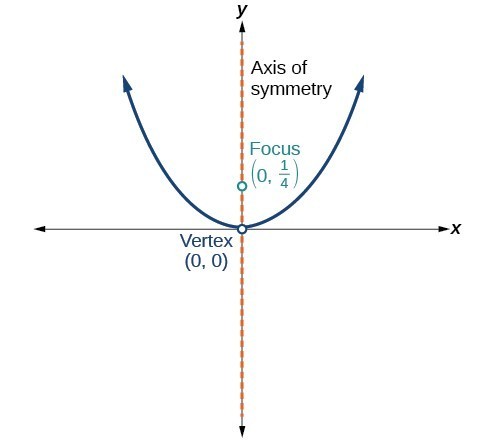
52.

53.

54.

55.

For the following exercises, the vertex and endpoints of the latus rectum of a parabola are given. Find the equation.
56. [latex]V\left(0,0\right),\text{Endpoints }\left(2,1\right),\left(-2,1\right)[/latex]
57. [latex]V\left(0,0\right),\text{Endpoints }\left(-2,4\right),\left(-2,-4\right)[/latex]
58. [latex]V\left(1,2\right),\text{Endpoints }\left(-5,5\right),\left(7,5\right)[/latex]
59. [latex]V\left(-3,-1\right),\text{Endpoints }\left(0,5\right),\left(0,-7\right)[/latex]
60. [latex]V\left(4,-3\right),\text{Endpoints }\left(5,-\frac{7}{2}\right),\left(3,-\frac{7}{2}\right)[/latex]
61. The mirror in an automobile headlight has a parabolic cross-section with the light bulb at the focus. On a schematic, the equation of the parabola is given as [latex]{x}^{2}=4y[/latex]. At what coordinates should you place the light bulb?
62. If we want to construct the mirror from the previous exercise such that the focus is located at [latex]\left(0,0.25\right)[/latex], what should the equation of the parabola be?
63. A satellite dish is shaped like a paraboloid of revolution. This means that it can be formed by rotating a parabola around its axis of symmetry. The receiver is to be located at the focus. If the dish is 12 feet across at its opening and 4 feet deep at its center, where should the receiver be placed?
64. Consider the satellite dish from the previous exercise. If the dish is 8 feet across at the opening and 2 feet deep, where should we place the receiver?
65. A searchlight is shaped like a paraboloid of revolution. A light source is located 1 foot from the base along the axis of symmetry. If the opening of the searchlight is 3 feet across, find the depth.
66. If the searchlight from the previous exercise has the light source located 6 inches from the base along the axis of symmetry and the opening is 4 feet, find the depth.
67. An arch is in the shape of a parabola. It has a span of 100 feet and a maximum height of 20 feet. Find the equation of the parabola, and determine the height of the arch 40 feet from the center.
68. If the arch from the previous exercise has a span of 160 feet and a maximum height of 40 feet, find the equation of the parabola, and determine the distance from the center at which the height is 20 feet.
69. An object is projected so as to follow a parabolic path given by [latex]y=-{x}^{2}+96x[/latex], where [latex]x[/latex] is the horizontal distance traveled in feet and [latex]y[/latex] is the height. Determine the maximum height the object reaches.
70. For the object from the previous exercise, assume the path followed is given by [latex]y=-0.5{x}^{2}+80x[/latex].
Determine how far along the horizontal the object traveled to reach maximum height.
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution. License Terms: Download for free at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface