Write the equation of the line given the slope and the y-intercept using the slope-intercept form
Write the equation of the line given the slope and a point on the line using the point-slope form
Write the equation of the line given two points on the line
Write the equation of a horizontal or vertical line when given the graph
Write the equation of a line given a point and a parallel or perpendicular line
In this section, we will write the equation of a line given some information about the line. We will use two forms of a line to help us do this.
The Slope-Intercept Form: [latex]y = mx + b[/latex]
The Point-Slope Form: [latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]
Write the equation of a line given the slope and y-intercept
In a previous section, we were introduced to the Slope-Intercept Form of a line. We learned that if an equation is written in this form, it is easy to identify the slope of the line and its y-intercept. In this section, we are being asked to write the equation of the line. If we know the slope and the y-intercept of a line, we can use the Slope-Intercept Form to help us do that.
[latex]y = mx + b[/latex]
[latex]\begin{array}{l}\,\,\,\,\,m\,\,\,\,=\,\,\,\text{slope}\\(x,y)=\,\,\,\text{a point on the line}\\\,\,\,\,\,\,\,b\,\,\,\,=\,\,\,\text{the y value of the y-intercept}\end{array}[/latex]
Example 1
Write the equation of the line that has a slope of [latex] \displaystyle \frac{1}{2}[/latex] and a y-intercept of [latex](0,-5)[/latex].
Show Solution
Substitute the slope (m) into [latex]y=mx+b[/latex].
[latex] \displaystyle y=\frac{1}{2}x+b[/latex]
Substitute the y-intercept (b) into the equation.
[latex] \displaystyle y=\frac{1}{2}x-5[/latex]
Answer
[latex]y=\frac{1}{2}x-5[/latex]
We can also find the equation by looking at a graph and finding the slope and y-intercept.
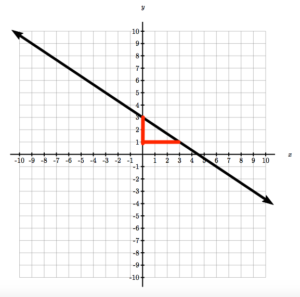
Example 2
Write the equation of the line in the graph by identifying the slope and y-intercept.
Show Solution
Identify the point where the graph crosses the y-axis [latex](0,3)[/latex]. This means the y-intercept is (0,3).
Identify one other point and draw a slope triangle to find the slope.
The slope is [latex]\frac{-2}{3}[/latex]
Substitute the slope and y value of the intercept into the slope-intercept equation.
Write the equation of a line given the slope and a point on the line
Using the slope-intercept form of a line is easy when you know both the slope (m) and the y-intercept (b), but what if you know the slope and just any point on the line, not specifically the y-intercept? Can you still write the equation? The answer is yes, but you will need to put in a little more thought and work than you did previously.
Point-Slope Form
[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]
[latex]\begin{array}{l}\,\,\,\,\,m\,\,\,\,=\,\,\,\text{slope}\\\left({x}_{1},{y}_{1}\right)=\,\,\,\text{a point on the line}\end{array}[/latex]
This is an important formula, as it will be used in other algebra courses and often in calculus to find the equation of a tangent line. We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.
Point-Slope Form
Given a point [latex]\left({x}_{1},{y}_{1}\right)[/latex] and slope m, point-slope form will give the following equation of a line:
[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]
In our first example, we are given the slope and a point on a line. We will use the Point-Slope Form to write the equation of the line.
Example 3
Write the equation of the line with slope [latex]m=-3[/latex] that passes through the point [latex]\left(4,8\right)[/latex]. Write the final equation in slope-intercept form.
Show Solution
Using point-slope form, substitute [latex]-3[/latex] for m and the point [latex]\left(4,8\right)[/latex] for [latex]\left({x}_{1},{y}_{1}\right)[/latex].
[latex]\begin{array}{l}y-{y}_{1}=m\left(x-{x}_{1}\right)\hfill \\ y - 8=-3\left(x - 4\right)\hfill \\ y - 8=-3x+12\hfill \\ y=-3x+20\hfill \end{array}[/latex]
Note that any point on the line can be used to find the equation. If done correctly, the same final equation will be obtained.
The following video shows how to write the equation for a line given its slope and a point on the line.
Think about it
There is an alternate method to finding the equation of a line given a point and a slope. See the example below.
Write the equation of the line that has a slope of 3 and contains the point [latex](1,4)[/latex].
Show Solution
Recall that a point is an (x, y) coordinate pair and that all points on the line will satisfy the linear equation. So, if you have a point on the line, it must be a solution to the equation. Although you don’t know the exact equation yet, you know that you can express the line in slope-intercept form, [latex]y=mx+b[/latex].
You do know the slope (m), but you just don’t know the value of the y-intercept (b). Since point (x, y) is a solution to the equation, you can substitute its coordinates for x and y in [latex]y=mx+b[/latex] and solve to find b!
Substitute the slope (m) into [latex]y=mx+b[/latex].
[latex]y=3x+b[/latex]
Substitute the point [latex](1,4)[/latex] for x and y.
Rewrite [latex]y=mx+b[/latex] with [latex]m=3[/latex] and [latex]b=1[/latex].
Answer
[latex]y=3x+1[/latex]
To confirm our algebra, you can check by graphing the equation [latex]y=3x+1[/latex]. The equation checks because when graphed it passes through the point [latex](1,4)[/latex].
The following video gives an example of this alternate method.
Write the equation of a line given two points on the line
Let’s suppose you don’t know either the slope or the y-intercept, but you do know the location of two points on the line. It is more challenging, but you can find the equation of the line that would pass through those two points. We will begin by using the two points to find the slope of the line. Once you know the slope of the line, you can use the slope and one of the points in the Point-Slope Form to write the equation of the line.
Example 4
Find the equation of the line that passes through the points [latex]\left(3,4\right)[/latex] and [latex]\left(0,-3\right)[/latex]. Write the final equation in slope-intercept form.
Show Solution
First, we calculate the slope using the slope formula and two points.
The easiest way to solve this problem is to recognize that the second point given, [latex](0,-3)[/latex], is in fact the [latex]y[/latex]-intercept. This means we know that [latex]b=-3[/latex] in the slope-intercept form, [latex]y=mx+b[/latex]. Plugging this value in along with the slope gives the desired equation.
[latex]y=mx+b[/latex]
[latex]y=\dfrac{7}{3}x-3[/latex]
Exploring Further
Although we have now answered the question, we now use point-slope form to verify that this will produce the same answer. With the slope of [latex]\dfrac{7}{3}[/latex], we can use either point. Let us pick the point [latex]\left(3,4\right)[/latex] for [latex]\left({x}_{1},{y}_{1}\right)[/latex].
[latex]\begin{array}{l}y - 4=\dfrac{7}{3}\left(x - 3\right)\hfill \\ y - 4=\dfrac{7}{3}x - 7\hfill&\text{Distribute the }\dfrac{7}{3}.\hfill \\ y=\dfrac{7}{3}x - 3\hfill \end{array}[/latex]
In slope-intercept form, the equation is written as [latex]y=\dfrac{7}{3}x - 3[/latex].
This matches the result we arrived at earlier.
Answer
[latex]y=\dfrac{7}{3}x-3[/latex]
In the next example, we again look for the equation of a line given two points. However, this time we are not given the [latex]y[/latex]-intercept.
Example 5
Write the equation of the line that passes through the points [latex](2,1)[/latex] and [latex](−1,−5)[/latex]. Write the equation in slope-intercept form.
Next, we plug this into point-slope form along with either point. Let us use the point [latex](2,1)[/latex] for [latex](x_1,y_1)[/latex]. Then, we solve for [latex]y[/latex].
Let us take this opportunity to confirm our claim that we can use either point in the point-slope form. With the slope we found earlier, this time we use the point [latex](-1,-5)[/latex] for [latex](x_1,y_1)[/latex].
By converting to slope-intercept form, this verifies that either point (and in fact, any point on the line) will produce the same result.
Answer
[latex]y=2x-3[/latex]
To further support that all the ideas we have presented will yield the same result, we now redo the same problem from Example 5 using the “alternate method” presented earlier in this section.
Example 6
Write the equation of the line that passes through the points [latex](2,1)[/latex] and [latex](−1,−5)[/latex]. Write the equation in slope-intercept form.
Rewrite [latex]y=mx+b[/latex] with [latex]m=2[/latex] and [latex]b=-3[/latex].
[latex]y=2x-3[/latex]
Note that this matches the answer we obtained using point-slope form in Example 5.
Answer
[latex]y=2x-3[/latex]
Notice that is doesn’t matter which point you use when you substitute and solve for b—you get the same result for b either way. In the example above, you substituted the coordinates of the point (2, 1) in the equation [latex]y=2x+b[/latex]. Let’s start with the same equation, [latex]y=2x+b[/latex], but substitute in [latex](−1,−5)[/latex]:
In the equation above, [latex]m=1[/latex]. Therefore, the slope is 1.
To find the slope of a parallel line, use the same slope.
The slope of the parallel line is 1.
Use the method for writing an equation from the slope and a point on the line. We will use the Point-Slope Form and substitute 1 for m, and the point [latex](−2,1)[/latex] for [latex]\left({x}_{1},{y}_{1}\right)[/latex] .
Write the equation of a line given a point and a perpendicular line
When you are working with perpendicular lines, you will usually be given one of the lines and an additional point. Remember that two non-vertical lines are perpendicular if the slope of one is the negative reciprocal of the slope of the other. To find the slope of a perpendicular line, find the reciprocal, and then find the opposite of this reciprocal. In other words, flip it and change the sign.
Example 8
Write the equation of a line that contains the point [latex](1,5)[/latex] and is perpendicular to the line [latex]y=2x– 6[/latex].
Show Solution
Identify the slope of the line you want to be perpendicular to.
The given line is written in [latex]y=mx+b[/latex] form, with [latex]m=2[/latex] and [latex]b=-6[/latex]. The slope is 2.
To find the slope of a perpendicular line, find the reciprocal, [latex] \displaystyle \frac{1}{2}[/latex], then the opposite, [latex] \displaystyle -\frac{1}{2}[/latex].
The slope of the perpendicular line is [latex] \displaystyle -\frac{1}{2}[/latex].
For practice, this time, we will use the alternate method for finding the equation of a line. Substitute [latex] \displaystyle -\frac{1}{2}[/latex] for [latex]m[/latex], and the point [latex](1,5)[/latex] for [latex]x[/latex] and [latex]y[/latex] into slope-intercept form.
Write the equation using the new slope for [latex]m[/latex] and the [latex]b[/latex] you just found.
[latex]y=mx+b[/latex]
[latex]y=-\dfrac{1}{2}x+\frac{11}{2}[/latex]
Note, we could have used point-slope form to produce this same result as well. You are encouraged to verify this.
Answer
[latex]y=-\frac{1}{2}x+\frac{11}{2}[/latex]
Video: Write the equation of a line given a point and a perpendicular line (Alternate Method)
Write the equations of lines parallel and perpendicular to horizontal and vertical lines
Example 9
Write the equation of a line that is parallel to the line [latex]y=4[/latex] through the point [latex](0,10)[/latex].
Show Solution
Rewrite the line into [latex]y=mx+b[/latex] form, if needed.
You may notice without doing this that [latex]y=4[/latex] is a horizontal line 4 units above the x-axis. Because it is horizontal, you know its slope is zero.
In the equation above, [latex]m=0[/latex] and [latex]b=4[/latex].
Since [latex]m=0[/latex], the slope is 0. This is a horizontal line.
To find the slope of a parallel line, use the same slope.
The slope of the parallel line is also 0.
Since the parallel line will be a horizontal line, its form is
[latex]y=\text{a constant}[/latex]
Since we want this new line to pass through the point [latex](0,10)[/latex], we will need to write the equation of the new line as:
[latex]y=10[/latex]
This line is parallel to [latex]y=4[/latex] and passes through [latex](0,10)[/latex].
Answer
[latex]y=10[/latex]
Example 10
Write the equation of a line that is perpendicular to the line [latex]y=-3[/latex] through the point [latex](-2,5)[/latex].
Show Solution
In the equation above, [latex]m=0[/latex] and [latex]b=-3[/latex].
A perpendicular line will have a slope that is the negative reciprocal of the slope of [latex]y=-3[/latex], but what does that mean in this case?
The reciprocal of 0 is [latex]\frac{1}{0}[/latex], but we know that dividing by 0 is undefined.
This means that we are looking for a line whose slope is undefined, and we also know that vertical lines have slopes that are undefined. This makes sense since we started with a horizontal line.
The form of a vertical line is [latex]x=\text{a constant}[/latex], where every x-value on the line is equal to some constant. Since we are looking for a line that goes through the point [latex](-2,5)[/latex], all of the x-values on this line must be [latex]-2[/latex].
The equation of a line passing through [latex](-2,5)[/latex] that is perpendicular to the horizontal line [latex]y=-3[/latex] is therefore,
[latex]x=-2[/latex]
Answer
[latex]x=-2[/latex]
Summary
The slope-intercept form of a linear equation is written as [latex]y=mx+b[/latex], where m is the slope and b is the value of y at the y-intercept, which can be written as [latex](0,b)[/latex]. When you know the slope and the y-intercept of a line you can use the slope-intercept form to immediately write the equation of that line. The point-slope form, [latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex], can be used to write the equation of a line when you know the slope and a point on the line or when you know two points on the line.
When lines in a plane are parallel (that is, they never cross), they have the same slope. When lines are perpendicular (that is, they cross at a 90° angle), their slopes are opposite reciprocals of each other. The product of their slopes will be [latex]-1[/latex], except in the case where one of the lines is vertical causing its slope to be undefined. You can use these relationships to find an equation of a line that goes through a particular point and is parallel or perpendicular to another line.
Licenses and Attributions
CC licensed content, Shared previously
Ex: Find the Equation of a Line in Point Slope and Slope Intercept Form Given the Slope and a Point. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/vut5b2fRQQ0. License: CC BY: Attribution
Ex: Find The Equation of the Line in Point-Slope and Slope Intercept Form Given Two Points. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/ndRpJxdmZJI. License: CC BY: Attribution
College Algebra. Provided by: OpenStax. Located at: . License: CC BY: Attribution. License Terms: Download for free: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface
