The way a river flows depends on many variables including how big the river is, how much water it contains, what sorts of things are floating in the river, whether or not it is raining, and so forth. If you want to best describe its flow, you must take into account these other variables. A system of linear equations can help with that.

A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. You will find systems of equations in every application of mathematics. They are a useful tool for discovering and describing how behaviors or processes are interrelated. It is rare to find, for example, a pattern of traffic flow that is only affected by weather. Accidents, time of day, and major sporting events are just a few of the other variables that can affect the flow of traffic in a city. In this section, we will explore some basic principles for graphing and describing the intersection of two lines that make up a system of equations.

Solving a system of linear equations

In this module, we will look at systems of linear equations and inequalities in two variables.  First, we will practice graphing two equations on the same set of axes.  Later we will explore the different considerations you need to make when graphing two linear inequalities on the same set of axes. The same techniques are used to graph a system of linear equations as you have used to graph single linear equations. We can use tables of values, slope and y-intercept, and/or x– and y-intercepts to graph both lines on the same set of axes.

For example, consider the following system of linear equations in two variables.

Let’s graph these using slope-intercept form on the same set of axes. Remember that slope-intercept form looks like [latex]y=mx+b[/latex],  so we will want to solve both equations for [latex]y[/latex].

First, solve for y in [latex]2x+y=-8[/latex]

[latex]\begin{array}{c}2x+y=-8\\ y=-2x - 8\end{array}[/latex]

The system is now written as

[latex]\begin{array}{c}y=-2x - 8\\y=x+1\end{array}[/latex]

Now you can graph both equations using their slopes and intercepts on the same set of axes, as seen in the figure below. Note how the graphs share one point in common. This is their point of intersection, a point that lies on both of the lines.

The solution to the system of equations should be written as the ordered pair (-3, -2). 

Determine whether an ordered pair is a solution for a system of linear equations

Using algebra, we can verify that this shared point is actually [latex]\left(-3,-2\right)[/latex] and not [latex]\left(-2.999,-1.999\right)[/latex]. By substituting the x– and y-values of the ordered pair into the equation of each line, you can test whether the point is on both lines. If the substitution results in a true statement in both equations in the system, then you have found a solution to the system of equations!

Since the solution of the system must be a solution to all the equations in the system, you will need to check the point in each equation. In the following example, we will substitute -3 for x and -2 for y in each equation to test whether it is actually the solution.

Remember that in order to be a solution to the system of equations, the values of the point must be a solution for both equations. Once you find one equation for which the point is false, you have determined that it is not a solution for the system.

In the following video, you will see a system of equations solved by graphing using x and y-intercepts. Notice he mentions that when x and y-intercepts are fractions, our graph may not always be precise enough, so it’s important to verify the solution that is found afterward. If the solution doesn’t satisfy the system, graphing using the slope and y-intercept might give a more accurate graph than using x and y-intercepts.

In the previous examples, we saw lines that crossed at one point. What happens if the two lines never cross?  In the following example, you will be given a system to graph that consists of two parallel lines.

Example 3

Graph the system [latex]\begin{array}{c}y=2x+1\\y=2x-3\end{array}[/latex] using the slopes and y-intercepts of the lines.

Show Solution

First, graph [latex]y=2x+1[/latex] using the slope m = 2 and the y-intercept (0,1)

Next, add [latex]y=2x-3[/latex] using the slope m = 2, and the y-intercept (0,-3)

Notice how these are parallel lines, and they don’t cross.  In the next section we will discuss how there are no solutions to a system of equations that are parallel lines.

In the next example, you will be given a system whose equations look different, but after graphing, turn out to be the same line.

Example 4

Graph the system [latex]\begin{array}{c}y=\frac{1}{2}x+2\\2y-x=4\end{array}[/latex] using the x – and y-intercepts.

Show Solution

First, find the x- and y- intercepts of [latex]y=\frac{1}{2}x+2[/latex]

The x-intercept will have a value of 0 for y, so substitute y=0 into the equation, and isolate the variable x.

[latex]\begin{array}{c}0=\frac{1}{2}x+2\\\underline{-2\,\,\,\,\,\,\,\,\,-2}\\-2=\frac{1}{2}x\\\left(2\right)\left(-2\right)=\left(2\right)\frac{1}{2}x\\-4=x\end{array}[/latex]

The x-intercept of [latex]y=\frac{1}{2}x+2[/latex] is [latex]\left(-4,0\right)[/latex].

The y-intercept is easier to find since this equation is in slope-intercept form.  The y-intercept is (0,2).

Now we can plot [latex]y=\frac{1}{2}x+2[/latex] using the intercepts

Now find the intercepts of [latex]2y-x=4[/latex]

Substitute y = 0 in to the equation to find the x-intercept.

[latex]\begin{array}{c}2y-x=4\\2\left(0\right)-x=4\\x=-4\end{array}[/latex]

The x-intercept of [latex]2y-x=4[/latex] is [latex]\left(-4,0\right)[/latex].

Now substitute x = 0 into the equation to find the y-intercept.

[latex]\begin{array}{c}2y-x=4\\2y-0=4\\2y=4\\y=2\end{array}[/latex]

The y-intercept of [latex]2y-x=4[/latex] is [latex]\left(0,2\right)[/latex].

WAIT, these are the same intercepts as [latex]y=\frac{1}{2}x+2[/latex]!  In fact, [latex]y=\frac{1}{2}x+2[/latex]and [latex]2y-x=4[/latex] are really the same equation, expressed in different ways.  If you were to write them both in slope-intercept form you would see that they are the same equation.

When you graph them, they are the same line. In the next section, we will see that systems with the same two equations in them have an infinite number of solutions.

Use a graph to classify solutions to systems

Recall that a linear equation in two variables graphs as a line, which indicates that all of the points on the line are solutions to that linear equation. There are an infinite number of solutions. As we saw in the last section, if you have a system of linear equations that intersect at one point, this point is a solution to the system.  What happens if the lines never cross, as in the case of distinct parallel lines?  How would you describe the solutions to that kind of system?  In this section, we will explore the three possible outcomes for solutions to a system of linear equations.

Three possible outcomes for solutions to systems of equations

Recall that the solution for a system of equations is the value or values that are true for all equations in the system. There are three possible outcomes for solutions to systems of linear equations.  The graphs of equations within a system can tell you how many solutions exist for that system. Look at the images below. Each shows two lines that make up a system of equations.

One Solution	No Solutions	Infinite Solutions
If the graphs of the equations intersect at exactly one point, then there is one solution that is true for both equations.	If the graphs of the equations do not intersect (if they are distinct parallel lines), then there are no solutions that are true for both equations.	If the graphs of the equations are the same, then there are an infinite number of solutions that are true for both equations.

• One Solution: When a system of equations intersects at exactly one ordered pair, the system has one solution.
• No Solution: When the lines that make up a system are parallel and distinct, there are no solutions because the two lines share no points in common.
• Infinite Solutions: Sometimes the two equations will graph as the same line, in which case we have an infinite number of solutions.

We can further classify systems of two linear equations in two variables using the following terminology:

If you have the opportunity to continue your study of systems of equations, you will discover that with more equations and/or more variables, the idea of a dependent system can become much more complex.  In general, it means that one equation of the system can be obtained by taking constant multiples and sums of other equations in the system. This is worth mentioning here since even with our dependent system, the equations often do not appear the same initially.  Usually one equation will, however, be a constant times the other equation, which results in two different representations of the same line.

Example 5

Using the graph of [latex]\begin{array}{r}y=x\\x+2y=6\end{array}[/latex], shown below, determine how many solutions the system has. Label the system as consistent or inconsistent and independent or dependent.

Show Solution

The lines intersect at one point. So the two lines have only one point in common, there is only one solution to the system.

Since there is at least one solution, the system is consistent.

Since the lines are distinct, the system is independent.

Answer

There is one solution to this system.  The system is consistent and independent.

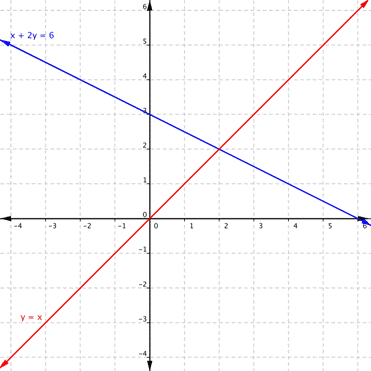
Example 6

Using the graph of [latex]\begin{array}{r}y=3.5x+0.25\\14x–4y=-4.5\end{array}[/latex], shown below, determine how many solutions the system has. Label the system as consistent or inconsistent and independent or dependent.

Show Solution

The lines are parallel and distinct, meaning they do not intersect. There are no solutions to the system.

Since there are no solution, the system is inconsistent.

Since the lines are distinct, the system is independent.

Answer

There are no solutions to the system. The system is inconsistent and independent.

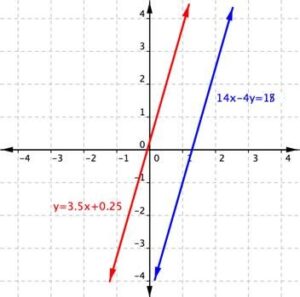
Example 7

How many solutions does the system [latex]\begin{array}{r}y=2x+1\\−4x+2y=2\end{array}[/latex] have? Label the system as consistent or inconsistent and independent or dependent.

Show Solution

First, graph both equations on the same axes.

The two equations graph as the same line. So every point on that line is a solution for the system of equations, implying there are an infinite number of solutions.

Since there is at least one solution, the system is consistent.

Since the lines are collinear, the system is dependent.

Answer

There are an infinite number of solutions. The system is consistent and dependent.

Use a graph to solve a system of equations

Now let us use the skills we have developed to solve a system of equation graphically.  Graphing a system of linear equations consists of choosing which graphing method you want to use and drawing the graphs of both equations on the same set of axes. We now know a solution would be a point where the lines intersect. Our goal is to give all such points, if any exist.

Example 8

Use the graph of [latex]\begin{array}{r}y=x\\x+2y=6\end{array}[/latex], shown below, to solve the system of equations.

Show Solution

We saw this graph in an earlier example, where we determined that the lines intersect at one point, forming a consistent, independent system. Now we want to give the solution to the system.

The point of intersection appears to be the ordered pair [latex]\left(2,2\right)[/latex].  We can check this answer in each equation.

[latex]\hspace{3.05in} y=x \hspace{1.29in} x+2y=6 \\ \hspace{3.05in} 2=2 \hspace{1.18in} 2+2(2)=6 \\ \hspace{3in} TRUE \hspace{1.66in} 6=6 \\ \hspace{4.95in} TRUE [/latex]

This verifies that [latex](2,2)[/latex] is the solution to the system.

Answer

The solution is [latex](2,2)[/latex].

 

Next, we try a system in which we must first graph the lines ourselves.

Example 9

Solve the system of equations graphically.

[latex]\begin{array}{r}x-2y=8\\ y=-2x+6\end{array}[/latex]

Show Solution

First we graph the two lines. You can do this by plotting points, using the x- and y-intercepts, or the slope and y-intercept. For example, with the first equation in standard form, we can quickly find the intercepts. Substituting [latex]y=0[/latex] produces an x-intercept of [latex](8,0)[/latex], while substituting [latex]x=0[/latex] gives a y-intercept of [latex](0,-4)[/latex]. With the second equation being in slope-intercept form, we can graph it using the slope of [latex]m=-2[/latex] and y-intercept [latex](0,6)[/latex]. However, we obtain the graph below.

From the graph, we speculate that the solution is [latex](4,-2)[/latex]. Let us verify this by substituting into the original equations.

[latex]\hspace{3.05in} x-2y=8 \hspace{1.29in} y=-2x+6 \\ \hspace{2.77in} 4-2(-2)=8 \hspace{1.08in} -2=-2(4)+6 \\ \hspace{3.47in} 8=8 \hspace{1.06in} -2=-2 \\ \hspace{3.17in} TRUE \hspace{1.5in} TRUE [/latex]

We conclude that [latex](4,-2)[/latex] is the solution to the system.

Answer

The solution is [latex](4,-2)[/latex].

Next try one on your own using the same software you will use in our homework sets:

Example 10

Solve the system of equations graphically.

[latex]\begin{array}{r}-x+2y=4\\ 2x-4y=-8\end{array}[/latex]

Show Solution

First we graph the lines, once again using any method. Since both equations are in standard form, we could quickly determine the intercepts. Interestingly, substituting in [latex]y=0[/latex] gives an x-intercept of [latex](-4,0)[/latex] in both equations. Similarly, substituting [latex]x=0[/latex] implies that both equations have a y-intercept of [latex](0,2)[/latex]. It follows that the equations represent the same line, as shown in the graph.

In this case, we know there are an infinite number of solutions. This is written as seen below.

Answer

The solution set is [latex]\left\{(x,y)\hspace{.01in} | \hspace{.01in} -x+2y=4\right\}[/latex].

Exploring the Notation

While there are an infinite number of solutions, not every point in the coordinate plane is a solution; only points that lie on the lines are solutions. We can express this using set-builder notation.

[latex]\{(x,y)\hspace{.01in}|\hspace{.01in}-x+2y=4\}[/latex]

It does not matter which of the two equations we use inside the set-builder notation since we determined they represent the same line anyway.  This notation indicates that the solution is the set of all points [latex](x,y)[/latex] such that the points satisfy the given equation.

While it is both important and helpful to be able to visualize the solution to a system, there is a distinct drawback with graphing. While our solutions all turned out to be relatively nice, this may not always be the case. What if the solution contains coordinates that are extremely large values? Or what if the point of intersection contains decimals or fractions? It could be difficult to impossible to determine the solution by simply looking at a graph in such cases.

In the next two sections, we will address this issue by learning some algebraic methods for finding solutions to systems of equations.