Solve a system of equations using the substitution method

In the previous section, we verified that ordered pairs were potential solutions to systems, and we used graphs to classify how many solutions a system of two linear equations had. What if we are not given a point of intersection, or it is not obvious from a graph? Can we still find a solution to the system? Of course you can, using algebra!

In this section we will learn the substitution method for finding a solution to a system of linear equations in two variables. We have used substitution in different ways throughout this course.  For example, when we were using formulas, we substituted values that we knew into the formula to solve for values that we did not know.  The idea is similar when applied to solving systems, there are just a few different steps in the process. You will first solve for one variable, and then substitute that expression into the other equation. Let’s start with an example to see what this means.

You can substitute a value for a variable even if it is an expression. Here’s an example.

Remember, a solution to a system of equations must be a solution to each of the equations within the system. The ordered pair [latex](4,−1)[/latex] does work for both equations, so you know that it is a solution to the system.

Let’s look at another example whose substitution involves the distributive property.

In the examples above, one of the equations was already given to us in terms of the variable x or y. This allowed us to quickly substitute into the other equation and solve for one of the unknowns.

Sometimes you may have to rewrite one of the equations in terms of one of the variables first before you can substitute. In the example below, you will first need to isolate one of the variables before you can substitute it into the other equation.

In the following video, you will be given an example of solving a systems of two equations using the substitution method.

If you had chosen the other equation to start with in the previous example, you would still be able to find the same solution.  It is really a matter of preference because sometimes solving for a variable will result in having to work with fractions.  As you become more experienced with algebra, you will be able to anticipate what choices will lead to more desirable outcomes.

Recognize systems of equations that have no solution or an infinite number of solutions

When we learned methods for solving linear equations in one variable, we found that some equations didn’t have any solutions, and others had an infinite number of solutions.  We saw this behavior again when we started describing solutions to systems of equations in two variables.

Recall this example from Module 1 for solving linear equations in one variable:

Solve for x. [latex]12+2x–8=7x+5–5x[/latex]

[latex]\displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\end{array}[/latex]

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\,\,\,\,\,\,\,\underline{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\,\,\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4= \,5\end{array}[/latex]

This false statement implies there are no solutions to this equation.  In the same way, you may see an outcome like this when you use the substitution method to find a solution to a system of linear equations in two variables. In the next example, you will see an example of a system of two equations that does not have a solution.

You get the false statement [latex]−8=4[/latex]. What does this mean? The graph of this system sheds some light on what is happening.

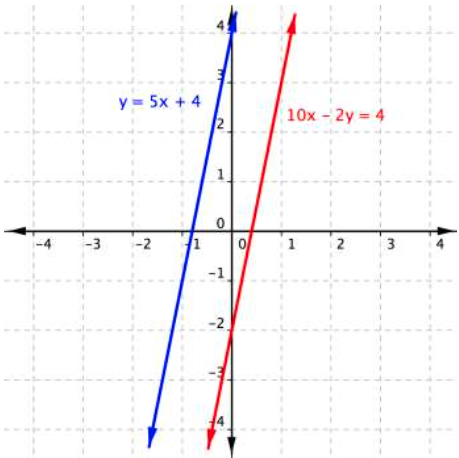
The lines are parallel, they never intersect and there is no solution to this system of linear equations. Note that the result [latex]−8=4[/latex] is not a solution. It is simply a false statement and it indicates that there is no solution.

We have also seen linear equations in one variable and systems of equations in two variables that have an infinite number of solutions.  In the next example, you will see what happens when you apply the substitution method to a system with an infinite number of solutions.

This time you get a true statement: [latex]2=2[/latex]. But what does this type of answer mean? Again, graphing can help you make sense of this system.

This system consists of two equations that both represent the same line. Every point along the line will be a solution to the system, and that’s why the substitution method yields a true statement. In this case, there are an infinite number of solutions.

In the previous section, we learned that we can write the solution set in this case as the following:

[latex]\{(x,y)\hspace{.01in}|\hspace{.01in}y=-\frac{1}{2}x+\frac{1}{3}\}[/latex]

In the following video you will see an example of solving a system that has an infinite number of solutions.

In the next video you will see an example of solving a system of equations that has no solutions.

Summary

The substitution method is one way of solving systems of equations. To use the substitution method, use one equation to find an expression for one of the variables in terms of the other variable. Then substitute that expression in place of that variable in the second equation. You can then solve this equation as it will now have only one variable. Solving using the substitution method will yield one of three results: a single value for each variable within the system (indicating one solution), an untrue statement (indicating no solutions), or a true statement (indicating an infinite number of solutions).