section 6.8 Learning Objectives
6.8: Further Exploration with Quadratic Equations
- Solve application problems (area problems using factoring)
- Solve application problems (consecutive integer problems using factoring)
- Graph basic quadratic functions
Applications of Solving Factorable Quadratic Equations
When a polynomial is set equal to a value (whether an integer or another polynomial), the result is an equation. An equation that can be written in the form [latex]ax^{2}+bx+c=0[/latex] is called a quadratic equation. You can solve some quadratic equations using the rules of algebra, applying factoring techniques, and by using the Principle of Zero Products.
There are many applications for quadratic equations. Don’t forget that to use the Principle of Zero Products to solve a quadratic equation, you need to make sure that the equation is equal to zero. For example, [latex]12^{2}+11x+2=7[/latex] must first be changed to [latex]12x^{2}+11x-5=0[/latex] by subtracting 7 from both sides.
Area Problems
In our first example, we use some basic geometry as we search for the dimensions of rectangle.
Example 1
The area of a rectangular garden is 30 square feet. If the length is 7 feet longer than the width, find the dimensions.
In the example in the following video, we present another area application of factoring trinomials.
Consecutive Integers
Our next example is deceptively similar to the rectangular garden (see if you can recognize this). First, we must recall what is meant by “consecutive integers.” Two consecutive integers would be something like 7 and 8 or -53 and -52. We can also explore consecutive odd integers (such as 15 and 17) or consecutive even integers (like 84 and 86).
ExAMPLE 2
The product of two consecutive odd integers is 63. Find all such pairs of integers.
Graphing Basic Quadratic Functions
In Modules 5 and 6 we learned about polynomials. An equation containing a second-degree polynomial is called a quadratic equation. For example, equations such as [latex]{x}^{2}-3x-4=0[/latex] and [latex]{x}^{2}-16=0[/latex] are in the “family” of quadratic equations. They are used in countless ways in the fields of engineering, architecture, finance, biological science, and, of course, mathematics.
Just like the linear functions we’ve learned about previously, quadratic functions can also be graphed. It is helpful to have an idea about what the shape should be so you can be sure that you have chosen enough points to plot as a guide. Let us start with the most basic quadratic function, [latex]f(x)=x^{2}[/latex].
Graph [latex]f(x)=x^{2}[/latex].
We’ll start with a table of values. Then think of each row of the table as an ordered pair.
| [latex]x[/latex] | [latex]f(x)=x^2[/latex] |
| [latex]−2[/latex] | [latex](-2)^2=4[/latex] |
| [latex]−1[/latex] | [latex](-1)^2=1[/latex] |
| [latex]0[/latex] | [latex](0)^2=0[/latex] |
| [latex]1[/latex] | [latex](1)^2=1[/latex] |
| [latex]2[/latex] | [latex](2)^2=4[/latex] |
Now we’ll plot the points [latex](-2,4), (-1,1), (0,0), (1,1), (2,4)[/latex]
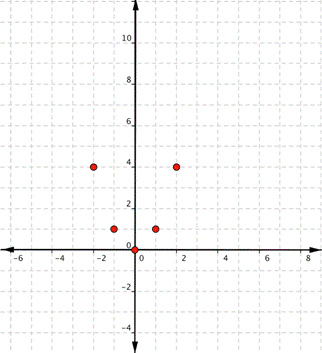
Notice that the quadratic family of functions is not drawn using straight lines. Since the points are not on a line, you cannot use a straight edge. Connect the points as best you can using a smooth curve (not a series of straight lines). You may want to find and plot additional points (such as the ones in blue below). Placing arrows on the tips of the lines implies that they continue in that direction forever.
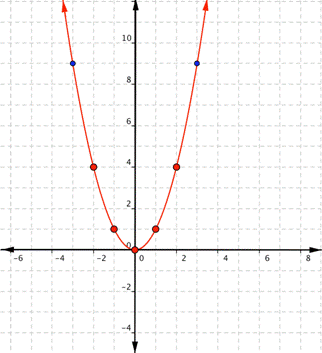
Notice that the shape is similar to the letter U. This is called a parabola. One-half of the parabola is a mirror image of the other half. The lowest point on this graph is called the vertex. The vertical line that goes through the vertex is called the line of symmetry. In this case, that line is the y-axis, which is the line [latex]x=0[/latex].
In the following video, we show an example of graphing another quadratic function, [latex]f(x)=\frac{1}{2}x^2[/latex], using a table of values.
The equations for quadratic functions can be written in the form [latex]f(x)=ax^{2}+bx+c[/latex] (where [latex]a\ne 0[/latex]). In the two basic quadratic functions we graphed above, notice there was only the [latex]ax^2[/latex] term and that both [latex]b=0[/latex], and [latex]c=0[/latex] for those functions.
Although there are many forms that quadratic functions can be written in, this Elementary Algebra course will focus primarily on graphing basic quadratic functions of the form [latex]f(x)=ax^{2}+c[/latex].
Quadratic functions of the form [latex]f(x)=ax^{2}+c[/latex] will always be centered around the y-axis which is the line [latex]x=0[/latex].
We have shared two examples above of graphing a basic quadratic function of the form [latex]f(x)=ax^{2}+c[/latex], where [latex]c=0[/latex], so let’s now explore how to graph a quadratic function of the form [latex]f(x)=ax^{2}+c[/latex] where [latex]c\ne 0[/latex] .
Graph [latex]f(x)=x^{2}-4[/latex].
Similar to the problems above, lets start with a table of values.
| [latex]x[/latex] | [latex]f(x)=x^2-4[/latex] | [latex]f(x)[/latex] |
| [latex]−2[/latex] | [latex](-2)^2-4 = 4-4 = 0[/latex] | 0 |
| [latex]−1[/latex] | [latex](-1)^2-4 = 1-4 = -3[/latex] | -3 |
| [latex]0[/latex] | [latex](0)^2-4 = 0-4 = -4[/latex] | -4 |
| [latex]1[/latex] | [latex](1)^2-4 = 1-4 = -3[/latex] | -3 |
| [latex]2[/latex] | [latex](2)^2-4 = 4-4 = 0[/latex] | 0 |
We’ll now plot the points [latex](-2,0), (-1,-3), (0,-4), (1,-3), (2,0)[/latex] on the graph.

If we connect all the points with a smooth curve we will have the graph of our function [latex]f(x)=x^{2}-4[/latex].

Let’s have you now try one on your own:
Example 3
Graph the function: [latex]f(x)=x^2-16[/latex]
Lets try a few more examples.
Example 4
Graph the function: [latex]f(x)=x^2+5[/latex]
In the next example we will explore how parabolas don’t always open upwards.
Example 5
Graph the function: [latex]f(x)=-3x^2[/latex]
As we saw with the last example, with quadratic functions of the form [latex]f(x)=ax^{2}+c[/latex], changing the value of [latex]a[/latex] can change the width of the parabola and whether it opens up ([latex]a>0[/latex]) or down ([latex]a<0[/latex]). If [latex]a[/latex] is positive, the vertex is the lowest point, and the parabola opens up. If [latex]a[/latex] is negative, the vertex is the highest point, and the parabola opens down. Whereas Examples 3 and 4 showed that the value of [latex]c[/latex] moves the parabola up or down.
When graphing quadratic functions of the form [latex]f(x)=ax^{2}+c[/latex] follow the steps below:
- Recognize the form of the quadratic function and that it will be a parabola centered around x=0.
- Make a table of values, making sure to choose some values on either side of x=0, as well as the value of x=0.
- Plot your points and connect them with a smooth curve into a parabola shape.
The next example reveals what can cause a parabola to move right or left.
Example 6
Graph the function: [latex]f(x)=(x-4)^2[/latex]
The key to the last example is we no longer focused on choosing values around [latex]x=0[/latex]. Instead, we considered what would cause the quantity inside the parentheses to equal to zero, which was [latex]x=4[/latex], plugging in this number and values on either side of it. If the function had been [latex]f(x)=(x+4)^2[/latex], the primary [latex]x[/latex]-value of interest would have been [latex]x=-4[/latex]. We can describe this using the form given below.
When graphing quadratic functions of the form [latex]f(x)=a(x-h)^{2}[/latex] follow the steps below:
- Recognize the form of the quadratic function and that it will be a parabola centered around x=h.
- Make a table of values, making sure to choose some values on either side of x=h, as well as the value of x=h.
- Plot your points and connect them with a smooth curve into a parabola shape.
Not all parabolas fall into the two forms given here. While you will explore these in more detail in future math classes, we end with a preview, including an application of the factoring skills we have learned.
Think About it
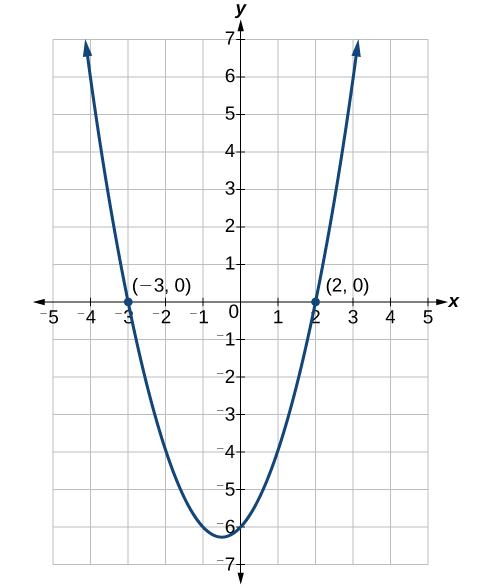
Graph the equation: [latex]f(x)={x}^{2}+x - 6[/latex]. (It may be helpful to factor it, and set it equal to 0 to find the [latex]x[/latex]-intercepts.)
Graphing Quadratics Summary
Creating a graph of a function is one way to understand the relationship between the inputs and outputs of that function. Creating a graph can be done by choosing values for x, finding the corresponding y values, and plotting them. However, it helps to understand the basic shape of the function. Knowing how changes to the basic function equation affect the graph is also helpful.
The shape of a quadratic function is a parabola. Parabolas have the equation [latex]f(x)=ax^{2}+bx+c[/latex], where [latex]a, b[/latex] and [latex]c[/latex] are real numbers and [latex]a\ne0[/latex]. The value of [latex]a[/latex] determines the width and the direction of the parabola, while the vertex depends on the values of [latex]a, b[/latex] and [latex]c[/latex].