
Bits and Bytes
Exponents allow us to perform repeated multiplication quickly and to write very large or small numbers in a way that is easy to understand. There are many and varied uses of exponents that you may be surprised to find are all around us. Have you ever heard a computer described as having a 32-bit processor with 64 megabytes of RAM and 2.1 gigabytes of hard disk space? What on earth does that even mean? This terminology is used to describe how fast a computer can process information, which results in how quickly it responds after you click on an app or open a file. It also describes how much memory the computer has to store the files and apps you want to use with it.
Computers use binary digits (0 and 1) instead of the decimal digits (0 to 9) we are used to working with. The descriptions 32-bit and 64 megabytes don’t make much sense at first glance, but you can use the lingua franca of exponents to translate this information into an explanation of how memory and processing speed work.
Each binary digit is equivalent to one bit, and a byte contains 8 bits, often called a binary octet. Each character that you type on a computer needs one binary octet in order to exist. This is what a byte represents relative to decimal numbers:
| Type of Number | Decimal Equivalent | ||||||||
| Decimal Powers of 2 | [latex]2^7[/latex] | [latex]2^6[/latex] | [latex]2^5[/latex] | [latex]2^4[/latex] | [latex]2^3[/latex] | [latex]2^2[/latex] | [latex]2^1[/latex] | [latex]2^0[/latex] | |
| Decimal Number | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | [latex]128+64+32+16+8+4+2+1=255[/latex] |
| Binary Octet | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | [latex]2+1=3[/latex] | |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | [latex]8+4+2=14[/latex] | |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | [latex]128+32+8+4=172[/latex] |
The 1s in the binary octet act as light switches within a computer. The computer uses the binary octets to represent characters such as numbers, letters, and other information. You can think of the number of bits assigned to a computer processor as the amount of “scratch pad” it has available to store calculations and information while it works. Having more “scratch pad” available means the computer can do more without needing to access memory which takes time. There are many more factors that influence the speed and agility of a computer, but the basics can be described with exponents. Now try to imagine how many bytes the Millennium Falcon’s computer must have needed to make the Kessel Run in less than 12 parsecs!
Why learn about polynomials?
If you have ever watched a Pixar movie, you have seen computer generated images. A very common method for generating graphics with a computer is to use what is called a wire mesh. You can think of a wire mesh as a grid – like the ones we have used to graph lines – that has been bent and stretched to make a shape we want, as in the image of a dolphin below.

The dolphin in the image was created by plotting points in space to create connected triangles. This method of rendering graphics works well and is in wide use, but it takes a lot of computer memory. Recently, researchers have been investigating the use of polynomials for rendering graphics in part because it demands less memory in the process.[1]. In this process, the surfaces that are rendered are made from solutions to algebraic polynomials. The image below shows some images of smooth-surfaced objects that were rendered using polynomials by researchers Charles Loop and Jim Blinn from Microsoft.
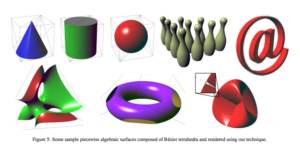
Surfaces Rendered Using Polynomials.
In this module, we learn about how to identify a polynomial and how to perform algebraic operations on polynomials (which also involved using rules of exponents). Like the linear equations and inequalities you learned about earlier, polynomials are useful in many applications of mathematics as well as in other disciplines like biology, economics, and even cryptology. Gaining a basic understanding of their qualities and how the rules of algebra we have learned so far apply to them will help you learn how to use polynomials both inside and out of your math class.
- Loop, Charles, and Jim Blinn. Real-time GPU Rendering of Piecewise Algebraic Surfaces. ACM SIGGRAPH 2006 Papers on - SIGGRAPH '06 (2006): n. pag. Web. ↵