Learning Outcomes
- Add and subtract real numbers
- Add real numbers with the same and different signs
- Subtract real numbers with the same and different signs
- Simplify combinations that require both addition and subtraction of real numbers.
- Multiply and divide real numbers
- Multiply two or more real numbers.
- Divide real numbers
- Simplify expressions with both multiplication and division
- Simplify compound expressions with real numbers
- Use the Order of Operations to simplify an expression
- Simplify expressions containing exponents
- Simplify expressions with multiple grouping symbols
- Simplify expressions containing absolute values
Some important terminology to remember before we begin is as follows:
- integers: counting numbers like 1, 2, 3, etc., including negatives and zero
- real number: fractions, negative numbers, decimals, integers, and zero are all real numbers
- absolute value: a number’s distance from zero; it’s always positive. [latex]|-7| = 7[/latex]
- sign: this refers to whether a number is positive or negative, we use [latex]+[/latex] for positive (to the right of zero on the number line) and [latex]-[/latex] for negative (to the left of zero on the number line)
- difference: the result of subtraction
- sum: the result of addition
The ability to work comfortably with negative numbers is essential to success in algebra. For this reason we will do a quick review of adding, subtracting, multiplying and dividing integers. Integers are all the positive whole numbers, zero, and their opposites (negatives). As this is intended to be a review of integers, the descriptions and examples will not be as detailed as a normal lesson.
Add and subtract real numbers
Add real numbers
In this section, we will use the skills from the last section to simplify mathematical expressions that contain many grouping symbols and many operations. We are using the term compound to describe expressions that have many operations and many grouping symbols. More care is needed with these expressions when you apply the order of operations. Additionally, you will see how to handle absolute value terms when you simplify expressions.
When adding integers we have two cases to consider. The first case is whether the signs match (both positive or both negative). If the signs match, we will add the numbers together and keep the sign.
Example 1
- Add 21 + 34
- Add -18 + (-13)
If the signs don’t match (one positive and one negative number) we will subtract the numbers (as if they were all positive) and then use the sign from the larger number. This means if the larger number is positive, the answer is positive. If the larger number is negative, the answer is negative.
Example 2
- Add [latex]-10+6[/latex]
- Add [latex]12+(- 4)[/latex]
To add two numbers with the same sign (both positive or both negative)
- Add their absolute values (without the [latex]+[/latex] or [latex]-[/latex] sign)
- Give the sum the same sign.
To add two numbers with different signs (one positive and one negative)
- Find the difference oftheir absolute values. (Note that when you find the difference of the absolute values, you always subtract the lesser absolute value from the greater one.)
- Give the sum the same sign as the number with the greater absolute value.
Subtract real numbers
Subtraction can be defined as “adding the opposite.” In the following example, we will rewrite the subtraction problem as adding the opposite and apply what we learned about adding real numbers to simplify.
Example 3
Find [latex]23–73[/latex].
Another way to think about subtracting is to think about the distance between the two numbers on the number line. In the example below, [latex]382[/latex] is to the right of 0 by [latex]382[/latex] units, and [latex]−93[/latex] is to the left of 0 by 93 units. The distance between them is the sum of their distances to 0: [latex]382+93[/latex].

Example 4
Find [latex]382–\left(−93\right)[/latex].
The following video explains how to subtract two signed integers.
Example 5
Find [latex]-\frac{3}{7}-\frac{6}{7}+\frac{2}{7}[/latex]
In the following video you will see an example of how to add three fractions with a common denominator that have different signs.
Example 6
Evaluate [latex]27.832+(−3.06)[/latex]. When you add decimals, remember to line up the decimal points so you are adding tenths to tenths, hundredths to hundredths, and so on.
In the following video are examples of adding and subtracting decimals with different signs.
Multiply and divide real numbers
Multiplication and division are inverse operations, just as addition and subtraction are. You may recall that when you divide fractions, you multiply by the reciprocal. Inverse operations “undo” each other.
Multiply real numbers
Multiplying real numbers is not that different from multiplying whole numbers and positive fractions. However, you haven’t learned what effect a negative sign has on the product.
With whole numbers, you can think of multiplication as repeated addition. Using the number line, you can make multiple jumps of a given size. For example, the following picture shows the product [latex]3\cdot4[/latex] as 3 jumps of 4 units each.
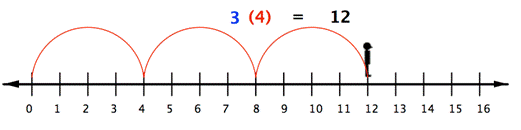
So to multiply [latex]3(−4)[/latex], you can face left (toward the negative side) and make three “jumps” forward (in a negative direction).
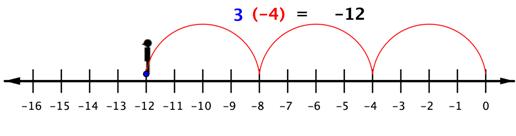
The product of a positive number and a negative number (or a negative and a positive) is negative.
The Product of a Positive Number and a Negative Number
To multiply a positive number and a negative number, multiply their absolute values. The product is negative.
Example 7
Find [latex]−3.8(0.6)[/latex].
The following video contains examples of how to multiply decimal numbers with different signs.
The Product of Two Numbers with the Same Sign (both positive or both negative)
To multiply two positive numbers, multiply their absolute values. The product is positive.
To multiply two negative numbers, multiply their absolute values. The product is positive.
Example 8
Find [latex]~\left( -\frac{3}{4} \right)\left( -\frac{2}{5} \right)[/latex]
The following video shows examples of multiplying two signed fractions, including simplification of the answer.
To summarize:
- positive [latex]\cdot[/latex] positive: The product is positive.
- negative [latex]\cdot[/latex] negative: The product is positive.
- negative [latex]\cdot[/latex] positive: The product is negative.
- positive [latex]\cdot[/latex] negative: The product is negative.
You can see that the product of two negative numbers is a positive number. So, if you are multiplying more than two numbers, you can count the number of negative factors.
Multiplying More Than Two Negative Numbers
If there are an even number (0, 2, 4, …) of negative factors to multiply, the product is positive.
If there are an odd number (1, 3, 5, …) of negative factors, the product is negative.
Example 9
Find [latex]3(−6)(2)(−3)(−1)[/latex].
The following video contains examples of multiplying more than two signed integers.
Divide real numbers
You may remember that when you divided fractions, you multiplied by the reciprocal. Reciprocal is another name for the multiplicative inverse (just as opposite is another name for additive inverse).
An easy way to find the multiplicative inverse is to just “flip” the numerator and denominator as you did to find the reciprocal. Here are some examples:
- The reciprocal of [latex]\frac{4}{9}[/latex] is [latex]\frac{9}{4}[/latex]because [latex]\frac{4}{9}\left(\frac{9}{4}\right)=\frac{36}{36}=1[/latex].
- The reciprocal of 3 is [latex]\frac{1}{3}[/latex] because [latex]\frac{3}{1}\left(\frac{1}{3}\right)=\frac{3}{3}=1[/latex].
- The reciprocal of [latex]-\frac{5}{6}[/latex] is [latex]\frac{-6}{5}[/latex] because [latex]-\frac{5}{6}\left( -\frac{6}{5} \right)=\frac{30}{30}=1[/latex].
- The reciprocal of 1 is 1 as [latex]1(1)=1[/latex].
When you divided by positive fractions, you learned to multiply by the reciprocal. You also do this to divide real numbers.
Think about dividing a bag of 26 marbles into two smaller bags with the same number of marbles in each. You can also say each smaller bag has one half of the marbles.
[latex]26\div 2=26\left( \frac{1}{2} \right)=13[/latex]
Notice that 2 and [latex]\frac{1}{2}[/latex] are reciprocals.
Try again, dividing a bag of 36 marbles into smaller bags.
| Number of bags | Dividing by number of bags | Multiplying by reciprocal |
|---|---|---|
| 3 | [latex]\frac{36}{3}=12[/latex] | [latex]36\left( \frac{1}{3} \right)=\frac{36}{3}=\frac{12(3)}{3}=12[/latex] |
| 4 | [latex]\frac{36}{4}=9[/latex] | [latex]36\left(\frac{1}{4}\right)=\frac{36}{4}=\frac{9\left(4\right)}{4}=9[/latex] |
| 6 | [latex]\frac{36}{6}=6[/latex] | [latex]36\left(\frac{1}{6}\right)=\frac{36}{6}=\frac{6\left(6\right)}{6}=6[/latex] |
Dividing by a number is the same as multiplying by its reciprocal. (That is, you use the reciprocal of the divisor, the second number in the division problem.)
Example 10
Find [latex]28\div \frac{4}{3}[/latex]
Now let’s see what this means when one or more of the numbers is negative. A number and its reciprocal have the same sign. Since division is rewritten as multiplication using the reciprocal of the divisor, and taking the reciprocal doesn’t change any of the signs, division follows the same rules as multiplication.
Rules of Division
When dividing, rewrite the problem as multiplication using the reciprocal of the divisor as the second factor.
When one number is positive and the other is negative, the quotient is negative.
When both numbers are negative, the quotient is positive.
When both numbers are positive, the quotient is positive.
Example 11
Find [latex]24\div\left(-\frac{5}{6}\right)[/latex].
Example 12
Find [latex]4\,\left( -\frac{2}{3} \right)\,\div \left( -6 \right)[/latex]
The following video explains how to divide signed fractions.

Remember that a fraction bar also indicates division, so a negative sign in front of a fraction goes with the numerator, the denominator, or the whole fraction: [latex]-\frac{3}{4}=\frac{-3}{4}=\frac{3}{-4}[/latex].
In each case, the overall fraction is negative because there’s only one negative in the division.
The following video explains how to divide signed fractions.
Simplify compound expressions with real numbers
In this section, we will simplify mathematical expressions that contain many grouping symbols and many operations. We are using the term compound to describe expressions that have many operations and sometimes many grouping symbols. Additionally, you will see how to handle absolute value terms when you simplify expressions.
Use the order of operations to simplify an expression
You may or may not recall the order of operations for applying several mathematical operations to one expression. Just as it is a social convention for us to drive on the right-hand side of the road, the order of operations is a set of conventions used to provide order when you are required to use several mathematical operations for one expression. The graphic below depicts the order in which mathematical operations are performed.
![steps of order of operations that say Perform all operations within grouping symbols first. Grouping symbols include {}, [], () Evaluate exponents or square roots Multiply or divide from left to right Add or subtract from left to right](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/117/2016/06/17181059/Screen-Shot-2016-06-17-at-10.57.52-AM-300x183.png)
Order of operations
Example 13
Simplify [latex]7–5+3\cdot8[/latex].
In the following example, you will be shown how to simplify an expression that contains both multiplication and subtraction using the order of operations.
When you are applying the order of operations to expressions that contain fractions, decimals, and negative numbers, you will need to recall how to do these computations as well.
Example 14
Simplify [latex]3\cdot\frac{1}{3}-8\div\frac{1}{4}[/latex].
In the following video you are shown how to use the order of operations to simplify an expression that contains multiplication, division, and subtraction with terms that contain fractions.
Simplify expressions containing exponents
When you are evaluating expressions, you will sometimes see exponents used to represent repeated multiplication. Recall that an expression such as [latex]7^{2}[/latex] is exponential notation for [latex]7\cdot7[/latex]. (Exponential notation has two parts: the base and the exponent or the power. In [latex]7^{2}[/latex], 7 is the base and 2 is the exponent; the exponent determines how many times the base is multiplied by itself.)
Exponents are a way to represent repeated multiplication; the order of operations places it before any other multiplication, division, subtraction, and addition is performed.
Example 15
Simplify [latex]3^{2}\cdot2^{3}[/latex].
In the video that follows, an expression with exponents on its terms is simplified using the order of operations.
Simplify expressions containing multiple grouping symbols
Grouping symbols such as parentheses ( ), brackets [ ], braces[latex]\displaystyle \left\{ {} \right\}[/latex], and fraction bars can be used to further control the order of the four arithmetic operations. The rules of the order of operations require computation within grouping symbols to be completed first, even if you are adding or subtracting within the grouping symbols and you have multiplication outside the grouping symbols. After computing within the grouping symbols, divide or multiply from left to right and then subtract or add from left to right. When there are grouping symbols within grouping symbols, calculate from the inside to the outside. That is, begin simplifying within the innermost grouping symbols first.
Remember that parentheses can also be used to show multiplication. In the example that follows, both uses of parentheses—as a way to represent a group, as well as a way to express multiplication—are shown.
Example 16
Simplify [latex]\left(3+4\right)^{2}+\left(8\right)\left(4\right)[/latex].
Example 17
Simplify [latex]4\cdot{\frac{3[5+{(2 + 3)}^2]}{2}}[/latex]
In the following video, you are shown how to use the order of operations to simplify an expression with grouping symbols, exponents, multiplication, and addition.
Think About It
These problems are very similar to the examples given above. How are they different and what tools do you need to simplify them?
a) Simplify [latex]\left(1.5+3.5\right)–2\left(0.5\cdot6\right)^{2}[/latex]. This problem has parentheses, exponents, multiplication, subtraction, and addition in it, as well as decimals instead of integers.
Use the box below to write down a few thoughts about how you would simplify this expression with decimals and grouping symbols.
b) Simplify [latex]{{\left( \frac{1}{2} \right)}^{2}}+{{\left( \frac{1}{4} \right)}^{3}}\cdot \,32[/latex].
Use the box below to write down a few thoughts about how you would simplify this expression with fractions and grouping symbols.
Example 18
Simplify [latex]\frac{5-[3+(2\cdot (-6))]}{{{3}^{2}}+2}[/latex]
The video that follows contains an example similar to the written one above. Note how the numerator and denominator of the fraction are simplified separately.
Simplify expressions containing absolute values
Absolute value expressions are one final method of grouping that you may see. Recall that the absolute value of a quantity is always positive or 0.
When you see an absolute value expression included within a larger expression, treat the absolute value like a grouping symbol and evaluate the expression within the absolute value sign first. Then take the absolute value of that expression. The example below shows how this is done.
Example 19
Simplify [latex]\frac{3+\left|2-6\right|}{2\left|3\cdot1.5\right|-\left(-3\right)}[/latex].
The following video uses the order of operations to simplify an expression in fraction form that contains absolute value terms. Note how the absolute values are treated like parentheses and brackets when using the order of operations.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot Combo Meal. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex 2: Subtracting Integers (Two Digit Integers). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/ciuIKFCtWWU. License: CC BY: Attribution
- Find the Sum and Difference of Three Signed Fractions (Common Denom). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/P972VVbR98k. License: CC BY: Attribution
- Ex: Adding Signed Decimals. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/3FHZQ5iKcpI. License: CC BY: Attribution
- Unit 9: Real Numbers, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
- Ex: Multiplying Three or More Integers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/rx8F9SPd0HE. License: CC BY: Attribution
- Ex: Multiplying Signed Fractions . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/yUdJ46pTblo. License: CC BY: Attribution
- Ex 1: Dividing Signed Fractions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/OPHdadhDJoI. License: CC BY: Attribution
- Ex 2: Combining Like Terms. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/b9-7eu29pNM. License: CC BY: Attribution
- Simplify an Expression in the Form: a-b+c*d. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/yFO_0dlfy-w. License: CC BY: Attribution
- Simplify an Expression in the Form: a*1/b-c/(1/d). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/yqp06obmcVc. License: CC BY: Attribution
- Simplify an Expression in the Form: (a+b)^2+c*d. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/EMch2MKCVdA. License: CC BY: Attribution
- Simplify an Expression in Fraction Form. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/xIJLq54jM44. License: CC BY: Attribution
- Simplify an Expression in Fraction Form with Absolute Values. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/6wmCQprxlnU. License: CC BY: Attribution