Learning Outcomes
- Determine whether an ordered triple is a solution of a system of three linear equations with three variables.
- Solve systems of three linear equations with three variables.
- Determine if a system of three linear equations with three variables is inconsistent or consistent.
- Determine if equations are dependent or independent for a system of three linear equations with three variables.
Sometimes in problems or applications there are three (or more) unknowns. A system with three unknowns requires three equations in order to generally have a single solution (although just like with two variables, there are special cases.) We typically use [latex]z[/latex] for the third variable. An example of a system with three variables is shown here:
[latex]\begin{array}{l}\phantom{6}x+\phantom{4}y+\phantom{5}z=2\hfill \\ 6x - 4y+5z=31\hfill \\ 5x+2y+2z=13\hfill \end{array}[/latex]
A solution to a system of three equations in three variables is an ordered triple [latex]\left(x,y,z\right)[/latex] that makes all three equations true. Graphically, the solution set to a single linear equation in three variables can be represented by a plane in three dimensions. A plane is a flat two-dimensional surface that extends infinitely. A system of three equations represents three planes, and a solution represents a common intersection point.
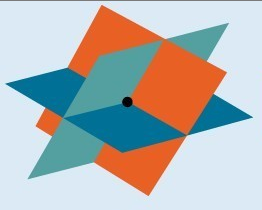
You can visualize such an intersection by imagining any corner in a rectangular room. A line is defined by the the intersection of two planes: for example, two adjacent walls. A corner is defined by the intersection of three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.
In the first example, we will determine whether an ordered triple is a solution for a system of three linear equations in three variables.
Example
Determine whether the ordered triple [latex]\left(3,-2,1\right)[/latex] is a solution to the system.
Solving a Three-Variable System
As with many math processes, our goal is to reduce our problem to a problem that was previously solved. If we can eliminate one of the variables, that will result in a system with only two variables and we know how to solve those.
Consider the following example, which begins with [latex]x[/latex] already removed from two of the equations.
Example
Solve the system of equations.
The strategy we used in the preceding example informs the general process that we will use to solve systems with three unknowns.
Solving a linear system with three unknowns
- Pick any pair of equations and eliminate one variable.
- Pick another pair of equations and eliminate the same variable.
- You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
Since our previous example started already in Step 3, we will now do an example where we must do all four of the steps.
EXAMPLE
Solve the system of equations.
[latex]\left\{\begin{array}{lr}2x+\phantom{4}y+4z=3&(1)\\ -x + 3y-4z=6&(2)\\ 3x-5y+4z=2&(3) \end{array}\right.[/latex]
Some students prefer to always eliminate [latex]x[/latex] first so that the approach to each problem is consistent. While this can be a good strategy, it also can cause some of the steps to take more time as we must first multiply some equations by a constant to set up the [latex]x[/latex] to eliminate.
In the following videos, we show more examples of the algebra you may encounter when solving systems with three variables.
Inconsistent and Dependent
The systems we have seen so far in this section were consistent and independent. A system is consistent if it has at least one solution. Just as with systems of equations in two variables, we may come across an inconsistent system of equations in three variables, which means that it does not have a solution that satisfies all three equations. The process of elimination will result in a false statement, such as [latex]0=5[/latex] or some other contradiction. There is also a notion of dependent system, and it is identified in the same way as with two variables – the elimination process results in a true statement, such as [latex]0=0[/latex]. This happens when one or more of the equations is “redundant” and does not affect the solution set at all. Here is a visual representation of these cases.
Infinitely Many or No Solutions
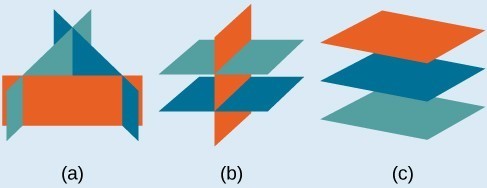
- Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex]. Graphically, a system with no solution is represented by three planes with no point in common. This illustration shows a few ways that three planes can have no common intersection point. Note that a solution must be a single point at which all three planes intersect.
- Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space. The graphic below shows how three planes can intersect to form a line giving the system infinitely many solutions. This system is dependent because if one of the planes was removed, the solution set would still be the same line.
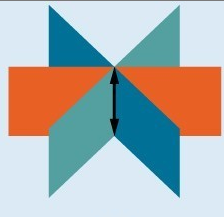
Infinitely many solutions.
In the following example, we will see how it is possible to have a system with three variables and no solutions.
Example
Solve the system of equations.
[latex]\left\{\begin{array}{rll}x - 3y+\phantom{4}z&=\:4&(1)\\ -\phantom{3}y-4z&=\:7 &(2)\\ \phantom{11}2y+8z&=\:-12&(3)\end{array}\right.[/latex]
We will show another example of using elimination to solve a system in three variables that ends up having no solution in the following video.
The next example shows a dependent system with three variables. In this book we will not describe the solution of dependent systems with three variables other than just to say “infinite solutions.” A more complete description is possible, but saved for later math courses.
Example
Solve the system of equations.
[latex]\left\{\begin{array}{lr}\phantom{-10x}-4y+4z=-5&(1)\\ -10x + 2y-6z=-6&(2)\\ -\phantom{5}5x-3y+\phantom{4}z=-8&(3) \end{array}\right.[/latex]
In our last video example, we show a system that has an infinite number of solutions. You do not need to watch the part of the video where the infinite solutions are described in more detail using the variable [latex]t,[/latex] but you can if you are curious.
Summary
- A solution to a system of linear equations in three variables is an ordered triple of the form [latex](x,y,z)[/latex].
- Solutions can be verified using substitution. A solution needs to satisfy all three equations.
- Systems of three variables can be solved using the same techniques as we used to solve systems with two variables, including elimination and substitution.
- A system with three variables can have one solution, no solution, or infinitely many solutions.
Candela Citations
- Revision and Adaptation. Located at: http://Lumen%20Learning. License: CC BY: Attribution
- College Algebra: 8.1 Systems of Linear Equations: Gaussian Elimination. Authored by: Stitz, Carl and Zeager, Jeff. Located at: http://www.stitz-zeager.com/szca07042013.pdf. License: CC BY: Attribution
- Ex: Solve a System of 3 Equations with 3 Unknowns Using Back Substitution. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/HHIjTChrIxE. License: CC BY: Attribution
- Ex 2: System of Three Equations with Three Unknowns Using Elimination. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/r6htz3gaHZ0. License: CC BY: Attribution
- Ex 1: System of Three Equations with Three Unknowns Using Elimination. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/3RbVSvvRyeI. License: CC BY: Attribution
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution
