Learning Outcomes
- Simplify expressions by applying the Properties of Exponents
- Multiply polynomials
A common language is needed in order to communicate mathematical ideas clearly and efficiently. Exponential notation was developed to write repeated multiplication more efficiently. For example, growth occurs in living organisms by the division of cells. One type of cell divides [latex]2[/latex] times in an hour. So in [latex]12[/latex] hours, the cell will divide [latex]\overbrace{2\cdot{2}\cdot{2}\cdot{2}\cdot{2}\cdot{2}\cdot{2}\cdot{2}\cdot{2}\cdot{2}\cdot{2}\cdot{2}}^{2^{12}}[/latex] times. This can be expressed more efficiently as [latex]2^{12}[/latex]. In this section we will learn how to simplify and perform mathematical operations such as multiplication and division on terms that have exponents.
Exponential Expressions
We use exponential notation to write repeated multiplication. For example, [latex]10\cdot10\cdot10[/latex] can be written more succinctly as [latex]10^{3}[/latex]. The [latex]10[/latex] in [latex]10^{3}[/latex] is called the base. The [latex]3[/latex] in [latex]10^{3}[/latex] is called the exponent. The expression [latex]10^{3}[/latex] is called the exponential expression. Knowing the names for the parts of an exponential expression will help you learn how to perform mathematical operations on them.
[latex]\text{base}\rightarrow10^{3\leftarrow\text{exponent}}[/latex]
[latex]10^{3}[/latex] is read as “[latex]10[/latex] to the third power” or “[latex]10[/latex] cubed.” It means [latex]10\cdot10\cdot10[/latex], or [latex]1,000[/latex].
[latex]8^{2}[/latex] is read as “[latex]8[/latex] to the second power” or “[latex]8[/latex] squared.” It means [latex]8\cdot8[/latex], or [latex]64[/latex].
[latex]5^{4}[/latex] is read as “[latex]5[/latex] to the fourth power.” It means [latex]5\cdot5\cdot5\cdot5[/latex], or [latex]625[/latex].
[latex]b^{5}[/latex] is read as “[latex]b[/latex] to the fifth power.” It means [latex]{b}\cdot{b}\cdot{b}\cdot{b}\cdot{b}[/latex]. Its value will depend on the value of [latex]b[/latex].
The exponent applies only to the number or the variable that it is attached to. Therefore, in the expression [latex]xy^{4}[/latex], only the [latex]y[/latex] is affected by the [latex]4[/latex]. [latex]xy^{4}[/latex] means [latex]{x}\cdot{y}\cdot{y}\cdot{y}\cdot{y}[/latex]. The [latex]x[/latex] is not being raised to the 4th power.
Consider an expression like [latex]−3^{4}[/latex]. In the previous paragraph, only the [latex]3[/latex] is being raised to the 4th power (not the negative). You can rewrite the expression as [latex]-1\cdot3^{4}[/latex] which means [latex]–1\cdot\left(3\cdot3\cdot3\cdot3\right)[/latex], or [latex]−81[/latex].
If [latex]−3[/latex] is to be the base, it must be written using parentheses as [latex]\left(−3\right)^{4}[/latex], which means [latex](−3)\cdot(−3)\cdot(−3)\cdot(−3)[/latex], or [latex]81[/latex].
Likewise, [latex]\left(−x\right)^{4}=\left(−x\right)\cdot\left(−x\right)\cdot\left(−x\right)\cdot\left(−x\right)=x^{4}[/latex], while [latex]−x^{4}=\ –1\cdot\left(x\cdot x\cdot x\cdot x\right)[/latex].
In the following video, you are provided more examples of applying exponents to various bases.
 Caution! Whether to include a negative sign as part of a base or not often leads to confusion. To clarify whether a negative sign is applied before or after the exponent, here is an example.
Caution! Whether to include a negative sign as part of a base or not often leads to confusion. To clarify whether a negative sign is applied before or after the exponent, here is an example.
What is the difference in the way you would evaluate these two terms?
- [latex]-{3}^{2}[/latex]
- [latex]{\left(-3\right)}^{2}[/latex]
To evaluate 1), you would apply the exponent to the three first, then apply the negative sign last, like this:
[latex]\begin{align}&\quad\,-3^2\\ &=-\left({3}^{2}\right)&\\ &=-\left(9\right) &\\ &= -9\end{align}[/latex]
To evaluate 2), you would apply the exponent to the negative [latex]3[/latex]:
[latex]\begin{align}&\quad\;\left(-3\right)^{2}&\\ &=\left(-3\right)\cdot\left(-3\right)&\\ &={ 9}\end{align}[/latex]
The key to remembering this is to follow the order of operations. The first expression does not include parentheses so you would apply the exponent to the integer [latex]3[/latex] first, then apply the negative sign. The second expression includes parentheses, so hopefully you will remember that the negative sign also gets squared.
Properties of Exponents
Here is an overview of the properties of exponents. For a more detailed explanation and examples of these properties, please click on the property in the table you would like to review to or scroll down to corresponding section below.
If you do not need to review the properties of exponents, you can skip down the page to Polynomial Functions and Expressions where you can review adding, subtracting, and multiplying polynomial expressions and also review evaluating polynomial functions.
| Name | Property | Example |
|---|---|---|
| Product Rule | [latex]{\large a^{m}\cdot{a}^{n}=a^{m+n}}[/latex] | [latex]{\large x^{3}\cdot{x}^{2}=x^{3+2}=x^5}[/latex] |
| Quotient Rule | [latex]{\large \dfrac{a^{m}}{{a}^{n}}=a^{m-n}}[/latex] | [latex]{\large \dfrac{x^{7}}{{x}^{4}}=x^{7-4}=x^3}[/latex] |
| Power Rule | [latex]{\large \left(a^{m}\right)^{n}=a^{m\cdot{n}}}[/latex] | [latex]{\large \left(x^{2}\right)^{4}=x^{2\cdot{4}}=x^8}[/latex] |
| Power of a Product Rule | [latex]{\large \left(ab\right)^{n}=a^{n}\cdot b^{n}}[/latex] | [latex]{\large \left(2y\right)^{3}=2^{3}\cdot y^{3}=8y^3}[/latex] |
| Power of a Quotient Rule | [latex]{\large \left(\dfrac{a}{b}\right)^{n}=\dfrac{{a}^{n}}{{b}^{n}}, b \ne{0}}[/latex] | [latex]{\large \left(\dfrac{x}{3}\right)^{2}=\dfrac{{x}^{2}}{{3}^{2}}=\dfrac{x^2}{9}}[/latex] |
| Zero Exponent Rule | [latex]{\large \left({a}\right)^{0}=1,{a} \ne{0}}[/latex] | [latex]{\large \left({-4x^5}\right)^{0}=1}[/latex] |
| Negative Exponent Rule | [latex]{\large {a}^{-n}=\dfrac{1}{{a}^{n}}, {a} \ne{0}}[/latex] | [latex]{\large {x}^{-4}=\dfrac{1}{{x}^{4}}}[/latex] |
Product Rule to Multiply Exponential Expressions
What happens if you multiply two numbers in exponential form with the same base? Consider the expression [latex]{2}^{3}{2}^{4}[/latex]. Exponents are repeated multiplication so we can Expand each exponent as [latex]\left(2\cdot2\cdot2\right)\left(2\cdot2\cdot2\cdot2\right)[/latex] or [latex]2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2[/latex]. In exponential form, you would write the product as [latex]2^{7}[/latex]. Notice that [latex]7[/latex] is the sum of the original two exponents, [latex]3[/latex] and [latex]4[/latex].
What about [latex]{x}^{2}{x}^{6}[/latex]? This can be written as [latex]\left(x\cdot{x}\right)\left(x\cdot{x}\cdot{x}\cdot{x}\cdot{x}\cdot{x}\right)=x\cdot{x}\cdot{x}\cdot{x}\cdot{x}\cdot{x}\cdot{x}\cdot{x}[/latex] or [latex]x^{8}[/latex]. And, once again, [latex]8[/latex] is the sum of the original two exponents. This concept can be generalized in the following way:
The Product Rule for Exponents
For any number [latex]a[/latex] and any integers [latex]m[/latex] and [latex]n[/latex],
[latex]\left(a^{m}\right)\left(a^{n}\right) = a^{m+n}[/latex].
If [latex]m[/latex], [latex]n[/latex], or [latex]m+n[/latex] is [latex]0[/latex] or negative, then [latex]a[/latex] cannot be [latex]0[/latex].
To multiply exponential expressions with the same base, add the exponents.
Example
Write each of the following products with a single base. Do not simplify further.
- [latex]{t}^{5}\cdot {t}^{3}[/latex]
- [latex]{-3x^2}\cdot {4x^5}[/latex]
- [latex]{x}^{2}\cdot {x}^{5}\cdot {x}^{3}[/latex]
In the following video, you will see more examples of using the product rule for exponents to simplify expressions.
Quotient Rule to Divide Exponential Expressions
Let us look at dividing terms containing exponential expressions. What happens if you divide two numbers in exponential form with the same base? Consider the following expression: [latex]\dfrac{7^5}{7^2}[/latex]. You can rewrite the expression as [latex]\dfrac{7\cdot 7\cdot 7\cdot 7\cdot 7}{7\cdot 7}[/latex].
Then you can divide out the common factors of 7 in the numerator and denominator:
[latex]\require{color}\dfrac{\color{red}\cancel{\color{black}7} \color{black} \cdot \color{red}\cancel{\color{black}7} \color{black} \cdot 7 \cdot 7 \cdot 7}{\color{red}\cancel{\color{black}7} \color{black} \cdot \color{red}\cancel{\color{black}7 \color{black}}}[/latex]
Finally, this expression can be rewritten as [latex]7^{3}[/latex] using exponential notation. Notice that the exponent, [latex]3[/latex], is the difference between the two exponents in the original expression, [latex]5[/latex] and [latex]2[/latex]. So, [latex]\dfrac{7^5}{7^2}=7^{5-2}=7^{3}[/latex].
Be careful that you subtract the exponent in the denominator from the exponent in the numerator. So, to divide two exponential expressions with the same base, subtract the exponents.
The Quotient (Division) Rule for Exponents
For any non-zero number [latex]a[/latex] and any integers [latex]m[/latex] and [latex]n[/latex]:
[latex]\displaystyle \dfrac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}}, a \ne 0[/latex]
To divide exponential expressions with the same base, subtract the exponents.
Example
Write each of the following products with a single base. Do not simplify further.
- [latex]\dfrac{{\left(-2\right)}^{14}}{{\left(-2\right)}^{9}}[/latex]
- [latex]\dfrac{{t}^{23}}{{t}^{15}}[/latex]
In the following video, you will see more examples of using the quotient rule for exponents.
Raise Exponential Expressions to Powers
Another word for exponent is power. You have likely seen or heard an example such as [latex]3^5[/latex] can be described as [latex]3[/latex] raised to the [latex]5[/latex]th power. In this section we will further expand our capabilities with exponents. We will learn what to do when an expression with a power is raised to another power and what to do when two numbers or variables are multiplied and both are raised to a power. We will also learn what to do when numbers or variables that are divided are raised to a power. We will begin by raising exponential expressions to powers.
Let us simplify [latex]\left(5^{2}\right)^{4}[/latex].
In this case, [latex]\left(5^{2}\right)^{4}[/latex] indicates that the quantity [latex]5^2[/latex] is raised to the fourth power , so you multiply [latex]5^{2}[/latex] four times: [latex]\left(5^{2}\right)^{4}=5^{2}\cdot5^{2}\cdot5^{2}\cdot5^{2}=5^{8}[/latex] (using the Product Rule—add the exponents).
We saw above that the answer is [latex]5^{8}[/latex]. Notice that the new exponent is the same as the product of the original exponents: [latex]2\cdot4=8[/latex]. So, [latex]\left(5^{2}\right)^{4}=5^{2\cdot4}=5^{8}[/latex] (which equals [latex]390,625[/latex] if you do the multiplication).
Likewise, [latex]\left(x^{4}\right)^{3}=x^{4\cdot3}=x^{12}[/latex].
This leads to the Power Rule for Exponents. To simplify a power of a power, you multiply the exponents, keeping the base the same. For example, [latex]\left(2^{3}\right)^{5}=2^{15}[/latex].
The Power Rule for Exponents
For any real number [latex]a[/latex] and integers [latex]m[/latex] and [latex]n[/latex]:
[latex]\left(a^{m}\right)^{n}=a^{m\cdot{n}}[/latex].
If [latex]m[/latex] or [latex]n[/latex] is [latex]0[/latex] or negative, then [latex]a[/latex] must not be [latex]0[/latex].
When raising an exponential expression to a power, keep the base the same and multiply the exponents.
Take a moment to contrast in your mind how the power rule for exponents is different from the product rule for exponents. With the power rule you are multiplying the exponents but with the product rule you are adding the exponents.
Example
Write each of the following products with a single base. Do not simplify further.
- [latex]{\left({x}^{2}\right)}^{7}[/latex]
- [latex]{\left({\left(-3\right)}^{5}\right)}^{11}[/latex]
In the following video, you will see more examples of using the power rule to simplify expressions with exponents.
Be careful to distinguish between uses of the product rule and the power rule.
- Using the product rule: When multiplying expressions with exponents with the same base, keep the base, add the exponents.
- Using the power rule: When raising an expression with an exponent to a power, keep the base and multiply the exponents.
Zero Exponent Rule
Above when we used the quotient rule we had expressions for which [latex]m[/latex] is larger than [latex]n[/latex] so that the difference [latex]m-n[/latex] would never be zero or negative.
What would happen if [latex]m[/latex] and [latex]n[/latex] were equal? In this case, we would use the zero exponent rule of exponents to simplify the expression to [latex]1[/latex]. To see how this is done, let us begin with an example.
[latex]\require{color}\dfrac{t^8}{t^8}=\dfrac{\color{red}\cancel{\color{black}{t^8}}}{\color{red}\cancel{\color{black}{t^8}}}=1[/latex]
If we were to simplify the original expression using the quotient rule, we would have: [latex]\dfrac{{t}^{8}}{{t}^{8}}={t}^{8 - 8}={t}^{0}[/latex]
For both methods of simplifying to be true, then [latex]{t}^{0}=1[/latex]. This is true for any nonzero real number, or any variable representing a nonzero real number. The sole exception is the expression [latex]{0}^{0}[/latex]. This appears later in more advanced courses, but for now, we will consider the value to be indeterminate.
The Zero Exponent Rule for Exponents
For any nonzero real number [latex]a[/latex], the zero exponent rule of exponents states that
Any number (except [latex]0[/latex]) raised to the zero power is [latex]1[/latex].
Example
Simplify each expression using the zero exponent rule of exponents.
- [latex]-3^2\cdot{(-5x^2)}^{0}[/latex]
- [latex]\dfrac{-3{x}^{5}}{{x}^{5}}[/latex]
In the following video, you will see more examples of simplifying expressions whose exponents may be zero.
Negative Exponent Rule
Can we simplify [latex]\dfrac{{h}^{3}}{{h}^{5}}[/latex]?
When [latex]n\ is\ larger\ than\ m[/latex], the difference [latex]m-n[/latex] is negative. We can use the negative rule of exponents to simplify the expression so that it is easier to understand.
Let’s look at an example to clarify this idea. Given the expression: [latex]\dfrac{{h}^{3}}{{h}^{5}}[/latex].
Let’s expand the numerator and denominator and then divide out the common factors to simplify.
[latex]\begin{align} \dfrac{h^3}{h^5} &= \dfrac{h\cdot h\cdot h}{h\cdot h\cdot h\cdot h\cdot h}\\ &= \dfrac{{\color{red}\cancel{\color{black}{h}}}\cdot{\color{red}\cancel{\color{black}{h}}}\cdot{\color{red}\cancel{\color{black}{h}}}} {{\color{red}\cancel{\color{black}{h}}}\cdot{\color{red}\cancel{\color{black}{h}}}\cdot{\color{red}\cancel{\color{black}{h}}}\cdot h\cdot h}\\ &= \dfrac{1}{h\cdot h}\\ &= \dfrac{1}{h^2} \end{align}[/latex]
Or, we can simplify using the Quotient Rule:
[latex]\begin{array}{ccc}\hfill \dfrac{{h}^{3}}{{h}^{5}}& =& {h}^{3 - 5}\hfill \\ & =& \text{ }{h}^{-2}\hfill \end{array}[/latex]
Putting the answers together, we have [latex]{h}^{-2}=\dfrac{1}{{h}^{2}}[/latex]. This is true for any nonzero real number, or any variable representing a nonzero real number.
The Negative Rule of Exponents
For any nonzero real number [latex]a[/latex] and any integer [latex]n[/latex], the negative rule of exponents states that
When the exponent is negative, write the reciprocal of the base raised to the positive exponent.
Example
Simplify. Write answers with positive exponents.
- [latex]\dfrac{y^3}{{y}^{-4}}[/latex]
- [latex]{-3}^{-2}[/latex]
- [latex]\dfrac{{(2b) }^{3}}{{(2b) }^{7}}[/latex]
- [latex]\dfrac{{z}^{2}\cdot z}{{z}^{4}}[/latex]
- [latex]\dfrac{{\left(-5{t}^{3}\right)}^{4}}{{\left(-5{t}^{3}\right)}^{7}}[/latex]
In the following video, you will see examples of simplifying expressions with negative exponents.
Combine Exponent Rules to Simplify Expressions
Now we will combine the use of the product and quotient rules to simplify expressions whose terms may have negative or zero exponents.
Example
Write each of the following products with a single base. Write answers with positive exponents.
- [latex]{b}^{2}\cdot {b}^{-8}[/latex]
- [latex]{\left(-x\right)}^{5}\cdot {\left(-x\right)}^{-5}[/latex]
- [latex]\dfrac{-7z}{{\left(-7z\right)}^{3}}[/latex]
The following video shows more examples of how to combine the use of the product and quotient rules to simplify expressions whose terms may have negative or zero exponents.
Finding the Power of a Product
To simplify the power of a product of two exponential expressions, we can use the power of a product rule of exponents which breaks up the power of a product of factors into the product of the powers of the factors.
For instance, consider [latex]{\left(pq\right)}^{3}[/latex].
We begin by using the associative and commutative properties of multiplication to regroup the factors.
[latex]\begin{array}{ccc}\hfill {\left(pq\right)}^{3}& =& \stackrel{3\text{ factors}}{{\left(pq\right)\cdot \left(pq\right)\cdot \left(pq\right)}}\hfill \\ & =& p\cdot q\cdot p\cdot q\cdot p\cdot q\hfill \\ & =& \stackrel{3\text{ factors}}{{p\cdot p\cdot p}}\cdot \stackrel{3\text{ factors}}{{q\cdot q\cdot q}}\hfill \\ & =& {p}^{3}\cdot {q}^{3}\hfill \end{array}[/latex]
In other words, [latex]{\left(pq\right)}^{3}={p}^{3}\cdot {q}^{3}[/latex].
The Power of a Product Rule for Exponents
For any real numbers [latex]a[/latex] and [latex]b[/latex] and any integer [latex]n[/latex], the power of a product rule of exponents states that
If [latex]n[/latex] is [latex]0[/latex] or negative, neither [latex]a[/latex] nor [latex]b[/latex] can be [latex]0[/latex].
When raising a product to a power, apply the exponent to each factor in the product. Then simplify the expression.
Example
Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.
- [latex]{\left(a{b}^{2}\right)}^{3}[/latex]
- [latex]{\left(-2{w}^{3}\right)}^{3}[/latex]
- [latex]{\left({j}^{3}{k}^{-2}\right)}^{-4}[/latex]
- [latex]\dfrac{1}{{\left(-2z\right)}^{4}}[/latex]
- [latex]{\left({e}^{-2}{f}^{3}\right)}^{7}[/latex]
Caution! Do not try to apply this rule to sums.
Think about the expression [latex]\left(2+3\right)^{2}[/latex]
Does [latex]\left(2+3\right)^{2}[/latex] equal [latex]2^{2}+3^{2}[/latex]?
No, it does not because of the order of operations!
[latex]\left(2+3\right)^{2}=5^{2}=25[/latex]
and
[latex]2^{2}+3^{2}=4+9=13[/latex]
Therefore, you can only use this rule when the numbers inside the parentheses are being multiplied or divided.
In the following video, we provide more examples of how to find the power of a product.
Finding the Power of a Quotient
To simplify the power of a quotient of two expressions, we can use the power of a quotient rule which states that the power of a quotient of factors is the quotient of the powers of the factors.
The Power of a Quotient Rule of Exponents
For any real numbers [latex]a[/latex] and [latex]b[/latex] and any integer [latex]n[/latex], the power of a quotient rule of exponents states that
If [latex]n[/latex] is negative or [latex]0[/latex], then [latex]a[/latex] cannot be [latex]0[/latex].
When raising a quotient to a power, apply the exponent to the numerator and denominator. Then simplify the expression.
Example
Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.
- [latex]{\left(\dfrac{4}{{z}^{11}}\right)}^{3}[/latex]
- [latex]{\left(\dfrac{-1}{{t}^{2}}\right)}^{27}[/latex]
- [latex]{\left(\dfrac{4xy^2}{x^3 {y}^{-2}}\right)}^{-2}[/latex]
The following video provides more examples of simplifying expressions using the power of a quotient and other exponent rules.
The video below works through some examples of simplifying expressions that contain powers and negative exponents.
Polynomial Functions and Expressions
You may see a resemblance between expressions and polynomials which we have been studying in this course. Polynomials are a special sub-group of mathematical expressions and equations. A polynomial is an expression consisting of the sum or difference of terms in which each term is a real number, a variable, or the product of a real number and variable(s) with non-negative integer exponent(s). Non negative integers are [latex]0, 1, 2, 3, 4[/latex], …
The basic building block of a polynomial is a monomial. A monomial is one term and can be a number, a variable, or the product of a number and variable(s) with an exponent. The number part of the term is called the coefficient.
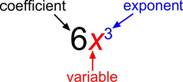
A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial. A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial. We can find the degree of a single variable polynomial by identifying the highest power of the variable that occurs in the polynomial. You will discuss the degree of multivariable polynomials in later courses. The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers on a specified variable are descending, meaning the power of the term decreases for each succeeding term, we say that it is in standard form. It is important to note that polynomials only have integer exponents.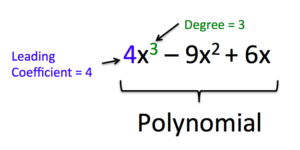
Example
For the following polynomials, identify the degree, the leading term, and the leading coefficient.
- [latex]3+2{x}^{2}-4{x}^{3}[/latex]
- [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
- [latex]6p-{p}^{3}-2[/latex]
In the following video, we will identify the terms, leading coefficient, and degree of a polynomial.
Add and Subtract Polynomials
Recall from previous courses that we can add and subtract polynomials by combining like terms which are terms that contain the same variables raised to the same exponents. For example, [latex]5{x}^{2}[/latex] and [latex]-2{x}^{2}[/latex] are like terms and can be added to get [latex]3{x}^{2}[/latex], but [latex]3x[/latex] and [latex]3{x}^{2}[/latex] are not like terms; therefore, they cannot be added.
Example
Find the sum.
[latex]\left(12{x}^{2}+9x - 21\right)+\left(4{x}^{3}+8{x}^{2}-5x+20\right)[/latex]
When you subtract polynomials, you will still be looking for like terms to combine, but you will need to pay attention to the sign of the terms you are combining. In the following example, we will show how to distribute the negative sign to each term of a polynomial that is being subtracted from another.
Example
Find the difference.
[latex]\left(7{x}^{4}-{x}^{2}+6x+1\right)-\left(5{x}^{3}-2{x}^{2}+3x+2\right)[/latex]
In the following video, we show more examples of adding and subtracting polynomials.
Multiplying Polynomials
Multiplying polynomials is a bit more challenging than adding and subtracting polynomials. We must use the distributive property to multiply each term in the first polynomial by each term in the second polynomial. We then combine like terms.
The following video will provide you with examples of using the distributive property to find the product of monomials and polynomials.
Multiplying Two Binomials
You can use the distributive property when multiplying two binomials. In other words, multiply each term in the first binomial by each term in the second.
EXAMPLE
Simplify. [latex](x+4)(x-2)[/latex]
Using FOIL to Multiply Binomials
The acronym FOIL (First, Outer, Inner, Last) is a memory device to multiply two binomials. It is called the FOIL method because we multiply the
First terms, Outer terms, Inner terms, and Last terms.
The FOIL method arises out of the distributive property. We are simply multiplying each term of the first binomial by each term of the second binomial and then combining like terms. FOIL method only works when multiplying a binomial by another binomial.
Example
Use FOIL to find the product. [latex](2x-18)(3x+3)[/latex]
In the following video, we show an example of how to use the FOIL method to multiply two binomials. Remember that the FOIL method is only used when multiplying two binomials.
Using the Box Method to Multiply Polynomials
Another method you can use to multiply binomials is the Box Method, where you can use a table to organize the terms as shown below. Let’s use the Box Method to multiply [latex](4x-5)[/latex] and [latex](2x+7)[/latex]. Write one polynomial factor across the top and the other down the side. For each box in the table, multiply the term for that row by the term for that column. Then combine like terms to simplify. Notice that we need to keep the sign on each term when we write it in the table.
| [latex]4x[/latex] | [latex]-5[/latex] | |
| [latex]2x[/latex] | [latex]8{x}^{2}[/latex] | [latex]-10x[/latex] |
| [latex]+7[/latex] | [latex]28x[/latex] | [latex]-35[/latex] |
[latex]\begin{align} \require{color} (4x-5)(2x+7) &= 8{x}^{2}-10x +28x - 35 \\ &= 8{x}^{2}+18x - 35 &&\color{blue}{\text{combine like terms}}\end{align}[/latex]
Multiplying a Binomial with a Trinomial
Another type of polynomial multiplication problem is the product of a binomial and trinomial. Although the FOIL method cannot be used since there are more than two terms in a trinomial, you still use the distributive property to organize the individual products. Using the distributive property, each term in the binomial must be multiplied by each of the terms in the trinomial. For this example, we will show you two ways to organize all of the terms that result from multiplying polynomials with more than two terms. The most important part of the process is finding a way to organize terms.
Example
Find the product using the Distributive Property. [latex]\left(3x-6\right)\left(5x^{2}+3x+10\right)[/latex]
We will now rework this example using the Box Method. The Box Method is good to use when you are multiplying a binomial by a trinomial because it can help you keep track of all of the terms involved.
ExAMPLE
Find the product using the Box Method. [latex](3x-6)(5{x}^{2}+3x+10)[/latex]
Let’s look at another example where we are multiplying a binomial with a trinomial. Pay attention to the signs on the terms. Forgetting a negative sign is the easiest mistake to make in this case.
Example
Find the product using the Distributive Property.
[latex]\left(2x+1\right)\left(3{x}^{2}-x+4\right)[/latex]
We will rework the above example using the Box Method
ExAMPLE
Find the product using the Box Method.
[latex]\left(2x+1\right)\left(3{x}^{2}-x+4\right)[/latex]
In the following video, we show more examples of multiplying polynomials.
Candela Citations
- Ex: Multiplying Using the Distributive Property. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/bwTmApTV_8o. License: CC BY: Attribution
- Multiply Binomials Using An Area Model and Using Repeated Distribution. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/u4Hgl0BrUlo. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Multiply Binomials Using the FOIL Acronym. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/_MrdEFnXNGA. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay, et al.. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution. License Terms: Download for free at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
- Ex: Adding and Subtracting Polynomials. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/jiq3toC7wGM. License: CC BY: Attribution
- Ex: Polynomial Multiplication Involving Binomials and Trinomials. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/bBKbldmlbqI. License: CC BY: Attribution





