Learning Outcomes
- Solve applications using the Pythagorean Theorem
- Compute the distance between two points using the Distance Formula
- Find the midpoint between two points using the Midpoint Formula
The Pythagorean Theorem
The Pythagorean theorem is a statement about the sides of a right triangle. One of the angles of a right triangle is always equal to [latex]90[/latex] degrees. This angle is the right angle. The two sides next to the right angle are called the legs and the other side is called the hypotenuse. The hypotenuse is the side opposite the right angle, and it is always the longest side.
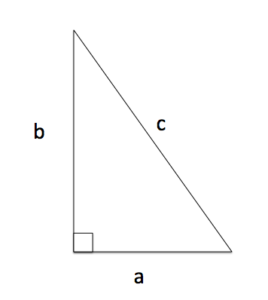
A right triangle with sides labeled.
The Pythagorean theorem is often used to find unknown lengths of the sides of right triangles. If the hypotenuse is labeled [latex]c[/latex], and the other two sides [latex]a[/latex] and [latex]b[/latex] as in the image on the left, The Pythagorean Theorem states that
[latex]a^2+b^2=c^2[/latex]
If we are given any two side lengths of a right triangle, we can use the Pythagorean Theorem to solve for the remaining side.
Consider an example where [latex]a=5[/latex] and [latex]b=7.[/latex] We can write
[latex]\begin{align}5^2+7^2&=c^2\\25+49&=c^2\\74&=c^2\end{align}[/latex]
We would normally solve a quadratic equation such as this by factoring, but [latex]74[/latex] is not a perfect square, so none of our factoring techniques will be successful. We need to introduce a new technique – the square root property.
SQUARE ROOT PROPERTY
If [latex]x^2=n[/latex] where [latex]n[/latex] is positive, then [latex]x=\sqrt{n}[/latex] or [latex]x=-\sqrt{n}.[/latex]
The reason we get two solutions is because of the observation earlier in this chapter that every positive number has two square roots – the principle root and the negative root. Squaring either of them results in a positive quantity. In this section we will be working with lengths and distances, so only the positive answer makes sense. In the next chapter we will need both solutions.
The length of the hypotenuse is [latex]c=\sqrt{74}\approx 8.60[/latex] The final answer can either be stated as a simplified radical or approximated as a decimal, depending on the prompt of the problem.
Try this example yourself.
Example
A triangle has one leg of length [latex]6[/latex] and hypotenuse of length [latex]12[/latex]. Find the length of the remaining leg. Write the answer both in simplified exact form and as an approximation rounded to two decimal places.
Many application problems involve finding the lengths of sides in a right triangle.
Example
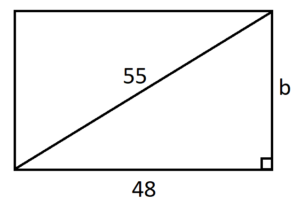
TV screens are typically measured by the length of their diagonal from one corner to the opposite corner. Suppose that a [latex]55[/latex] inch TV has a width of [latex]48[/latex] inches. How tall is the screen? Round your answer to the nearest tenth of an inch.
Sometimes we can solve when multiple side lengths are unknown, if we know a relationship between the sides.
Example
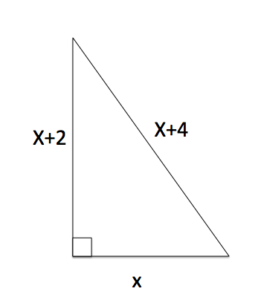
A right triangle has one leg with length [latex]x[/latex], another whose length is greater by two, and the length of the hypotenuse is greater by four. Find the lengths of the sides of the triangle. Use the image below.
Here is a video illustrating the same concept.
The Distance Formula
Derived from the Pythagorean Theorem, the distance formula is used to find the distance between two points in the plane. Consider points [latex](x_1,y_1)[/latex] and [latex](x_2,y_2).[/latex] The diagram below shows the desired distance [latex]d[/latex] between them, which is the hypotenuse of a right triangle with sides parallel to the axes. We can find the lengths of the legs by finding the horizontal distance [latex]x_2-x_1[/latex] and vertical distance [latex]y_2-y_1[/latex] between the points. We use absolute values to make sure that these differences are nonnegative.
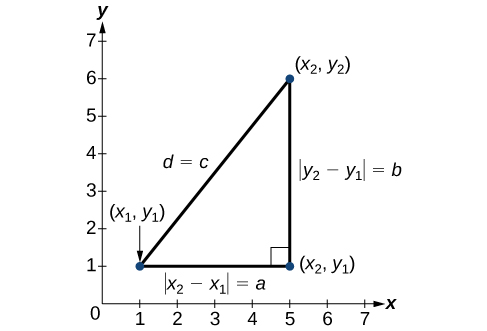
Using these three side lengths in the Pythagorean Theorem, we obtain
[latex]\begin{align}d^2&={\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}\\ d&=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}\end{align}[/latex]
Note that we ended up ignoring the absolute values because squaring always results in a nonnegative quantity anyway. Here is the distance formula stated formally:
The distance formula
The distance between the two points [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex] is given by
Example
Find the distance between the points [latex]\left(-3,-1\right)[/latex] and [latex]\left(2,3\right)[/latex]. Write the answer both in exact form and as an approximation rounded to 2 decimal places.
Try It YOURSELF
Example
A subway takes passengers from a station at 9th street East, 3rd street North in a straight line to another station at 12th street East, 10th street North. If each city block (for example, 3rd East to 4th East) is one tenth of a mile, how far is it between the two stations to the nearest hundredth of a mile?
The Midpoint Formula
When the endpoints of a line segment are known, we can find the point midway between them. This point is known as the midpoint and the formula is known as the midpoint formula.
THE MIDPOINT FORMULA
Given the endpoints of a line segment, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the midpoint is
[latex]\displaystyle M=\left(\dfrac{{x}_{1}+{x}_{2}}{2},\dfrac{{y}_{1}+{y}_{2}}{2}\right)[/latex]
It makes sense that since the midpoint is halfway from Point [latex]1[/latex] to Point [latex]2,[/latex] it should be halfway in both the [latex]x[/latex] direction and the [latex]y[/latex] direction. The “midpoint” between two real numbers is called the average or mean. Thus, you can equivalently view the midpoint formula as
[latex]\displaystyle M=\left(\textsf{avg. of x coords, avg. of y coords}\right)[/latex]
A graphical view of a midpoint is shown below. Notice that the line segments on either side of the midpoint are congruent. If you like, you can verify that these two segments have equal length using the Distance Formula.
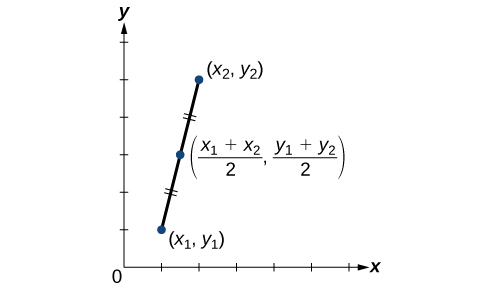
Example
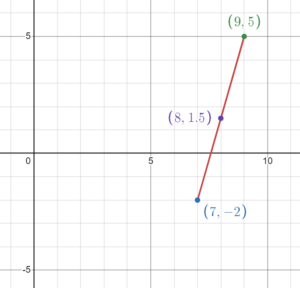
Find the midpoint of the line segment with the endpoints [latex]\left(7,-2\right)[/latex] and [latex]\left(9,5\right)[/latex].
Try It YOURSELF
Summary
The Pythagorean Theorem [latex]a^2+b^2=c^2[/latex] can be used to determine the side lengths of a right triangle with legs [latex]a, b[/latex] and hypotenuse [latex]c.[/latex] While solving the equation, we can use the Square Root Property: if [latex]x^2=n[/latex], then [latex]x=\sqrt{n}[/latex] (assuming [latex]x[/latex] is positive.)
The distance formula [latex]d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}[/latex] can find the distance between any two points in the plane. The midpoint formula [latex]M=\left(\dfrac{{x}_{1}+{x}_{2}}{2},\dfrac{{y}_{1}+{y}_{2}}{2}\right)[/latex] finds the midpoint of the line segment connecting any two points.
Candela Citations
- Pythagorean Theorem, Description and Examples. Provided by: Lumen Learning. License: CC BY: Attribution
- Factoring Application - Find the Lengths of Three Sides of a Right Triangle (Pythagorean Theorem). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/xeP5pRBqsNs. License: CC BY: Attribution
- Celestial Navigation Math. Authored by: TabletClass Math. Located at: https://www.youtube.com/watch?v=XWLZKmPU17M. License: All Rights Reserved. License Terms: Standard YouTube License
- Pythagorean Theorem. Provided by: Wikipedia. Located at: https://en.wikipedia.org/wiki/Pythagorean_theorem. License: CC BY-SA: Attribution-ShareAlike