Learning Outcomes
- Identify the radicand and the index of a radical expression.
- Simplify [latex]n[/latex]th roots of expressions that are perfect [latex]n[/latex]th powers.
- Evaluate [latex]n[/latex]th root functions.
- Determine the domain of a radical function from its equation and write in interval notation.
The most common root is the square root. First, we will define what square roots are and how you find the square root of a number. Then we will apply similar ideas to define and evaluate [latex]n[/latex]th roots.
Roots are the inverse of exponents, much like multiplication is the inverse of division. When you are trying to find a square root of a number (say, [latex]25[/latex]), you are trying to find a number that can be multiplied by itself to create that original number. In the case of [latex]25[/latex], you find that [latex]5\cdot5=25[/latex], so [latex]5[/latex] is a square root.
Square Roots
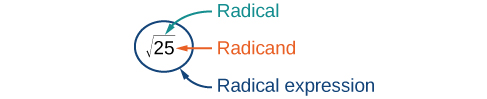
The symbol for square root is called a radical symbol and looks like this: [latex]\sqrt{\,\,\,}[/latex]. The expression [latex]\sqrt{25}[/latex] is read “square root of twenty-five” or “radical twenty-five.” The number that is written under the radical symbol is called the radicand.
The following table shows a few more examples of evaluating radicals.
| Radical | Name | Simplified Form |
|---|---|---|
| [latex]\sqrt{36}[/latex] | “Square root of thirty-six” | [latex]\sqrt{36}=\sqrt{6\cdot 6}=6[/latex] |
| [latex]\sqrt{\dfrac{1}{100}}[/latex] | “Square root of one hundredth” | [latex]\sqrt{\dfrac{1}{100}}=\sqrt{\dfrac{1}{10}\cdot \dfrac{1}{10}}=\dfrac{1}{10}[/latex] |
| [latex]\sqrt{0.16}[/latex] | “Square root of 16 hundredths” | [latex]\sqrt{0.16}=\sqrt{\dfrac{16}{100}}=\sqrt{\dfrac{4}{10}\cdot \dfrac{4}{10}}=\dfrac{4}{10}=\dfrac{2}{5}=0.4[/latex] |
| [latex]\sqrt{2}[/latex] | “Square root of 2” | [latex]\sqrt{2} \approx 1.414...[/latex] |
Note in the last example that there is no “nice” number that multiplies by itself to get [latex]2[/latex]. [latex]\sqrt{2}[/latex] is an example of an irrational number, which means it cannot be written as a quotient of two integers. As a decimal number it continues forever without repetition. A calculator is used to approximate its value as [latex]1.414[/latex], since [latex](1.414)^2 = 1.999396[/latex], which is close to [latex]2[/latex]. More decimal places can be used to get the result closer to [latex]2[/latex].
In our first example we will show you how to evaluate square roots.
Example
Simplify each expression.
- [latex]\sqrt{16}[/latex]
- [latex]\sqrt{25+144}[/latex]
- [latex]-\sqrt{\dfrac{9}{49}}[/latex]
- [latex]\sqrt{-9}[/latex]
The last example we showed leads to an important characteristic of square roots. You can only take the square root of numbers that are nonnegative.
SQUARE ROOTS OF NEGATIVE NUMBERS
We say that the square root of a negative number does not exist as a real number.
We will come back to this idea later when we discuss the domain of radical functions.
Principal Roots
Consider [latex]\sqrt{25}[/latex] again. You may realize that there is another number that, when multiplied by itself, also results in [latex]25[/latex]. That number is [latex]−5[/latex].
[latex]\begin{array}{r}5\cdot 5=25\\(-5)\cdot (-5)=25\end{array}[/latex]
By definition, the square root symbol always means to find the positive root called the principal root. So while [latex]5\cdot5[/latex] and [latex]−5\cdot−5[/latex] both equal [latex]25[/latex], only [latex]5[/latex] is the principal root. We say that [latex]−5[/latex] is called the negative root. We will never evaluate a radical as its negative root unless specifically asked to.
In the following video, we present more examples of how to find a principal square root.
Nth roots
We know that [latex]5^2=25, \text{ and }\sqrt{25}=5[/latex], but what if we want to “undo” [latex]5^3=125, \text{ or }5^4=625[/latex]? We can use higher order roots to answer these questions. For example, since [latex]5^3=125[/latex], we can say that [latex]\sqrt[3]{125}=5[/latex].
The [latex]n[/latex]th root of [latex]a[/latex] is written as [latex]\sqrt[n]{a}[/latex], where [latex]n[/latex] is a positive integer greater than or equal to [latex]2[/latex]. In the radical expression, [latex]n[/latex] is called the index of the radical.
Definition: nth Root
If [latex]a[/latex] is a real number with at least one [latex]n[/latex]th root, then the nth root of [latex]a[/latex], written as [latex]\sqrt[n]{a}[/latex], is the number with the same sign as [latex]a[/latex] that, when raised to the [latex]n[/latex]th power, equals [latex]a[/latex]. The index of the radical is [latex]n[/latex]. A square root has index of [latex]2[/latex], and the index number does not need to be written.
There is one interesting fact about cube roots that is not true of square roots. Negative numbers can have real number cube roots! What is the cube root of [latex]−8[/latex]? [latex]\sqrt[3]{-8}=-2[/latex] because [latex]-2\cdot -2\cdot -2=-8[/latex]. Remember, when you are multiplying an odd number of negative numbers, the result is negative! Here is a general fact about the existence of roots with negative radicands.
NTH ROOTS OF NEGATIVE NUMBERS
We say that an even index root of a negative number does not exist as a real number.
Odd index roots of negative numbers always exist as real numbers.
Example
Evaluate each of the following:
- [latex]\sqrt[3]{216}[/latex]
- [latex]\sqrt[5]{-32}[/latex]
- [latex]\sqrt[4]{81}[/latex]
- [latex]\sqrt[8]{-1}[/latex]
In the following video, we show more examples of how to evaluate [latex]n[/latex]th roots.
You can find the odd root of a negative number, but you cannot find the even root of a negative number. This means you can evaluate the radicals [latex]\sqrt[3]{-27},\ \sqrt[5]{-32}[/latex], and [latex]\sqrt[7]{-2187}[/latex], but the radicals [latex]\sqrt{-100},\ \sqrt[4]{-16}[/latex], and [latex]\sqrt[6]{-1}[/latex] are not real numbers. Let’s now state this using function vocabulary.
Radical Functions
The function [latex]f(x)=\sqrt{x}[/latex] is a radical function. We can evaluate it just like any other function by using a number or expression for the input. For example,
[latex]f(\color{green}{4}) = \sqrt{\color{green}{4}}=2[/latex].
As discussed earlier, we cannot use any negative number as an input in this function. However, every nonnegative number can be used as input (even if the radical must be approximated). Thus, we conclude that the domain of [latex]f[/latex] is all nonnegative numbers, or in interval notation [latex][0, \infty)[/latex]. We must also ensure a nonnegative radicand for any even index.
For the function [latex]f(x)=\sqrt[3]{x}[/latex], note that negative inputs are allowed. In fact, there is no real number which cannot be used as input. So the domain of [latex]f[/latex] is all real numbers, or [latex](-\infty, \infty)[/latex]. The same will be true of any radical function with an odd index.
Domain of Radical Functions
[latex]f(x)=\sqrt[n]{x}[/latex] has domain [latex][0, \infty)[/latex] if [latex]n[/latex] is even, and domain [latex](-\infty, \infty)[/latex] if [latex]n[/latex] is odd. When [latex]n[/latex] is even, we can solve for the domain by setting up an inequality to ensure the radicand is nonnegative: [latex]x \geq 0.[/latex]
As an example of the last statement, consider the domain of [latex]f(x)=\sqrt[4]{x-3}[/latex]. We cannot say the domain is [latex][0, \infty)[/latex] because if we use [latex]0[/latex] as input, the result would be [latex]f(0)=\sqrt[4]{0-3}=\sqrt[4]{-3}[/latex], which is not a real number. The key is that the radicand, [latex]\color{Green}{x-3}[/latex], is the quantity that must be nonnegative. We can state this with an inequality and solve:
[latex]\begin{align} \color{Green}{x-3} & \geq 0 \\ x &\geq 3 \end{align}[/latex]
So the domain of this function is the interval [latex][3, \infty)[/latex].
Example
Complete each of the following:
- Evaluate [latex]f(x) = \sqrt[3]{3x+3}[/latex] at [latex]x=-10[/latex]
- Determine the domain of [latex]f(x)=\sqrt{3x+7}[/latex]
- Determine the domain of [latex]f(x)=\sqrt[6]{5-x}[/latex]
- Determine the domain of [latex]f(x)=\sqrt[3]{5-x}[/latex]
Evaluating Radicals with Variables
Consider the expression [latex]\sqrt{{{x}^{2}}}[/latex]. This looks like it should be equal to [latex]x[/latex], right? Test some values for [latex]x[/latex] and see what happens.
In the chart below, look along each row and determine whether the value of [latex]x[/latex] is the same as the value of [latex]\sqrt{{{x}^{2}}}[/latex]. Where are they equal? Where are they not equal?
| [latex]x[/latex] | [latex]x^{2}[/latex] | [latex]\sqrt{x^{2}}[/latex] |
|---|---|---|
| [latex]−5[/latex] | [latex]25[/latex] | [latex]5[/latex] |
| [latex]−2[/latex] | [latex]4[/latex] | [latex]2[/latex] |
| [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| [latex]6[/latex] | [latex]36[/latex] | [latex]6[/latex] |
| [latex]10[/latex] | [latex]100[/latex] | [latex]10[/latex] |
Notice that in cases where [latex]x[/latex] is a negative number, [latex]\sqrt{x^{2}}\neq{x}[/latex]. The correct result of the square root was always positive since it was defined as the principal root. We can generally say that [latex]\sqrt{x^{2}}=\left|x\right|[/latex] because the absolute value will ensure the result represents the principal root.
Simplifying Radicals with Variables
When finding the square root of an expression that contains variables raised to an even power, remember that [latex]\sqrt{x^{2}}=\left|x\right|[/latex]. The absolute value signs are used for any even index.
Absolute values should not be used for odd index radicals. So [latex]\sqrt[n]{x^{n}}=x[/latex] if [latex]n[/latex] is odd.
If we already know that [latex]x[/latex] is nonnegative, then the absolute value signs are not necessary at all.
For example, [latex]\sqrt{9x^{2}}=\sqrt{(3x)^2}=\left|3x\right|[/latex], and [latex]\sqrt{16{{x}^{2}}{{y}^{2}}}=\sqrt{(4xy)^2}=\left|4xy\right|[/latex].
Example
Simplify each of the following:
- [latex]\sqrt{64y^2}[/latex]
- [latex]\sqrt{(2y+5)^2}[/latex]
- [latex]\sqrt[5]{32x^5y^5}[/latex]
- [latex]\sqrt{x^{12}}[/latex]
- [latex]-3x\sqrt{4x^2}[/latex], assuming [latex]x[/latex] is nonnegative
Summary
A square root of a number is a number which, when multiplied by itself, gives the original number. Principal square roots are always positive or zero. In general, an [latex]n[/latex]th root is a number which, when raised to the [latex]n[/latex]th power, gives the original number. You can only take an even root of numbers that are greater than or equal to [latex]0[/latex]. When simplifying radical expressions with variables, be careful to use absolute values when the index is even.
Candela Citations
- Simplify a Variety of Square Expressions (Simplify Perfectly). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/2cWAkmJoaDQ. License: CC BY: Attribution
- Simplify Cube Roots (Perfect Cube Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/9Nh-Ggd2VJo. License: CC BY: Attribution
- Simplify Perfect Nth Roots. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/vA2DkcUSRSk. License: CC BY: Attribution
- Approximate a Square Root to Two Decimal Places Using Trial and Error. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/iNfalyW7olk. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
- Precalculus. Authored by: Abramson, Jay. Provided by: Open Stax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution. License Terms: Download for free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface
