Learning Outcomes
- Rewrite expressions with rational exponents using radical notation.
- Rewrite radical expressions using rational exponents.
- Rewrite expressions containing negative exponents using positive rational exponents.
- Simplify expressions with rational exponents using the product and/or quotient rules.
- Simplify expressions with negative rational exponents using the product and/or quotient rules.
- Simplify expressions with rational exponents using the power rule.
- Simplify an expression involving a product and/or quotient raised to a rational exponent.
- Simplify radical expressions by rewriting using rational exponents.
When we write a radical expression like [latex]\sqrt{3}[/latex], what we mean is that [latex]\sqrt{3}[/latex] is the number such that squaring it results in 3. In other words,
[latex]\left(\sqrt{3}\right)^2 = 3[/latex]
However, something similar can happen when applying the Power Rule of exponents, [latex]\left(a^m\right)^n = a^{m\cdot n}[/latex]:
[latex]\left(3^{\frac{1}{2}}\right)^2 =3^{\frac{1}{2}\cdot 2} = 3^1 = 3[/latex]
As long as it is legal to use the exponent properties with rational exponents, what we have shown is that [latex]\sqrt{3}=3^{\frac{1}{2}}[/latex], since squaring both of them results in the same number! This suggests a possible interpretation of a [latex]\dfrac{1}{2}[/latex] exponent:
RATIONAL EXPONENTS
We define [latex]a^{\frac{1}{2}} = \sqrt{a}[/latex].
Using similar logic as above, we can similarly define [latex]a^{\frac{1}{n}} = \sqrt[n]{a}[/latex] for any positive integer [latex]n \geq 2[/latex] since raising both sides to the [latex]n[/latex]th power results in [latex]a[/latex]. If [latex]a[/latex] is negative and [latex]n[/latex] is even, these expressions are not real numbers.
We can restate the above box as “the denominator of the exponent is the index of the radical.”
Having difficulty imagining a number being raised to a rational power? They may be hard to get used to, but rational exponents can actually help simplify some problems. Writing radicals with rational exponents will come in handy when we discuss techniques for simplifying more complex radical expressions.
Write an Expression with a Rational Exponent as a Radical
Radicals and rational exponents are alternate ways of expressing the same thing. In the table below, we show equivalent ways to express radicals: with a radical, with a rational exponent, and as a principal root.
|
Radical Form |
Exponent Form |
Principal Root |
|---|---|---|
| [latex]\sqrt{16}[/latex] | [latex]{{16}^{\tfrac{1}{2}}}[/latex] | [latex]4[/latex] |
| [latex]\sqrt{25}[/latex] | [latex]{{25}^{\tfrac{1}{2}}}[/latex] | [latex]5[/latex] |
| [latex]\sqrt{100}[/latex] | [latex]{{100}^{\tfrac{1}{2}}}[/latex] | [latex]10[/latex] |
Let us look at some more examples, but this time with cube roots. Remember, cubing a number raises it to the power of three. Notice that in the examples in the table below, the denominator of the rational exponent is the number [latex]3[/latex].
|
Radical Form |
Exponent Form |
Principal Root |
|---|---|---|
| [latex]\sqrt[3]{8}[/latex] | [latex]{{8}^{\tfrac{1}{3}}}[/latex] | [latex]2[/latex] |
| [latex]\sqrt[3]{125}[/latex] | [latex]{{125}^{\tfrac{1}{3}}}[/latex] | [latex]5[/latex] |
| [latex]\sqrt[3]{1000}[/latex] | [latex]{{1000}^{\tfrac{1}{3}}}[/latex] | [latex]10[/latex] |
These examples help us model a relationship between radicals and rational exponents: namely, that the nth root of a number can be written as either [latex]\sqrt[n]{x}[/latex] or [latex]{{x}^{\frac{1}{n}}}[/latex].
|
Radical Form |
Exponent Form |
|---|---|
| [latex]\sqrt{x}[/latex] | [latex]{{x}^{\tfrac{1}{2}}}[/latex] |
| [latex]\sqrt[3]{x}[/latex] | [latex]{{x}^{\tfrac{1}{3}}}[/latex] |
| [latex]\sqrt[4]{x}[/latex] | [latex]{{x}^{\tfrac{1}{4}}}[/latex] |
| … | … |
| [latex]\sqrt[n]{x}[/latex] | [latex]{{x}^{\tfrac{1}{n}}}[/latex] |
We can write radicals with rational exponents, and as we will see when we simplify more complex radical expressions, this can make things easier. A big advantage is that rewriting radicals as rational exponents could potentially allow us to use our exponent properties to simplify them.
Rational Exponents Whose Numerator is Not Equal to One
All of the numerators for the rational exponents in the examples above were [latex]1[/latex]. Suppose we wanted to make sense of [latex]3^{\frac{2}{3}}[/latex]. We can again use the Power Rule of exponents (in two different ways!) to rewrite this expression:
[latex]\begin{align} =&3^{^{\frac{2}{3}}}=3^{\frac{1}{3}\cdot 2}=\left(3^{\frac{1}{3}}\right)^2=(\sqrt[3]{3})^2 \textsf{ ... OR ...}\\ =&3^{\frac{2}{3}}=3^{2\cdot \frac{1}{3}}=\left(3^{2}\right)^{\frac{1}{3}}=\sqrt[3]{3^2}\end{align}[/latex]
This leads us to our main rule for this section:
GENERAL RATIONAL EXPONENTS
The two forms [latex]\sqrt[n]{a^{m}}[/latex] and [latex]a^{\frac{m}{n}}[/latex] are equivalent. Both of these are also equivalent to [latex](\sqrt[n]{a})^m[/latex] as long as [latex]\sqrt[n]{a}[/latex] exists.
This rule generalizes and includes the previous rule, since if [latex]m=1[/latex] then the rule says the same thing.
Here are some examples of using our new rule:
|
Radical |
Exponent |
|---|---|
| [latex]\sqrt{9}[/latex] | [latex]9^{\frac{1}{2}}[/latex] |
| [latex]\sqrt[3]{{{9}^{2}}}[/latex] | [latex]9^{\frac{2}{3}}[/latex] |
| [latex]\sqrt[4]{9^{3}}[/latex] | [latex]9^{\frac{3}{4}}[/latex] |
| [latex]\sqrt[5]{9^{2}}[/latex] | [latex]9^{\frac{2}{5}}[/latex] |
| … | … |
| [latex]\sqrt[n]{9^{x}}[/latex] | [latex]9^{\frac{x}{n}}[/latex] |
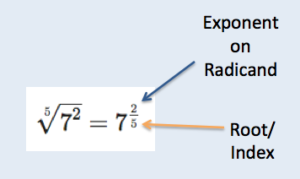
To rewrite a radical using a rational exponent, the power to which the radicand is raised becomes the numerator and the index becomes the denominator.
Let’s practice this concept with a few examples.
Example
Rewrite the expressions using a radical.
- [latex]{x}^{\frac{1}{7}}[/latex]
- [latex]{5}^{\frac{4}{7}}[/latex]
- [latex]{9}^{\frac{3}{2}}[/latex] (Also simplify the result)
- [latex]{{(2x)}^{^{\frac{1}{3}}}}[/latex]
- [latex]2{{x}^{^{\frac{1}{3}}}}[/latex]
Notice in the last two examples that use of parentheses can change how the exponent is applied. Remember from working with polynomials that [latex]2x^3[/latex] means only to cube the [latex]x[/latex] and not the coefficient [latex]2.[/latex]
Example
Rewrite each expression using a rational exponent.
- [latex]\sqrt[4]{81}[/latex]
- [latex]4\sqrt[3]{xy}[/latex]
- [latex]\sqrt[6]{{{a}^{3}}}[/latex]
- [latex]\sqrt[12]{16^3}[/latex]
In the following video, we show more examples of writing radical expressions with rational exponents and expressions with rational exponents as radical expressions.
We will use this notation later, so come back for practice if you forget how to write a radical with a rational exponent.
Using Exponent Properties
We have implied a few times that we would like our exponent properties to work in general for all rational numbers, and not just for integers like they did in Section 3.1. Fortunately, this will be the case and all of our rules work consistently with radicals if we define it this way. Let’s state this very important fact here.
EXPONENT PROPERTIES
All of our exponent properties work for rational exponents (before, we only said they were true for integers).
In addition, since radicals are equivalent to rational exponents, this means that
Whenever we want to investigate or simplify radicals,
we often convert to exponents and use exponent properties!
We will make use of this philosophy in the coming sections.
For now, here is a reminder of our previous exponent properties (which now work for rational exponents):
| Name | Property | Example |
|---|---|---|
| Product Rule | [latex]{\large a^{m}\cdot{a}^{n}=a^{m+n}}[/latex] | [latex]{\large x^{1/3}\cdot{x}^{1/2}=x^{1/3+1/2}=x^{5/6}}[/latex] |
| Quotient Rule | [latex]{\large \dfrac{a^{m}}{{a}^{n}}=a^{m-n}}[/latex] | [latex]{\large \dfrac{x^{1/2}}{{x}^{1/3}}=x^{1/2-1/3}=x^{1/6}}[/latex] |
| Power Rule | [latex]{\large \left(a^{m}\right)^{n}=a^{m\cdot{n}}}[/latex] | [latex]{\large \left(x^{1/5}\right)^{2}=x^{2\cdot{1/5}}=x^{2/5}}[/latex] |
| Power of a Product Rule | [latex]{\large \left(ab\right)^{n}=a^{n}\cdot b^{n}}[/latex] | [latex]{\large \left(2y\right)^{1/2}=2^{1/2}\cdot y^{1/2}}[/latex] |
| Power of a Quotient Rule | [latex]{\large \left(\dfrac{a}{b}\right)^{n}=\dfrac{{a}^{n}}{{b}^{n}}}[/latex] | [latex]{\large \left(\dfrac{x}{3}\right)^{1/3}=\dfrac{{x}^{1/3}}{{3}^{1/3}}}[/latex] |
| Negative Exponent Rule | [latex]{\large {a}^{-n}=\dfrac{1}{{a}^{n}}}[/latex] | [latex]{\large {x}^{-1/2}=\dfrac{1}{{x}^{1/2}}}[/latex] |
Here are a few examples of using our exponent properties to simplify a rational expression with many factors. This is similar to what we’ve done before with integer exponents, but now we use rational exponents. Such an expression is considered fully simplified when three things are done.
Simplifying requirements
To simplify a rational expression involving factors with exponents, you must use Properties of Exponents to do the following (in any order):
- Apply all powers, for example [latex]\left(x^2y\right)^3=\left(x^2\right)^3y^3=x^6y^3[/latex]
- Combine so each variable appears only once
- Rewrite all negative exponents in an equivalent form with positive exponents
Example
Simplify each expression. Assume all variables represent positive quantities and write your final answer using no negative exponents.
- [latex]\left(\frac{x^{2/5}}{y^{4/3}}\right)^{-1/3}[/latex]
- [latex]\frac{x^{1/5}y^{1/2}(x^{1/2}y^{-1})^{-7/5}}{x^{3/2}y^{8/5}}[/latex]
In the next example, we take advantage of exponent properties to rewrite and simplify an expression with multiple radicals. This is a preview of the next few sections, where we will use exponent properties frequently to work with radicals.
Example
Simplify. Write your answer in radical notation. [latex]\sqrt[3]{\sqrt[4]{x}}[/latex]
Summary
Any radical in the form [latex]\sqrt[n]{a^{x}}[/latex] can be written using a rational exponent in the form [latex]a^{\frac{x}{n}}[/latex]. Rewriting radicals using rational exponents can be useful when simplifying some radical expressions. When working with rational exponents, remember that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
Candela Citations
- Write Expressions Using Radicals and Rational Exponents. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/5cWkVrANBWA. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
- Precalculus. Authored by: Abramson, Jay. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: Public Domain: No Known Copyright. License Terms: Dwonload fro free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface
