Learning Outcomes
- Solve quadratic equations using the quadratic formula for equations with integer, rational, irrational, or complex number solutions.
- Find [latex]x[/latex]-intercepts (if they exist) of quadratic functions using the quadratic formula.
You can solve any quadratic equation by completing the square—rewriting part of the equation as a perfect square trinomial. If you complete the square on the generic equation [latex]ax^{2}+bx+c=0[/latex] and then solve for [latex]x[/latex], you find that [latex]x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}[/latex]. This equation is known as the Quadratic Formula.
We can derive the quadratic formula by completing the square. First, assume that the leading coefficient is positive; if it is negative, we can multiply the equation by [latex]-1[/latex] and obtain a positive a. Given [latex]a{x}^{2}+bx+c=0[/latex], [latex]a\ne 0[/latex], we will complete the square as follows:
- First, move the constant term to the right side of the equal sign:
[latex]a{x}^{2}+bx=-c[/latex]
- As we want the leading coefficient to equal 1, divide through by a:
[latex]{x}^{2}+\frac{b}{a}x=-\frac{c}{a}[/latex]
- Then, find [latex]\frac{1}{2}[/latex] of the middle term, and add [latex]{\left(\frac{1}{2}\frac{b}{a}\right)}^{2}=\frac{{b}^{2}}{4{a}^{2}}[/latex] to both sides of the equal sign:
[latex]{x}^{2}+\frac{b}{a}x+\frac{{b}^{2}}{4{a}^{2}}=\frac{{b}^{2}}{4{a}^{2}}-\frac{c}{a}[/latex]
- Next, write the left side as a perfect square. Find the common denominator of the right side and write it as a single fraction:
[latex]{\left(x+\frac{b}{2a}\right)}^{2}=\frac{{b}^{2}-4ac}{4{a}^{2}}[/latex]
- Now, use the square root property, which gives
[latex]\begin{array}{l}x+\frac{b}{2a}=\pm \sqrt{\frac{{b}^{2}-4ac}{4{a}^{2}}}\hfill \\ x+\frac{b}{2a}=\frac{\pm \sqrt{{b}^{2}-4ac}}{2a}\hfill \end{array}[/latex]
- Finally, add [latex]-\frac{b}{2a}[/latex] to both sides of the equation and combine the terms on the right side. Thus,
[latex]x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex]
Here is a video explanation of the steps given above.
This formula is very helpful for solving quadratic equations that are difficult or impossible to factor, and using it can be faster than completing the square. The Quadratic Formula can be used to solve any quadratic equation of the form [latex]ax^{2}+bx+c=0[/latex].
The form [latex]ax^{2}+bx+c=0[/latex] is called standard form of a quadratic equation. Before solving a quadratic equation using the Quadratic Formula, it is vital that you be sure the equation is in this form. If you do not, you might use the wrong values for a, b, or c, and then the formula will give incorrect solutions.
Solving a Quadratic Equation using the Quadratic Formula
The Quadratic Formula will work with any quadratic equation, but only if the equation is in standard form, [latex]ax^{2}+bx+c=0[/latex]. To use it, follow these steps.
- Put the equation in standard form first.
- Identify the coefficients, a, b, and c. Be sure to include negative signs if the bx or c terms are subtracted.
- Carefully substitute the values noted in step [latex]2[/latex] into the equation. To avoid needless errors, use parentheses around each number input into the formula.
- Simplify as much as possible.
- Use the [latex]\pm[/latex] in front of the radical to separate the solution into two values: one in which the square root is added and one in which it is subtracted.
- Simplify both values to get the possible solutions.
That is a lot of steps. Let us try using the Quadratic Formula to solve a relatively simple equation first; then you will go back and solve it again using another factoring method.
Example
Use the Quadratic Formula to solve the equation [latex]x^{2}+4x=5[/latex].
You can check these solutions by substituting [latex]1[/latex] and [latex]−5[/latex] into the original equation.
| [latex]\begin{array}{r}x=1\\x^{2}+4x=5\\\left(1\right)^{2}+4\left(1\right)=5\\1+4=5\\5=5\end{array}[/latex] | [latex]\begin{array}{r}x=-5\\x^{2}+4x=5\,\,\,\,\,\\\left(-5\right)^{2}+4\left(-5\right)=5\,\,\,\,\,\\25-20=5\,\,\,\,\,\\5=5\,\,\,\,\,\end{array}[/latex] |
You get two true statements, so you know that both solutions work: [latex]x=1[/latex] or [latex]-5[/latex]. You have solved the equation successfully using the Quadratic Formula!
Watch this video to see an example of how to use the quadratic formula to solve a quadratic equation that has two real, rational solutions.
Sometimes, it may be easier to solve an equation using conventional factoring methods like finding number pairs that sum to one number (in this example, [latex]4[/latex]) and that produce a specific product (in this example [latex]−5[/latex]) when multiplied. The power of the Quadratic Formula is that it can be used to solve any quadratic equation, even those where finding number combinations will not work.
In the next video example, we show that the quadratic formula is useful when a quadratic equation has two irrational solutions that could not have been obtained by factoring.
Most of the quadratic equations you have looked at have two solutions, like the one above. The following example is a little different.
Example
Use the Quadratic Formula to solve the equation [latex]x^{2}-2x=6x-16[/latex].
Again, check using the original equation.
[latex]\begin{array}{r}x^{2}-2x=6x-16\,\,\,\,\,\\\left(4\right)^{2}-2\left(4\right)=6\left(4\right)-16\\16-8=24-16\,\,\,\,\,\,\\8=8\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
In the next example, we will show that some quadratic equations do not have real solutions. As we simplify with the quadratic formula, we may end up with a negative number under a square root, which, as we know, is not defined for real numbers.
Example
Use the Quadratic Formula to solve the equation [latex]x^2+x=-x-3[/latex]
We have seen two outcomes for solutions to quadratic equations; either there was one or two real number solutions. We have also learned that it is possible to take the square root of a negative number by using imaginary numbers. Having this new knowledge allows us to explore one more possible outcome when we solve quadratic equations. Consider this equation:
[latex]2x^2+3x+6=0[/latex]
Using the Quadratic Formula to solve this equation, we first identify a, b, and c.
[latex]a = 2,b = 3,c = 6[/latex]
We can place a, b and c into the quadratic formula and simplify to get the following result:
[latex]x=-\frac{3}{4}+\frac{\sqrt{-39}}{4}, x=-\frac{3}{4}-\frac{\sqrt{-39}}{4}[/latex]
Up to this point, we would have said that [latex]\sqrt{-39}[/latex] is not defined for real numbers and determine that this equation has no solutions. But, now that we have defined the square root of a negative number, we can also define a solution to this equation as follows.
[latex]x=-\frac{3}{4}+i\frac{\sqrt{39}}{4}, x=-\frac{3}{4}-i\frac{\sqrt{39}}{4}[/latex]
In this section we will practice simplifying and writing solutions to quadratic equations that are complex. We will then present a technique for classifying whether the solution(s) to a quadratic equation will be complex, and how many solutions there will be.
In our first example, we will work through the process of solving a quadratic equation with complex solutions. Take note that we will be simplifying complex numbers, so if you need a review of how to rewrite the square root of a negative number as an imaginary number, now is a good time.
Example
Use the Quadratic Formula to solve the equation [latex]x^{2}+2x=-5[/latex].
We can check these solutions in the original equation. Be careful when you expand the squares, and replace [latex]i^{2}[/latex] with [latex]-1[/latex].
| [latex]\begin{array}{r}x=-1+2i\\x^{2}+2x=-5\\\left(-1+2i\right)^{2}+2\left(-1+2i\right)=-5\\1-4i+4i^{2}-2+4i=-5\\1-4i+4\left(-1\right)-2+4i=-5\\1-4-2=-5\\-5=-5\end{array}[/latex] | [latex]\begin{array}{r}x=-1-2i\\x^{2}+2x=-5\\\left(-1-2i\right)^{2}+2\left(-1-2i\right)=-5\\1+4i+4i^{2}-2-4i=-5\\1+4i+4\left(-1\right)-2-4i=-5\\1-4-2=-5\\-5=-5\end{array}[/latex] |
Example
Use the quadratic formula to solve [latex]{x}^{2}+x+2=0[/latex].
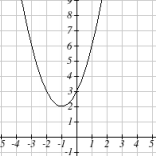
Now that we have had a little practice solving quadratic equations whose solutions are complex, we can explore a related feature of quadratic functions. Consider the following function: [latex]f(x)=x^2+2x+3[/latex]. Recall that the x-intercepts of a function are found by setting the function equal to zero:
[latex]x^2+2x+3=0[/latex]
The function now looks like the type of quadratic equations we have been solving. In the next example, we will solve this equation, then graph the original function and see that it has no x-intercepts.
Example
Find the x-intercepts of the quadratic function. [latex]f(x)=x^2+2x+3[/latex]
The following video gives another example of how to use the quadratic formula to find solutions to a quadratic equation that has complex solutions.
Summary
Quadratic equations can have complex solutions. Quadratic functions whose graphs do not cross the x-axis will have complex solutions for [latex]f(x)=0[/latex].
Applying the Quadratic Formula
Quadratic equations are widely used in science, business, and engineering. Quadratic equations are commonly used in situations where two things are multiplied together and they both depend on the same variable. For example, when working with area, if both dimensions are written in terms of the same variable, you use a quadratic equation. Because the quantity of a product sold often depends on the price, you sometimes use a quadratic equation to represent revenue as a product of the price and the quantity sold. Quadratic equations are also used when gravity is involved, such as the path of a ball or the shape of cables in a suspension bridge.
A very common and easy-to-understand application is the height of a ball thrown at the ground off a building. Because gravity will make the ball speed up as it falls, a quadratic equation can be used to estimate its height any time before it hits the ground. Note: The equation is not completely accurate, because friction from the air will slow the ball down a little. For our purposes, this is close enough.
Example
A ball is thrown off a building from [latex]200[/latex] feet above the ground. Its starting velocity (also called initial velocity) is [latex]−10[/latex] feet per second. The negative value means it is heading toward the ground.
The equation [latex]h=-16t^{2}-10t+200[/latex] can be used to model the height of the ball after t seconds. About how long does it take for the ball to hit the ground?
In the next video, we show another example of how the quadratic equation can be used to find the time it takes for an object in free fall to hit the ground.
The area problem below does not look like it includes a Quadratic Formula of any type, and the problem seems to be something you have solved many times before by simply multiplying. But in order to solve it, you will need to use a quadratic equation.
Example
Bob made a quilt that is [latex]4[/latex] ft [latex]\times[/latex] [latex]5[/latex] ft. He has [latex]10[/latex] sq. ft. of fabric he can use to add a border around the quilt. How wide should he make the border to use all the fabric? (The border must be the same width on all four sides.)
Our last video gives another example of using the quadratic formula for a geometry problem involving the border around a quilt.
Summary
Quadratic equations can appear in different applications. The Quadratic Formula is a useful way to solve these equations or any other quadratic equation! The Quadratic Formula, [latex]x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}[/latex], is found by completing the square of the quadratic equation [latex][/latex]. When you simplify using the quadratic formula and your result is a negative number under a square root, there are no real number solutions to the equation.
Learning Outcomes
- Use the quadratic formula to solve quadratic equations with complex solutions
- Connect complex solutions with the graph of a quadratic function that does not cross the x-axis
We have seen two outcomes for solutions to quadratic equations; either there was one or two real number solutions. We have also learned that it is possible to take the square root of a negative number by using imaginary numbers. Having this new knowledge allows us to explore one more possible outcome when we solve quadratic equations. Consider this equation:
[latex]2x^2+3x+6=0[/latex]
Using the Quadratic Formula to solve this equation, we first identify a, b, and c.
[latex]a = 2,b = 3,c = 6[/latex]
We can place a, b and c into the quadratic formula and simplify to get the following result:
[latex]x=-\frac{3}{4}+\frac{\sqrt{-39}}{4}, x=-\frac{3}{4}-\frac{\sqrt{-39}}{4}[/latex]
Up to this point, we would have said that [latex]\sqrt{-39}[/latex] is not defined for real numbers and determine that this equation has no solutions. But, now that we have defined the square root of a negative number, we can also define a solution to this equation as follows.
[latex]x=-\frac{3}{4}+i\frac{\sqrt{39}}{4}, x=-\frac{3}{4}-i\frac{\sqrt{39}}{4}[/latex]
In this section we will practice simplifying and writing solutions to quadratic equations that are complex. We will then present a technique for classifying whether the solution(s) to a quadratic equation will be complex, and how many solutions there will be.
In our first example, we will work through the process of solving a quadratic equation with complex solutions. Take note that we will be simplifying complex numbers, so if you need a review of how to rewrite the square root of a negative number as an imaginary number, now is a good time.
Example
Use the Quadratic Formula to solve the equation [latex]x^{2}+2x=-5[/latex].
We can check these solutions in the original equation. Be careful when you expand the squares, and replace [latex]i^{2}[/latex] with [latex]-1[/latex].
| [latex]\begin{array}{r}x=-1+2i\\x^{2}+2x=-5\\\left(-1+2i\right)^{2}+2\left(-1+2i\right)=-5\\1-4i+4i^{2}-2+4i=-5\\1-4i+4\left(-1\right)-2+4i=-5\\1-4-2=-5\\-5=-5\end{array}[/latex] | [latex]\begin{array}{r}x=-1-2i\\x^{2}+2x=-5\\\left(-1-2i\right)^{2}+2\left(-1-2i\right)=-5\\1+4i+4i^{2}-2-4i=-5\\1+4i+4\left(-1\right)-2-4i=-5\\1-4-2=-5\\-5=-5\end{array}[/latex] |
Example
Use the quadratic formula to solve [latex]{x}^{2}+x+2=0[/latex].
Now that we have had a little practice solving quadratic equations whose solutions are complex, we can explore a related feature of quadratic functions. Consider the following function: [latex]f(x)=x^2+2x+3[/latex]. Recall that the x-intercepts of a function are found by setting the function equal to zero:
[latex]x^2+2x+3=0[/latex]
The function now looks like the type of quadratic equations we have been solving. In the next example, we will solve this equation, then graph the original function and see that it has no x-intercepts.
Example
Find the x-intercepts of the quadratic function. [latex]f(x)=x^2+2x+3[/latex]
The following video gives another example of how to use the quadratic formula to find solutions to a quadratic equation that has complex solutions.
Summary
Quadratic equations can have complex solutions. Quadratic functions whose graphs do not cross the x-axis will have complex solutions for [latex]f(x)=0[/latex].
Candela Citations
- Quadratic Formula Application - Time for an Object to Hit the Ground. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/RcVeuJhcuL0. License: CC BY: Attribution
- Quadratic Formula Application - Determine the Width of a Border. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/Zxe-SdwutxA. License: CC BY: Attribution
- Ex2: Quadratic Formula - Two Real Irrational Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/tF0muV86dr0. License: CC BY: Attribution
- Ex: Quadratic Formula - Two Real Rational Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/xtwO-n8lRPw. License: CC BY: Attribution