Learning Outcomes
- Solve logarithmic equations using the definition of logarithms or 1-1 property.
The One-to-One Property of Logarithms
Some logarithmic equations can be solved in the same manner as the exponential equations in the previous section. Since the logarithm function also has the one-to-one property (its inverse is the exponential function), if two logarithms with common bases are set equal then their arguments must be equal as well.
ONE-TO-ONE PROPERTY OF LOGARITHMS
Let [latex]b>0[/latex] and [latex]b \neq 1.[/latex] Then [latex]\log_b(x) = \log_b(y)[/latex] implies [latex]x=y.[/latex]
This also applies when the arguments are algebraic expressions.
For example, if [latex]\log_2(x-1)=\log_2(8),\text{then }x-1=8[/latex] and [latex]x=9.[/latex] To check, we can substitute [latex]x=9[/latex] into the original equation: [latex]{\mathrm{log}}_{2}\left(9 - 1\right)={\mathrm{log}}_{2}\left(8\right)=3[/latex].
![]() Make sure to always check your answer! The logarithm function has domain [latex](0,\infty)[/latex] so any solutions must result in all logarithms having positive arguments. A solution that results in an argument that is zero or negative in a logarithm is an extraneous solution.
Make sure to always check your answer! The logarithm function has domain [latex](0,\infty)[/latex] so any solutions must result in all logarithms having positive arguments. A solution that results in an argument that is zero or negative in a logarithm is an extraneous solution.
Try the following example to test your understanding so far.
Example
Solve [latex]\log(3x - 2)=\log(x+4)[/latex]. Check your solutions.
Here is another example with more complicated arguments. Note that in the context of these examples, the base of the logarithm does not matter as long as it is the same base on both sides.
Example
Solve [latex]\ln(x^2-3)=\ln(2x)[/latex].
Using the Definition of a Logarithm
We have already seen that every logarithmic equation [latex]\log_b(x)=y[/latex] can be written as the exponential equation [latex]b^y=x[/latex]. We can use this fact to solve logarithmic equations where the argument is an algebraic expression.
For example, consider the equation [latex]\log_2(6x - 10)=3[/latex]. To solve this equation, we can apply the definition of logarithms which puts the expression containing [latex]x[/latex] by itself on one side of the equation:
[latex]\begin{align}\log_2(6x - 10)&=3 \\ 2^3&=6x-10 && \color{blue}{\textsf{rewrite using the definition of logarithms}} \\ 8&=6x-10\\ 18&=6x\\ 3&=x \end{align}[/latex]
Example
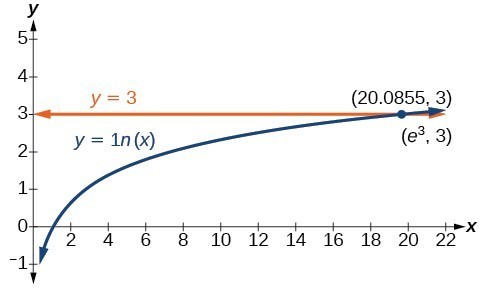
Solve [latex]\ln(x)=3[/latex].
In the same way that a story can help you understand a complex concept, graphs can help us understand a wide variety of concepts in mathematics. Visual representations of the parts of an equation can be created by turning each side into a function and plotting the functions on the same set of axes.
Example
Solve [latex]2\ln(x+3)=7[/latex]. Write your final answer both in exact form and approximated to two decimal places.
Summary
The One-to-One Property of Logarithms can solve logarithmic equations where both sides of the equation have a logarithm with the same base. If there is only a single logarithm, we can use the definition of a logarithm to rewrite the equation as an exponential equation.
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175. License: CC BY: Attribution. License Terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175.