Learning Objectives
- Solve applications of systems of two linear equations with two variables using substitution or elimination.
In this section we present examples of applications which are solved using systems of linear equations.
If you need a refresher on how to solve systems of linear equations by substitution and elimination, first visit Section 2.R: Solving Linear Systems of Equations by Substitution and Elimination.
Cost, Revenue, and Profit
A skateboard manufacturer introduces a new line of boards. The manufacturer tracks its costs, which is the amount it spends to produce the boards, and its revenue, which is the amount it earns through sales of its boards. How can the company determine if it is making a profit with its new line? How many skateboards must be produced and sold before a profit is possible?

(credit: Thomas Sørenes)
The skateboard manufacturer’s revenue function is the function used to calculate the amount of money that comes into the business. It can be represented by the equation [latex]R=xp[/latex], where [latex]x=[/latex] quantity and [latex]p=[/latex] price per unit. The revenue function is shown in orange in the graph below.
The cost function is the function used to calculate the total cost of doing business. It includes fixed costs, such as rent and salaries, and variable costs, such as utilities. The cost function is shown in blue in the graph below. The [latex]x[/latex]-axis represents quantity in hundreds of units. The [latex]y[/latex]-axis represents either cost or revenue in hundreds of dollars.
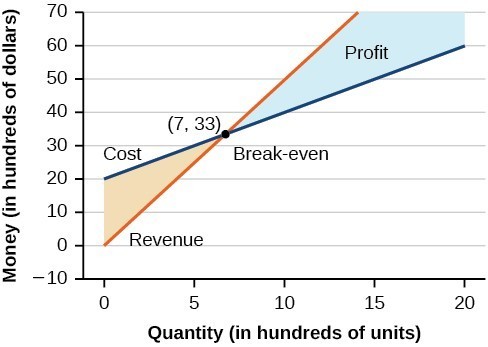
The point at which the two lines intersect is called the break-even point. We can see from the graph that if [latex]700[/latex] units are produced, the cost is [latex]\$3,300[/latex] and the revenue is also [latex]\$3,300[/latex]. In other words, the company breaks even if they produce and sell [latex]700[/latex] units. They neither make money nor lose money.
The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss. The profit function is the revenue function minus the cost function, written as [latex]P\left(x\right)=R\left(x\right)-C\left(x\right)[/latex]. Note that when [latex]R(x)=C(x),[/latex] then [latex]P(x)=0.[/latex] Clearly, knowing the quantity for which the cost equals the revenue is of great importance to businesses.
Example
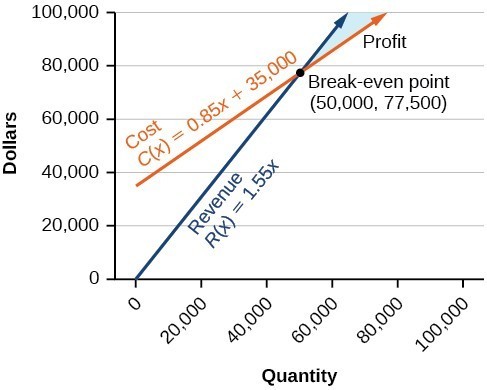
A business wants to manufacture bike frames. Before they start production, they need to make sure they can make a profit with the materials and labor force they have. Their accountant has given them a cost equation of [latex]y=0.85x+35,000[/latex] and a revenue equation of [latex]y=1.55x.[/latex]
- Interpret [latex]x[/latex] and [latex]y[/latex] for the cost equation.
- Interpret [latex]x[/latex] and [latex]y[/latex] for the revenue equation.
- Find and interpret the break-even point for this business.
Total Value Problems
In the next set of examples, we are given two types of items and multiple descriptions of their “value.” For example, we may be given two types of tickets sold at a circus and the totals of number of tickets sold as well as the total sales (or revenue).
Example
The cost of a ticket to the circus is [latex]\$25.00[/latex] for children and [latex]\$50.00[/latex] for adults. On a certain day, attendance at the circus is [latex]2,000[/latex] and the total gate revenue is [latex]\$70,000[/latex]. How many children and how many adults bought tickets?
In this video example we show how to set up a system of linear equations that represents the total cost for admission to a museum.
Try It YOURSELF
Mixture Problems
A solution is a mixture of two or more different substances like water and salt or vinegar and oil. Mixture problems are ones where two different solutions are mixed together resulting in a new final solution. Most biochemical reactions occur in liquid solutions, making them important for doctors, nurses, and researchers to understand.
The concentration or strength of a liquid solution is often described as a percentage. This number comes from the ratio of how much mass is in a specific volume of liquid. For example if you have [latex]50[/latex] grams of salt in a [latex]100[/latex] mL of water you have a [latex]50\%[/latex] salt solution based on the following ratio:
[latex]\frac{50\text{ grams }}{100\text{ mL }}=0.50\frac{\text{ grams }}{\text{ mL }}=50\text{ % }\frac{\text{ grams }}{\text{ mL }}[/latex]
Solutions used for most purposes typically come in pre-made concentrations from manufacturers, so if you need a custom concentration, you would need to mix two different strengths. For example, you may have a [latex]9\%[/latex] solution and a [latex]20\%[/latex] solution on hand, and need to mix them to create a [latex]16\%[/latex] solution.
We will use the following table to help us solve mixture problems. The units on the last row will change from problem to problem based on what the concentration is describing. In the above example, the last row would represent grams of salt.
| Solution 1 | Solution 2 | Totals | |
| Amount | |||
| Concentration | |||
| Value |
Consider mixing the following two solutions together:
- One is [latex]120[/latex] mL of a [latex]9\%\dfrac{\text{grams}}{\text{mL}}[/latex] solution,
- The other is [latex]75[/latex] mL of a [latex]23\%\dfrac{\text{grams}}{\text{mL}}[/latex] solution.
Let’s determine the concentration of the resulting solution using our table. First we place the values we know into the table. Note that while the concentrations are usually given to you as percentages, we will use their decimal form when performing computations.
| Solution 1 | Solution 2 | Totals | |
| Amount | [latex]120[/latex] mL | [latex]75[/latex] mL | |
| Concentration | [latex]0.09\dfrac{\text{ grams }}{\text{ mL }}[/latex] | [latex]0.23\dfrac{\text{ grams }}{\text{ mL }}[/latex] | |
| Value |
Now fill in the values in the bottom row by multiplying amount by concentration in each column.
| Solution 1 | Solution 2 | Totals | |
| Amount | [latex]\require{color}120[/latex] mL | [latex]75[/latex] mL | |
| Concentration | [latex]0.09\dfrac{\text{ grams }}{\text{ mL }}[/latex] | [latex]0.23\dfrac{\text{ grams }}{\text{ mL }}[/latex] | |
| Value | [latex]\left(120{\color{red}\cancel{\color{black}{\text{ mL}}}}\right)\left(0.09\dfrac{\text{ grams }}{{\color{red}\cancel{\color{black}{\text{ mL }}}}}\right)=10.8\text{ grams }[/latex] | [latex]\left(75\color{red}\cancel{\color{black}{\text{ mL}}}\right)\left(0.23\dfrac{\text{ grams }}{\color{red}\cancel{\color{black}{\text{ mL }}}}\right)=17.25\text{ grams }[/latex] |
Finally, complete the Totals column. Our final answer is the total of the Concentration row, found by dividing totals of Value and Amount.
| Solution 1 | Solution 2 | Totals | |
| Amount | [latex]120[/latex] mL | [latex]75[/latex] mL | [latex]195[/latex] mL |
| Concentration | [latex]0.09\dfrac{\text{ grams }}{\text{ mL }}[/latex] | [latex]0.23\dfrac{\text{ grams }}{\text{ mL }}[/latex] | [latex]\frac{28.05\text{ grams }}{ 195 \text{ mL }}\approx0.14=14\text{ % }[/latex] |
| Value | [latex]10.8 \text{ grams }[/latex] | [latex]17.25 \text{ grams }[/latex] | [latex]10.8\text{ grams }+17.25\text{ grams }=28.05\text{ grams }[/latex] |
The final solution has a concentration of about [latex]14\%\dfrac{\text{ grams }}{\text{ mL }}[/latex]. If the context of this concentration is clear or the units are not clearly specified, we will often just say the concentration is [latex]14\%[/latex] without specifying units.
In the following examples, you will see that we can use the table to find an unknown final volume or concentration. These problems can have either one or two variables. We will start with one variable problems, then move to two variable problems.
Example
A chemist has [latex]70[/latex] mL of a [latex]50\%[/latex] methane solution. How much of an [latex]80\%[/latex] solution must she add so the final solution is [latex]60\%[/latex] methane?
The above problem illustrates how we can use the mixture table to define an equation to solve for an unknown volume. In the next example we will start with two known concentrations and use a system of equations to find two starting volumes necessary to achieve a specified final concentration.
Example
A farmer has two types of milk, one that is [latex]24\%[/latex] butterfat and another that is [latex]18\%[/latex] butterfat. How much of each should he use to end up with [latex]42[/latex] gallons of [latex]20\%[/latex] butterfat?
In the following video you will be given an example of how to solve a mixture problem without using a table, and interpret the results.
In the preceding mixture problems, our equations involved a concentration which had the form of a rate (which we wrote as a percent). Here is one more example that uses a different kind of rate.
EXAMPLE
A store owner wants to develop a new snack mix by mixing cashews and raisins. The cashews cost [latex]\$6.50[/latex] per pound and the raisins cost [latex]\$4.00[/latex] per pound. How much of each should be used to obtain [latex]40[/latex] pounds of snack mix worth [latex]\$4.75[/latex] per pound?
Motion Problems
In this section we will work with uniform motion, or motion with a constant speed. Uniform motion can be modeled by the following equation:
UNIFORM MOTION
If an object in uniform motion has speed [latex]r[/latex] and travels for amount of time [latex]t[/latex], the distance [latex]d[/latex] that it travels is given by
[latex]d = r \cdot t.[/latex]
Here is an example of a motion problem with two unknowns to solve for. Each object in motion results in a separate instance of the uniform motion equation.
EXAMPLE
A train leaves a station traveling north at [latex]56[/latex] km/hr. A second train leaves [latex]4[/latex] hours later traveling north on a parallel track at [latex]84[/latex] km/hr. How far from the station will the second train pass the first train?
Many real-world applications of uniform motion arise because of the effects of currents—of water or air—on the actual speed of a vehicle. Cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.
Let’s take a look at a boat travelling on a river. Depending on which way the boat is going, the current of the water is either slowing it down or speeding it up.
The images below show how a river current affects the speed at which a boat is actually travelling. We’ll call the speed of the boat in still water [latex]b[/latex] and the speed of the river current [latex]c[/latex].
The boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat’s actual speed is faster than its speed in still water. The actual speed at which the boat is moving is [latex]b+c[/latex].
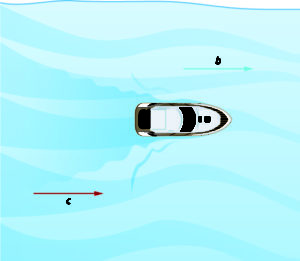
Now, the boat is going upstream, opposite to the river current. The current is going against the boat, so the boat’s actual speed is slower than its speed in still water. The actual speed of the boat is [latex]b-c[/latex]. In examples, sometimes one or both of [latex]b[/latex] and [latex]c[/latex] is given to you. It is important that [latex]b[/latex] is always first when subtracting.
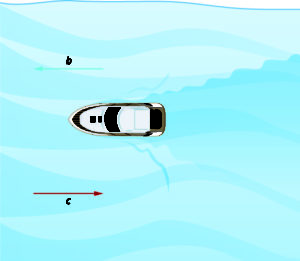
We’ll put some numbers to this situation in the next example.
EXAMPLE
Translate to a system of equations and then solve.
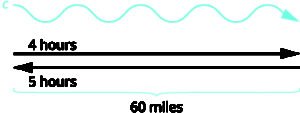
A river cruise ship sailed [latex]60[/latex] miles downstream for [latex]4[/latex] hours and then took [latex]5[/latex] hours sailing upstream to return to the dock. Find the speed of the ship in still water and the speed of the river current.
In the next video, we present another example of a uniform motion problem which can be solved with a system of linear equations.
Depending on the information given in the problem, there are many different setups with which you can start a motion problem. Focus on using the table with Distance = Rate [latex]\cdot[/latex] Time, filling in any known quantities and representing unknown quantities by variables. Make sure if you know any relationships between unknown quantities, you use as few total variables as possible. Also make sure you represent Rate by two components if necessary (for example, boat speed and current with boat speed first).
Summary
Systems of equations in two variables are useful for solving a variety of application problems. They can find break-even points in business applications, solve total value problems and mixture problems, and solve for unknowns in problems of motion. Often a chart or table can be useful to organize information that is known or unknown, and also to set up the equations.
Candela Citations
- Precalculus. Authored by: OpenStax College . Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution
- Revision and Adaptation. Authored by: Lumen Learning. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Solving Systems of Equations using Elimination. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/ova8GSmPV4o. License: CC BY: Attribution
- Question ID 115164, 115120, 115110. Authored by: Shabazian, Roy. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Beginning and Intermediate Algebra. Authored by: Wallace, Tyler. Located at: http://www.wallace.ccfaculty.org/book/book.html. License: CC BY: Attribution
- Question ID 29699. Authored by: McClure, Caren. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 23774. Authored by: Shahbazian, Roy. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 8589. Authored by: Greg Harbaugh. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 2239. Authored by: Morales, Lawrence. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Ex: System of Equations Application - Mixture Problem.. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning.. Located at: https://youtu.be/4s5MCqphpKo.. License: CC BY: Attribution
- Beginning and Intermediate Algebra Textbook. . Authored by: Tyler Wallace. Located at: http://www.wallace.ccfaculty.org/book/book.html.%20. License: CC BY: Attribution
- Ex: System of Equations Application - Plane and Wind problem. Authored by: James Sousa (Mathispower4u.com). Located at: https://www.youtube.com/watch?v=OuxMYTqDhxw. License: CC BY: Attribution
- Intermediate Algebra . Authored by: Lynn Marecek et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13