Learning OutcomeS
- Determine whether an ordered pair is a solution of a two-variable linear inequality.
- Graph the solution set of a single two-variable linear inequality.
- Graph the solution set of a system of two-variable linear inequalities with two inequalities.
- Graph the solution set of a system of two-variable linear inequalities with more than two inequalities.
A linear inequality is the same as a linear equation [latex]Ax+By=C,[/latex] but with the equal sign replaced with an inequality sign. An example is [latex]2x-3y\leq4.[/latex] Often a linear inequality is written in “slope-intercept form,” for example [latex]y\leq x-2.[/latex]
An ordered pair is a solution if it makes the inequality true when we substitute [latex]x[/latex] and [latex]y.[/latex] Here is a quick example.
ExAMPLE
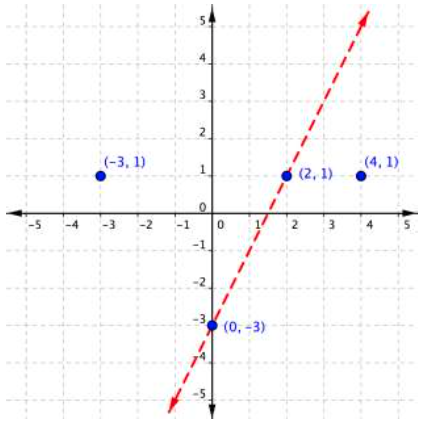
Determine whether each ordered pair is a solution to the inequality [latex]y>x+4.[/latex]
- [latex](0,0)[/latex]
- [latex](1,6)[/latex]
It is not a useful strategy to find all solutions to a linear inequality by testing single ordered pairs. We will see that linear inequalities have infinitely many solutions, so a graph in the coordinate plane is a good way to represent the solution set.
Let’s consider a first example, to graph the inequality
[latex]x+4y\leq4[/latex].
Any point on the line [latex]x+4y=4[/latex] will satisfy the inequality since this inequality symbol allows equality, so we begin by graphing the line. You can use the [latex]x[/latex] and [latex]y[/latex]-intercepts for this equation to graph the line. For example, find the [latex]y[/latex]-intercept by setting [latex]x=0[/latex] and solving for [latex]y.[/latex]
| [latex]x[/latex] | [latex]y[/latex] |
| [latex]0[/latex] | [latex]1[/latex] |
| [latex]4[/latex] | [latex]0[/latex] |
Plot the points [latex](0,1)[/latex] and [latex](4,0)[/latex], and draw a line through these two points. This line is called the boundary line.
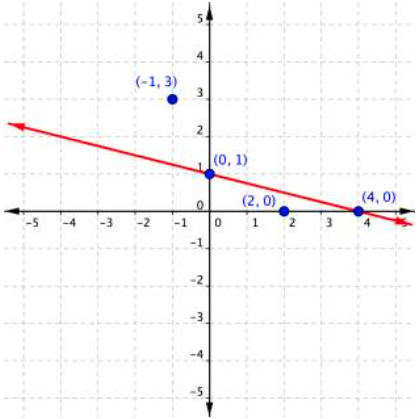
Next, let’s test a couple of ordered pairs, one on each side of the boundary line.
If you substitute [latex](−1,3)[/latex] into [latex]x+4y\leq4[/latex]:
[latex]\begin{array}{r}−1+4\left(3\right)\overset{?}{\leq}4\\−1+12\overset{?}{\leq}4\\11\not\leq4\end{array}[/latex]
This is a false statement so [latex](−1,3)[/latex] is not a solution.
On the other hand, if you substitute [latex](2,0)[/latex] into [latex]x+4y\leq4[/latex]:
[latex]\begin{array}{r}2+4\left(0\right)\overset{?}{\leq}4\\2+0\overset{?}{\leq}4\\2\leq4\end{array}[/latex]
This is true! As it turns out, the boundary line is the dividing line between solutions and non-solutions. We call each side of the line a half-plane. The half-plane that includes [latex](2,0)[/latex] should be shaded to indicate this is the region of solutions for the inequality. The half-plane that includes [latex](-1,3)[/latex] has no solutions.
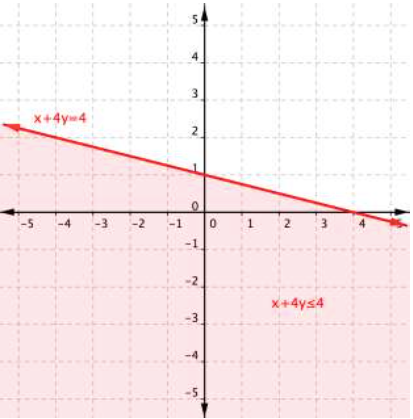
And there you have it, the graph of the set of solutions for [latex]x+4y\leq4[/latex]. Here is our process in summarized form.
Graphing a linear inequality
- Graph the related boundary line. Replace the <, >, ≤ or ≥ sign in the inequality with = to find the equation of the boundary line.
- If points on the boundary line are solutions, then use a solid line for drawing the boundary line. This will happen for ≤ or ≥ inequalities.
- If points on the boundary line are not solutions, then use a dashed line for the boundary line. This will happen for < or > inequalities.
- Identify at least one ordered pair on either side of the boundary line and substitute those [latex](x,y)[/latex] values into the inequality. Shade the half-plane that contains the ordered pairs that make the inequality a true statement.
Below is a video about how to graph inequalities with two variables.
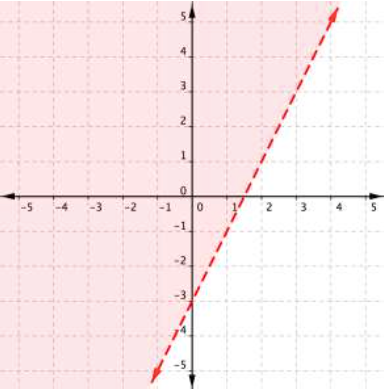
Example
Graph the inequality [latex]2y>4x–6[/latex].
If you rewrite your inequality in slope-intercept form as in the previous example, it provides an alternative approach to deciding the direction of shading. A [latex]>[/latex] or [latex]\geq[/latex] symbol as we had in that example always means shade above the line. A [latex]<[/latex] or [latex]\leq[/latex] symbol means shade below. Note this approach does not work unless the inequality is put into slope-intercept form!
This video gives an example of using this alternative approach to do the shading.
Systems of Two or More Inequalities
The graph of a single linear inequality in two variables splits the coordinate plane into two regions. On one side lie all the solutions to the inequality. Now consider the system of inequalities,
[latex]\left\{ \begin{array}{l}y<2x+5\\y>-x \end{array} \right.[/latex]
Here are the graphs of each inequality independently.
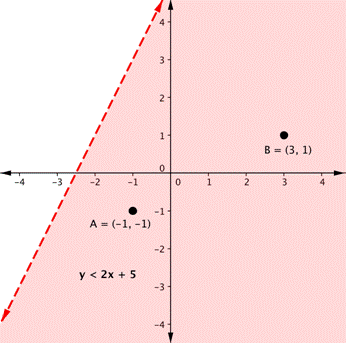
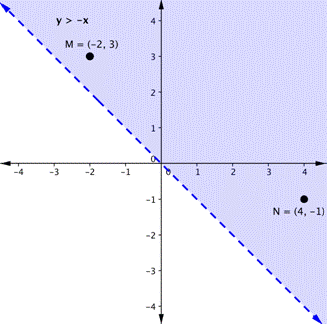
You can verify by substitution that points [latex]A[/latex] and [latex]B[/latex] satisfy the first inequality, while points [latex]M[/latex] and [latex]N[/latex] satisfy the second inequality.
A solution to a system of inequalities must satisfy both inequalities at the same time. The solution set consists of all points which satisfy both inequalities. The easiest way to find the solution set is to graph both inequalities on the same graph and find the region of overlap.
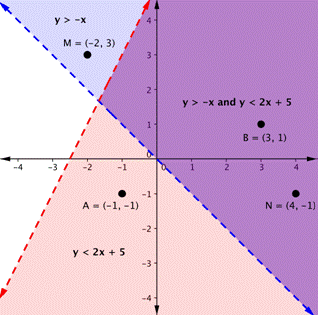
The purple area shows where the solutions of the two inequalities overlap. This area is the solution to the system of inequalities. Any point within this purple region will be true for both [latex]y<2x+5[/latex] and [latex]y>−x.[/latex] Note in particular that the blue and red regions do NOT solve the system because they only satisfy one of the two inequalities. In the future, we will usually only shade the overlap region to avoid confusion.
We can verify by substitution that the point [latex]M=(-2,3)[/latex] in the blue region is not a solution to the system since it does not satisfy the first inequality:
[latex]\begin{align}y&<2x+5\\ 3&<2(-2)+5\\ 3&<-4+5\\ 3&<1&&\color{red}{\textsf{False}}\end{align}[/latex]
In the following video examples, we show how to graph a system of linear inequalities and define the solution region.
The general steps are outlined below.
Graphing a SYSTEm of linear inequalities
- Graph all inequalities on the same axes. Determine whether each line is solid or dashed and which side of each line to shade on.
- Shade the region that represents the overlap of all solution regions for inequalities in the system.
The system in our next example includes a compound inequality. We will see that you can treat a compound inequality like two inequalities when you are graphing them, so this example is basically a system of three inequalities.
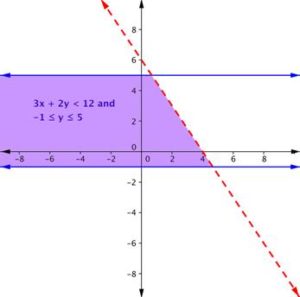
Example
Graph the system
[latex]\left\{ \begin{array}{rl}3x+2y&<12\\-1 \leq y &\leq 5 \end{array} \right.[/latex]
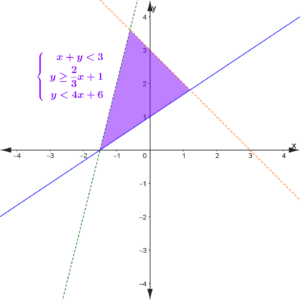
The next example is explicitly a system of three inequalities to graph.
EXAMPLE
Graph the system
[latex]\left\{ \begin{array}{rl}x+y<3\\y\geq\dfrac{2}{3}x+1\\y<4x+6 \end{array} \right.[/latex]
Summary
When linear inequalities are graphed on a coordinate plane, the solution takes the form of all points on one side of the boundary line, and possibly also the line itself. You can tell which region to shade by testing some points in the inequality, or observing the direction of the sign if the inequality is in slope-intercept form. When graphing a system of linear inequalities, graph all inequalities on the same axes. The solution set is the overlap of all the individual solution sets.
Candela Citations
- Ex 1: Graphing Linear Inequalities in Two Variables (Slope Intercept Form). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/Hzxc4HASygU. License: CC BY: Attribution
- Ex 2: Graphing Linear Inequalities in Two Variables (Standard Form). Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/2VgFg2ztspI. License: CC BY: Attribution
- Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution