To Learning Outcomes
- Determine if a graph is the graph of a function by using the Vertical Line Test.
- Find the value of a function from a graph.
- State the domain and range from the graph of a function in set-builder, inequality, and/or interval notation.
- Evaluate functions at a given input value using an equation. Also, determine inputs resulting in the given output value
- Using the equation of a function, state the domain in set-builder, inequality, and/or interval notation.
Functions
You should be familiar with functions from previous math courses. Here, we’ll do a quick review. Some people think of functions as “mathematical machines.” Imagine you have a machine that changes a number according to a specific rule such as “multiply by [latex]3[/latex] and add [latex]2[/latex]” or “divide by [latex]5[/latex], add [latex]25[/latex], and multiply by [latex]−1[/latex].” If you put a number into the machine, a new number will come out the other end having been changed according to the rule. The number that goes in is called the input, and the number that is produced is called the output.
You can also call the machine “[latex]f[/latex]” for function. If you put [latex]x[/latex] into the machine, [latex]f(x)[/latex] (read “[latex]f[/latex] of [latex]x[/latex]“), comes out. Mathematically speaking, [latex]x[/latex] is the input, or the independent variable, and [latex]f(x)[/latex] is the output, or the dependent variable, since it depends on the value of [latex]x[/latex].
Relations and Functions
In mathematics, a relation is a set of ordered pairs. The set of first components of the ordered pairs is called the domain and the set of second components of the ordered pairs is called the range. In a set of ordered pairs, you find the domain by listing all of the input values (the [latex]x[/latex]-coordinates). To find the range, list all of the output values (the [latex]y[/latex]-coordinates).
A function is a special type of relation in which each domain value corresponds to exactly one range value.
If you find that you need more help understanding functions, please click on the link to learn more about functions.
Consider the following relation: [latex]\{(−2,0),(0,6),(-2,12),(4,18)\}[/latex].
For this relation, the domain is [latex]\{−2,0,4\}[/latex] and the range is [latex]\{0,6,12,18\}[/latex].
Is the above relation a function or not?
This relation is NOT a function because the input values are not unique, in other words, there is a repeated [latex]x[/latex]-value that corresponds to different [latex]y[/latex]-values.
Example
List the domain and range for the following relation where [latex]x[/latex] is the input and [latex]f(x)[/latex] is the output and determine whether the relation given is a function. Remember each pair of [latex]x[/latex] and [latex]f(x)[/latex] exists as a point [latex](x,f(x))[/latex] on the graph of the function .
| [latex]x[/latex] | [latex]f(x)[/latex] |
|---|---|
| [latex]−3[/latex] | [latex]4[/latex] |
| [latex]−2[/latex] | [latex]2[/latex] |
| [latex]−1[/latex] | [latex]1[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
| [latex]3[/latex] | [latex]4[/latex] |
In the following video we provide another example of identifying domain and range. Determine whether the table of values represents a function.
In the above video, each domain value corresponds to exactly one range value. No [latex]x[/latex]-coordinates were repeated so that relation is a function.
Function Notation
The notation [latex]y=f\left(x\right)[/latex] defines a function named [latex]f[/latex]. The letter [latex]x[/latex] represents the input value, or independent variable. The letter [latex]y[/latex] or [latex]f\left(x\right)[/latex], represents the output value, or dependent variable. When a function is defined by an equation, we usually use function notation.
For example, the equation [latex]y=3x+1[/latex] may also be written as [latex]f(x)=3x+1[/latex]. [latex]f[/latex] is the name of the function, [latex]x[/latex] is an input from the domain of the function, and [latex]f(x)[/latex] is the function value at [latex]x[/latex] also called the output.
Inputs of Functions
A function can be evaluated at different values of [latex]x[/latex]. Given the function [latex]f(x)=3x+1[/latex], find [latex]f(-2)[/latex]. In other words, if [latex]x[/latex] is [latex]-2[/latex] find [latex]f(x)[/latex]. We must substitute [latex]\color{Green}{-2}[/latex] in place of [latex]\color{Green}{x}[/latex] and evaluate.
[latex]\begin{align} f(\color{Green}{-2}\color{black}{)} &= 3(\color{Green}{-2}\color{black}{)+1}\\ &=-6+1\\ &= -5 \end{align}[/latex]
So, when [latex]x=-2[/latex], [latex]f(x)=-5[/latex] (or [latex]y=-5[/latex]). This can be written as the ordered pair [latex](-2,-5)[/latex] and it is a point on the graph of the line [latex]f(x)=3x+1[/latex].
It is important to note that the parentheses that are part of function notation do not mean multiply. The notation [latex]f(x)[/latex] does not mean [latex]f[/latex] multiplied by [latex]x[/latex]. Instead, the notation means “[latex]f\text{ of } x[/latex]” or “the function of [latex]x[/latex].” To evaluate the function, take the value given for [latex]x[/latex], and substitute that value in for [latex]x[/latex] in the expression.
Let us look at a couple of examples.
ExAMple
Given [latex]f(x)=3x–4[/latex], evaluate [latex]f(5)[/latex].
Example
Given [latex]p(x)=-2x^{2}+5[/latex], evaluate [latex]p(−3)[/latex].
Example
Given [latex]f(x)=|4x-3|[/latex], evaluate [latex]f(0)[/latex], [latex]f(2)[/latex], and [latex]f(−1)[/latex].
Outputs of Functions
Reconsider the equation [latex]y=4x+1[/latex], which represents a function. If instead of having a given input value, you have a known output value, you can find the input value that would give that output. For example, for an output value of [latex]-7[/latex], you can find the input value. First substitute [latex]\color{Green}{y=-7}[/latex] into the equation and then solve for [latex]x[/latex].
[latex]\begin{align}\color{Green}{y} &= 4x+1\\ \color{Green}{-7} &= 4x+1\\ -7-1 &= 4x\\ -8 &= 4x\\ \frac{-8}{4} &= x\\ -2 &= x\\ x &= -2\end{align}[/latex]
The output of [latex]-7[/latex] corresponds to an input of [latex]-2[/latex]. These values make an ordered pair, [latex](-2, -7)[/latex], that represents a point on the graph of this function. We will discuss this idea more fully later in this section.
In the next example, you will not be given the [latex]x[/latex]-value but instead you will be given a [latex]y[/latex]-value and asked to find the [latex]x[/latex]-value.
Example
Given [latex]f(x)=3x–4[/latex], find the [latex]x[/latex]-value that yields an output of [latex]5[/latex].
Try It
Graphs of Functions and the Vertical Line Test
When both the independent quantity (input) and the dependent quantity (output) are real numbers, a function can be represented by a graph in the coordinate plane. The independent value is plotted on the [latex]x[/latex]-axis and the dependent value is plotted on the [latex]y[/latex]-axis. The fact that each input value has exactly one output value means graphs of functions have certain characteristics. For each input on the graph, there will be exactly one output. For a function defined as [latex]y = f(x)[/latex], or “[latex]y[/latex] is a function of [latex]x[/latex]“, we would write ordered pairs [latex](x, f(x))[/latex] using function notation instead of [latex](x,y)[/latex] as you may have seen previously.
We can identify whether the graph of a relation represents a function because for each [latex]x[/latex]-coordinate there will be exactly one [latex]y[/latex]-coordinate. The blue relation graphed below represents a function. Notice that when a vertical line is placed over the graph, the line does not intersect the graph more than once for any value of [latex]x[/latex]. This indicates that the relation is a function.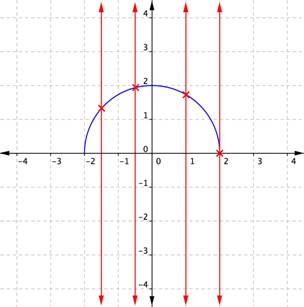 If instead a graph shows two or more intersections with a vertical line, then an input ([latex]x[/latex]-coordinate) has more than one output ([latex]y[/latex]-coordinate), and [latex]y[/latex] is not a function of [latex]x[/latex].
If instead a graph shows two or more intersections with a vertical line, then an input ([latex]x[/latex]-coordinate) has more than one output ([latex]y[/latex]-coordinate), and [latex]y[/latex] is not a function of [latex]x[/latex].
Examining the graph of a relation to determine if a vertical line would intersect with more than one point is a quick way to determine if the relation shown by the graph is a function. This method is often called the Vertical Line Test.
Example
Use the vertical line test to determine whether the relation plotted on this graph is a function.

Find the Value of a Function from a Graph
Example
A function is graphed below.
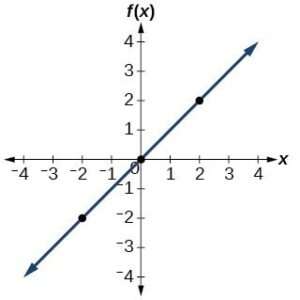
- For the given function, evaluate [latex]f(2)[/latex].
- For the given graph of a function, find [latex]x[/latex] when [latex]f(x)=-2[/latex].
ExAmple
A function is graphed below.
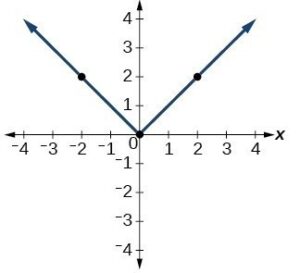
- For the given function, evaluate [latex]f(-1)[/latex].
- For the given function, evaluate [latex]f(0)[/latex].
- For the given graph of a function, find [latex]x[/latex] when [latex]f(x)=2[/latex].
Try It
Finding the Domain and Range of a Function from its Graph
Finding domain of different functions is often a matter of asking yourself, “what values of [latex]x[/latex] can this function not have?” Pictures make it easier to visualize what the domain and range are, so we will first show how to define the domain and range of functions given their graphs. What are the domain and range of the function [latex]f(x)=x+3[/latex]?
This is a linear function. Remember that linear functions are lines that continue forever in each direction.
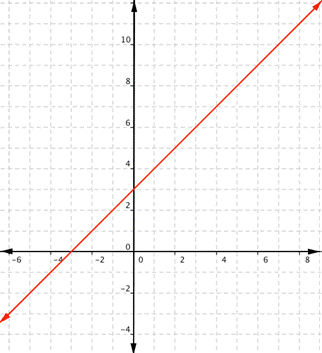
Graph of the function [latex]f(x)=x+3[/latex]
For this function, any real number can be substituted for [latex]x[/latex] and you will get a meaningful output. Also, for any real number, you can always find an [latex]x[/latex] value that gives you that number for the output. Unless a linear function is a constant, such as [latex]f(x)=2[/latex], there is no restriction on the range. For the function [latex]f(x)=x+3[/latex], the domain and range are all real numbers. We can write this domain and range in a variety of formats.
| Domain | Range | |
| Set-Builder Notation | [latex]\{x|\text{all real numbers}\}[/latex] | [latex]\{y|\text{all real numbers}\}[/latex] |
| Inequality Notation | [latex]-\infty| [latex]-\infty | |
| Interval Notation | [latex](-\infty,\infty)[/latex] | [latex](-\infty,\infty)[/latex] |
For the examples that follow, try to figure out the domain and range of the graphs before you look at the answer.
Example
Use the graph to determine the domain and range of the function [latex]f(x)=−3x^{2}+6x+1.[/latex]
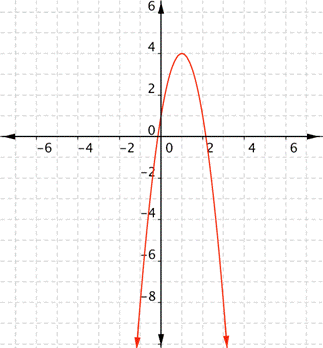
Exercises
Use the graph to determine the domain and range of the real-valued function [latex]f(x)=-2+\sqrt{x+5}.[/latex]
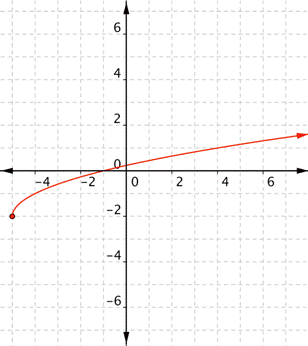
Try the following problem, remembering to look at the graph for the lowest and highest [latex]x[/latex]-values that appear in the graph to find the domain, then for the smallest and highest [latex]y[/latex]-values to find the range. Make sure to notice if the graph has arrows or endpoints. That will change how you write your answer.
Try It
In the following video we show how to define the domain and range of functions from their graphs.
Finding the Domain and Range from the Equation of a Function
For this discussion, we will restrict all functions to real number values for the domain and range. Even with this starting point, it does not mean that for any function we discuss that all real numbers can be used for [latex]x[/latex]. It also does not mean that all real numbers can be function output values, [latex]f(x)[/latex]. There may be restrictions on the domain and range. The restrictions partly depend on the type of function.
Domain restrictions
In our course, there are two main reasons why domains are restricted.
- You cannot divide by [latex]0[/latex].
If you have a function like [latex]f(x)=\frac{1}{x-2}[/latex], the domain has to be restricted so that no inputs make the denominator zero. For this example, [latex]x[/latex] cannot be [latex]2[/latex] because if you replace [latex]x[/latex] with [latex]2[/latex], you will end up with the denominator as zero which is undefined. The domain would be [latex](-\infty,2)\cup(2,\infty)[/latex]. - You cannot take the square (or other even) root of a negative number, as the result will not be a real number.
If you have a function like [latex]f(x)=\sqrt{x}[/latex], the domain has to be restricted so that we don’t take the square root of a negative number. Recall that the number or expression written under a root symbol is called the radicand. The radicand of a square (or other even) root must not be negative. Then the domain for this example would be [latex]x\ge0[/latex] or [latex][0,\infty)[/latex].
Example
State the domain of the function [latex]f(x)=\dfrac{x+1}{x-3}[/latex].
Example
State the domain of the function [latex]f(x)=\sqrt{2x+1}[/latex].
In the following video, only watch the first example given. We will talk about the other two examples later in the course.
Try It
State the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex 1: Find Domain and Range of Ordered Pairs, Function or Not. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/kzgLfwgxE8g. License: CC BY: Attribution
- College Algebra. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface.%20. License: CC BY: Attribution
- Ex: Give the Domain and Range Given the Points in a Table. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/GPBq18fCEv4. License: CC BY: Attribution
- Ex: Determine if a Table of Values Represents a Function. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/y2TqnP_6M1s. License: CC BY: Attribution

