A skateboard manufacturer introduces a new line of boards. The manufacturer tracks its costs, which is the amount it spends to produce the boards, and its revenue, which is the amount it earns through sales of its boards. How can the company determine if it is making a profit with its new line? How many skateboards must be produced and sold before a profit is possible?
(credit: Thomas Sørenes)
The skateboard manufacturer’s revenue function is the function used to calculate the amount of money that comes into the business. It can be represented by the equation [latex]R=xp[/latex], where [latex]x=[/latex] quantity and [latex]p=[/latex] price per unit. The revenue function is shown in orange in the graph below.
The cost function is the function used to calculate the total cost of doing business. It includes fixed costs, such as rent and salaries, and variable costs, such as utilities. The cost function is shown in blue in the graph below. The [latex]x[/latex]-axis represents quantity in hundreds of units. The [latex]y[/latex]-axis represents either cost or revenue in hundreds of dollars.
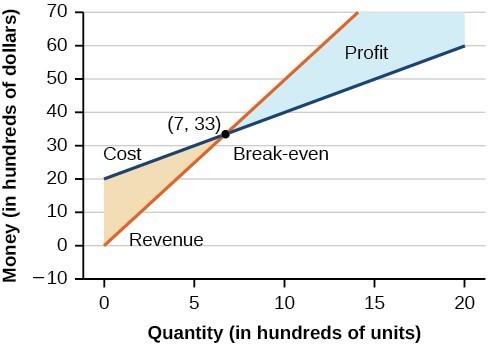
The point at which the two lines intersect is called the break-even point. We can see from the graph that if [latex]700[/latex] units are produced, the cost is [latex]\$3,300[/latex] and the revenue is also [latex]\$3,300[/latex]. In other words, the company breaks even if they produce and sell [latex]700[/latex] units. They neither make money nor lose money.
The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss. The profit function is the revenue function minus the cost function, written as [latex]P\left(x\right)=R\left(x\right)-C\left(x\right)[/latex]. Note that when [latex]R(x)=C(x),[/latex] then [latex]P(x)=0.[/latex] Clearly, knowing the quantity for which the cost equals the revenue is of great importance to businesses.
Example
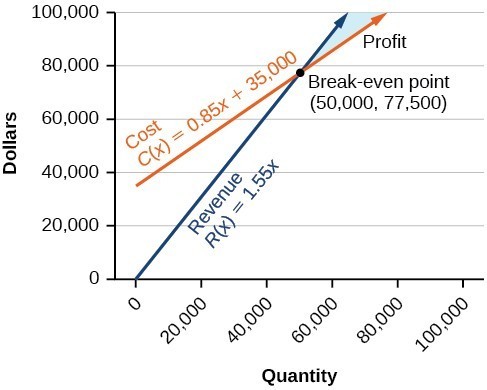
A business wants to manufacture bike frames. Before they start production, they need to make sure they can make a profit with the materials and labor force they have. Their accountant has given them a cost equation of [latex]y=0.85x+35,000[/latex] and a revenue equation of [latex]y=1.55x.[/latex]
Interpret [latex]x[/latex] and [latex]y[/latex] for the cost equation.
Interpret [latex]x[/latex] and [latex]y[/latex] for the revenue equation.
Find and interpret the break-even point for this business.
Show Solution
Cost: [latex]y=0.85x+35,000[/latex]
Revenue:[latex]y=1.55x[/latex]
The cost equation represents money leaving the company, namely how much it costs to produce a given number of bike frames. If we use the skateboard example as a model, [latex]x[/latex] would represent the number of frames produced (instead of skateboards) and [latex]y[/latex] would represent the amount of money it would cost to produce them (the same as the skateboard problem).
The revenue equation represents money coming into the company, so in this context [latex]x[/latex] still represents the number of bike frames manufactured, and [latex]y[/latex] now represents the amount of money made from selling them.
Substitution is the best method since both equations are already solved for [latex]y[/latex]. Substitute the expression [latex]0.85x+35,000[/latex] from the first equation into the second equation and solve for [latex]x[/latex].
Then, we substitute [latex]x=50,000[/latex] into either the cost function or the revenue function.
[latex]y=1.55\left(50,000\right)=77,500[/latex]
The break-even point is [latex]\left(50,000,77,500\right),[/latex] which represents [latex]50,000[/latex] bike frames sold and both cost and revenue of [latex]\$77,500.[/latex] If more than [latex]50,000[/latex] bike frames are sold, a profit will result.
Analysis of the Solution
The profit function is found using the formula [latex]P\left(x\right)=R\left(x\right)-C\left(x\right)[/latex].
The profit function is [latex]P\left(x\right)=0.7x - 35,000[/latex]. The above problem could have also been solved by setting [latex]P\left(x\right)=0[/latex] and solving. You may want to verify this yourself.
The cost to produce [latex]50,000[/latex] units is [latex]\$77,500[/latex], and the revenue from the sales of [latex]50,000[/latex] units is also [latex]\$77,500.[/latex] To make a profit, the business must produce and sell more than [latex]50,000[/latex] units.
We see from the graph below that the profit function has a negative value until [latex]x=50,000[/latex], when the graph crosses the [latex]x[/latex]-axis. Then, the graph emerges into positive y-values and continues on this path as the profit function is a straight line. This illustrates that the break-even point for businesses occurs when the profit function is [latex]0[/latex]. The area to the left of the break-even point represents operating at a loss.
Total Value Problems
In the next set of examples, we are given two types of items and multiple descriptions of their “value.” For example, we may be given two types of tickets sold at a circus and the totals of number of tickets sold as well as the total sales (or revenue).
Example
The cost of a ticket to the circus is [latex]\$25.00[/latex] for children and [latex]\$50.00[/latex] for adults. On a certain day, attendance at the circus is [latex]2,000[/latex] and the total gate revenue is [latex]\$70,000[/latex]. How many children and how many adults bought tickets?
Solution
Let [latex]c=[/latex] the number of children and [latex]a=[/latex] the number of adults in attendance.
The total number of people is [latex]2,000[/latex]. We can use this to write an equation for the number of people at the circus that day.
[latex]c+a=2,000[/latex]
The revenue from all children can be found by multiplying [latex]\$25.00[/latex] by the number of children, [latex]25c[/latex]. The revenue from all adults can be found by multiplying [latex]\$50.00[/latex] by the number of adults, [latex]50a[/latex]. The total revenue is [latex]\$70,000[/latex]. We can use this to write an equation for the revenue.
[latex]25c+50a=70,000[/latex]
We now have a system of linear equations in two variables.
In the first equation the coefficient of both variables is [latex]1[/latex] so we solve by substitution (elimination would also be possible.) We will solve the first equation for [latex]a[/latex].
We find that [latex]1,200[/latex] children and [latex]800[/latex] adults bought tickets to the circus that day.
In this video example we show how to set up a system of linear equations that represents the total cost for admission to a museum.
Try It YOURSELF
Mixture Problems
A solution is a mixture of two or more different substances like water and salt or vinegar and oil. Mixture problems are ones where two different solutions are mixed together resulting in a new final solution. Most biochemical reactions occur in liquid solutions, making them important for doctors, nurses, and researchers to understand.
The concentration or strength of a liquid solution is often described as a percentage. This number comes from the ratio of how much mass is in a specific volume of liquid. For example if you have [latex]50[/latex] grams of salt in a [latex]100[/latex] mL of water you have a [latex]50\%[/latex] salt solution based on the following ratio:
[latex]\frac{50\text{ grams }}{100\text{ mL }}=0.50\frac{\text{ grams }}{\text{ mL }}=50\text{ % }\frac{\text{ grams }}{\text{ mL }}[/latex]
Solutions used for most purposes typically come in pre-made concentrations from manufacturers, so if you need a custom concentration, you would need to mix two different strengths. For example, you may have a [latex]9\%[/latex] solution and a [latex]20\%[/latex] solution on hand, and need to mix them to create a [latex]16\%[/latex] solution.
We will use the following table to help us solve mixture problems. The units on the last row will change from problem to problem based on what the concentration is describing. In the above example, the last row would represent grams of salt.
Solution 1
Solution 2
Totals
Amount
Concentration
Value
Consider mixing the following two solutions together:
One is [latex]120[/latex] mL of a [latex]9\%\dfrac{\text{grams}}{\text{mL}}[/latex] solution,
The other is [latex]75[/latex] mL of a [latex]23\%\dfrac{\text{grams}}{\text{mL}}[/latex] solution.
Let’s determine the concentration of the resulting solution using our table. First we place the values we know into the table. Note that while the concentrations are usually given to you as percentages, we will use their decimal form when performing computations.
Solution 1
Solution 2
Totals
Amount
[latex]120[/latex] mL
[latex]75[/latex] mL
Concentration
[latex]0.09\dfrac{\text{ grams }}{\text{ mL }}[/latex]
[latex]0.23\dfrac{\text{ grams }}{\text{ mL }}[/latex]
Value
Now fill in the values in the bottom row by multiplying amount by concentration in each column.
Solution 1
Solution 2
Totals
Amount
[latex]\require{color}120[/latex] mL
[latex]75[/latex] mL
Concentration
[latex]0.09\dfrac{\text{ grams }}{\text{ mL }}[/latex]
[latex]0.23\dfrac{\text{ grams }}{\text{ mL }}[/latex]
Value
[latex]\left(120{\color{red}\cancel{\color{black}{\text{ mL}}}}\right)\left(0.09\dfrac{\text{ grams }}{{\color{red}\cancel{\color{black}{\text{ mL }}}}}\right)=10.8\text{ grams }[/latex]
[latex]\left(75\color{red}\cancel{\color{black}{\text{ mL}}}\right)\left(0.23\dfrac{\text{ grams }}{\color{red}\cancel{\color{black}{\text{ mL }}}}\right)=17.25\text{ grams }[/latex]
Finally, complete the Totals column. Our final answer is the total of the Concentration row, found by dividing totals of Value and Amount.
Solution 1
Solution 2
Totals
Amount
[latex]120[/latex] mL
[latex]75[/latex] mL
[latex]195[/latex] mL
Concentration
[latex]0.09\dfrac{\text{ grams }}{\text{ mL }}[/latex]
[latex]0.23\dfrac{\text{ grams }}{\text{ mL }}[/latex]
[latex]\frac{28.05\text{ grams }}{ 195 \text{ mL }}\approx0.14=14\text{ % }[/latex]
The final solution has a concentration of about [latex]14\%\dfrac{\text{ grams }}{\text{ mL }}[/latex]. If the context of this concentration is clear or the units are not clearly specified, we will often just say the concentration is [latex]14\%[/latex] without specifying units.
In the following examples, you will see that we can use the table to find an unknown final volume or concentration. These problems can have either one or two variables. We will start with one variable problems, then move to two variable problems.
Example
A chemist has [latex]70[/latex] mL of a [latex]50\%[/latex] methane solution. How much of an [latex]80\%[/latex] solution must she add so the final solution is [latex]60\%[/latex] methane?
Show Solution
Let’s make sure we understand the problem and the variables we will be using first before starting to write equations.
Read and Understand: We are looking for a new amount – in this case a volume – based on the words “how much”. We know two starting concentrations and the final concentration, as well as one volume.
Define and Translate: Solution 1 is the [latex]70[/latex] mL of [latex]50\%[/latex] methane and solution 2 is the unknown amount with [latex]80\%[/latex] methane. We can call our unknown amount [latex]x[/latex]. We know the final mixture has a concentration of [latex]60\%[/latex].
Write and Solve: Set up the mixture table. Remember that concentrations are written as decimals before we can perform mathematical operations on them.
Solution 1
Solution 2
Totals
Amount
[latex]70[/latex]
[latex]x[/latex]
Concentration
[latex]0.5[/latex]
[latex]0.8[/latex]
[latex]0.6[/latex]
Value (Methane)
First complete the first row by adding [latex]70+x[/latex]. Then complete the last row by multiplying Amount by Concentration in each column.
Solution 1
Solution 2
Totals
Amount
[latex]70[/latex]
[latex]x[/latex]
[latex]70+x[/latex]
Concentration
[latex]0.5[/latex]
[latex]0.8[/latex]
[latex]0.6[/latex]
Value (Methane)
[latex]70\cdot 0.5[/latex]
[latex]x\cdot 0.8[/latex]
[latex](70+x)\cdot 0.6[/latex]
The last row now represents an equation we can solve since the parts must add to the total.
[latex]\begin{align}70\cdot 0.5+x\cdot 0.8&=(70+x)\cdot 0.6\\ 35+0.8x&=42+0.6x&&\color{blue}{\textsf{simplify}}\\ 0.8x&=7+0.6x&&\color{blue}{\textsf{subtract }35\textsf{ from both sides}}\\ 0.2x&=7&&\color{blue}{\textsf{subtract }0.6x\textsf{ from both sides}}\\ x&=35&&\color{blue}{\textsf{divide by }0.2\textsf{ on both sides}}\end{align}[/latex]
We must add [latex]35[/latex] mL of the [latex]80\%[/latex] methane solution to the original [latex]70[/latex] mL of [latex]50\%[/latex] methane in order to get the desired mixture of [latex]60\%[/latex] methane.
The above problem illustrates how we can use the mixture table to define an equation to solve for an unknown volume. In the next example we will start with two known concentrations and use a system of equations to find two starting volumes necessary to achieve a specified final concentration.
Example
A farmer has two types of milk, one that is [latex]24\%[/latex] butterfat and another that is [latex]18\%[/latex] butterfat. How much of each should he use to end up with [latex]42[/latex] gallons of [latex]20\%[/latex] butterfat?
Show Solution
Read and Understand: We are asked to find two starting volumes of milk whose concentrations of butterfat are both known. We also know the final volume is [latex]42[/latex] gallons. There are two unknowns in this problem.
Define and Translate: We will call the unknown volume of the [latex]24\%[/latex] solution [latex]x[/latex], and the unknown volume of the [latex]18\%[/latex] solution [latex]y[/latex].
Write and Solve: Fill in the table with the information we know.
Solution 1
Solution 2
Totals
Amount
[latex]x[/latex]
[latex]y[/latex]
[latex]42[/latex]
Concentration
[latex]0.24[/latex]
[latex]0.18[/latex]
[latex]0.2[/latex]
Value (Butterfat)
Complete the last row by multiplying Amount by Concentration in each column.
Solution 1
Solution 2
Totals
Amount
[latex]x[/latex]
[latex]y[/latex]
[latex]42[/latex]
Concentration
[latex]0.24[/latex]
[latex]0.18[/latex]
[latex]0.2[/latex]
Value (Butterfat)
[latex]0.24x[/latex]
[latex]0.18y[/latex]
[latex]0.2\cdot42=8.4[/latex]
Remember the “Amount” row and the “Value” row represent the idea that two parts must add to a total. The first and third rows thus give us a system of equations:
We can use either substitution or elimination to solve. In this example we demonstrate the elimination method and begin by eliminating [latex]x[/latex].
We can substitute [latex]y=28[/latex] into either of the original equations to solve for [latex]x[/latex]. We use the first equation because it has easier numbers to work with.
This can be interpreted as [latex]14[/latex] gallons of [latex]24\%[/latex] butterfat milk added to [latex]28[/latex] gallons of [latex]18\%[/latex] butterfat milk will give the desired [latex]42[/latex] gallons of [latex]20\%[/latex] butterfat milk.
In the following video you will be given an example of how to solve a mixture problem without using a table, and interpret the results.
In the preceding mixture problems, our equations involved a concentration which had the form of a rate (which we wrote as a percent). Here is one more example that uses a different kind of rate.
EXAMPLE
A store owner wants to develop a new snack mix by mixing cashews and raisins. The cashews cost [latex]\$6.50[/latex] per pound and the raisins cost [latex]\$4.00[/latex] per pound. How much of each should be used to obtain [latex]40[/latex] pounds of snack mix worth [latex]\$4.75[/latex] per pound?
Show Solution
Read and Understand: We are asked to find the starting quantities of cashews and raisins with known prices per pound. The total number of final pounds and final price per pound are known.
Define and Translate: We will set [latex]c[/latex] = pounds of cashews and [latex]r[/latex] = pounds of raisins.
Write and Solve: Fill in the table with the information we know.
Solution 1
Solution 2
Totals
Amount
[latex]c[/latex]
[latex]r[/latex]
[latex]40[/latex]
Price Per Pound
[latex]6.50[/latex]
[latex]4.00[/latex]
[latex]4.75[/latex]
Value ($)
Complete the last row by multiplying Amount by Price Per Pound in each column.
Solution 1
Solution 2
Totals
Amount
[latex]c[/latex]
[latex]r[/latex]
[latex]40[/latex]
Concentration
[latex]6.50[/latex]
[latex]4.00[/latex]
[latex]4.75[/latex]
Value (Butterfat)
[latex]6.5c[/latex]
[latex]4r[/latex]
[latex]40\cdot 4.75[/latex]
Remember the “Amount” row and the “Value” row represent the idea that two parts must add to a total. The first and third rows thus give us a system of equations:
To achieve the desired mixture, the store owner needs to use [latex]12[/latex] pounds of cashews and [latex]28[/latex] pounds of raisins.
Motion Problems
In this section we will work with uniform motion, or motion with a constant speed. Uniform motion can be modeled by the following equation:
UNIFORM MOTION
If an object in uniform motion has speed [latex]r[/latex] and travels for amount of time [latex]t[/latex], the distance [latex]d[/latex] that it travels is given by
[latex]d = r \cdot t.[/latex]
Here is an example of a motion problem with two unknowns to solve for. Each object in motion results in a separate instance of the uniform motion equation.
EXAMPLE
A train leaves a station traveling north at [latex]56[/latex] km/hr. A second train leaves [latex]4[/latex] hours later traveling north on a parallel track at [latex]84[/latex] km/hr. How far from the station will the second train pass the first train?
Show Solution
Read and Understand: The trains’ speeds are known. We do not know their times but we have a relationship between the two times. We do not know the distances for either train but the distance will be equal when the second train is passing the first train.
Define and Translate: Let [latex]d[/latex] be the unknown distance from the station when the second train passes the first one. Let [latex]t[/latex] be the amount of time the second train is traveling. Hence the first train is traveling 4 hours longer, or [latex]t+4.[/latex]
Write and Solve: Fill in the table with the information we know. The table is not necessary, but can help you organize.
Distance
Rate (or speed)
Time
Train 1
[latex]d[/latex]
[latex]56[/latex]
[latex]t+4[/latex]
Train 2
[latex]d[/latex]
[latex]84[/latex]
[latex]t[/latex]
Each row represents a uniform motion, which can be modeled by [latex]d=rt.[/latex] Thus we have the system of equations
This is best solved with substitution since [latex]d[/latex] is already solved for in both equations. The substitution will effectively set the right sides equal to each other.
The second train will pass the first after [latex]8[/latex] hours. The original question asked us for the distance from the station, which is found by using [latex]t=8[/latex] in either equation, for example
[latex]d=84t=84(8)=672.[/latex]
The second train will pass the first [latex]672[/latex] km from the station.
Many real-world applications of uniform motion arise because of the effects of currents—of water or air—on the actual speed of a vehicle. Cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.
Let’s take a look at a boat travelling on a river. Depending on which way the boat is going, the current of the water is either slowing it down or speeding it up.
The images below show how a river current affects the speed at which a boat is actually travelling. We’ll call the speed of the boat in still water [latex]b[/latex] and the speed of the river current [latex]c[/latex].
The boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat’s actual speed is faster than its speed in still water. The actual speed at which the boat is moving is [latex]b+c[/latex].
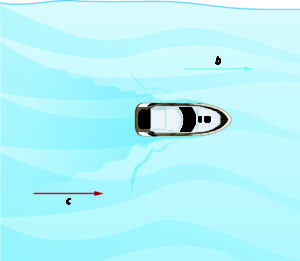
Now, the boat is going upstream, opposite to the river current. The current is going against the boat, so the boat’s actual speed is slower than its speed in still water. The actual speed of the boat is [latex]b-c[/latex]. In examples, sometimes one or both of [latex]b[/latex] and [latex]c[/latex] is given to you. It is important that [latex]b[/latex] is always first when subtracting.
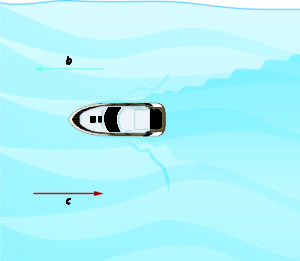
We’ll put some numbers to this situation in the next example.
EXAMPLE
Translate to a system of equations and then solve.
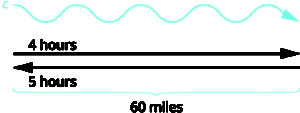
A river cruise ship sailed [latex]60[/latex] miles downstream for [latex]4[/latex] hours and then took [latex]5[/latex] hours sailing upstream to return to the dock. Find the speed of the ship in still water and the speed of the river current.
Show Answer
Read and Understand: A picture can help us visualize what is happening. Distance and time are known to us for both trips.
Define and Translate: The unknowns are the speed of the ship [latex]b[/latex] in still water and the speed of the current [latex]c,[/latex] which are the same for both trips.
A chart will help us organize the information. The ship goes downstream and then upstream. Going downstream, the current helps the ship and so the ship’s actual rate is [latex]b+c[/latex]. Going upstream, the current slows the ship and so the actual rate is [latex]b-c[/latex].
Distance
Rate (or speed)
Time
Downstream
[latex]60[/latex]
[latex]b+c[/latex]
[latex]4[/latex]
Upstream
[latex]60[/latex]
[latex]b-c[/latex]
[latex]5[/latex]
Write and Solve: Since [latex]d=rt[/latex], we can write an equation for each direction.
The boat is traveling [latex]13.5[/latex] mph in still water, and the current is [latex]1.5[/latex] mph.
In the next video, we present another example of a uniform motion problem which can be solved with a system of linear equations.
Depending on the information given in the problem, there are many different setups with which you can start a motion problem. Focus on using the table with Distance = Rate [latex]\cdot[/latex] Time, filling in any known quantities and representing unknown quantities by variables. Make sure if you know any relationships between unknown quantities, you use as few total variables as possible. Also make sure you represent Rate by two components if necessary (for example, boat speed and current with boat speed first).
Summary
Systems of equations in two variables are useful for solving a variety of application problems. They can find break-even points in business applications, solve total value problems and mixture problems, and solve for unknowns in problems of motion. Often a chart or table can be useful to organize information that is known or unknown, and also to set up the equations.
Question ID 29699. Authored by: McClure, Caren. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
Question ID 23774. Authored by: Shahbazian, Roy. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
Question ID 8589. Authored by: Greg Harbaugh. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
Question ID 2239. Authored by: Morales, Lawrence. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
Ex: System of Equations Application - Mixture Problem.. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning.. Located at: https://youtu.be/4s5MCqphpKo.. License: CC BY: Attribution
Beginning and Intermediate Algebra Textbook. . Authored by: Tyler Wallace. Located at: . License: CC BY: Attribution
