Learning Outcomes
- Investigate types of solutions to systems of equations with two variables graphically.
- Solve linear systems of equations with two variables by substitution and elimination.
- Identify inconsistent or dependent systems of equations containing two variables.
A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. To find a solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions.
For example, consider the following system of linear equations in two variables.
[latex]\begin{cases}2x+y=15\\3x-y=5\end{cases}[/latex]
A solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair [latex](4, 7)[/latex] is the solution to the system of linear equations. We can verify the solution by substituting the values [latex]\color{green}{x=4},\color{blue}{y=7}[/latex] into each equation to see if the ordered pair satisfies both equations.
[latex]\begin{array}{l}2\color{green}{\left(4\right)}+\color{blue}{\left(7\right)}=15\text{ }\text{True}\hfill \\ 3\color{green}{\left(4\right)}-\color{blue}{\left(7\right)}=5\text{ }\text{True}\hfill \end{array}[/latex]
In addition to considering the number of equations and variables, we can categorize systems of linear equations by the number of solutions. A consistent system of equations has at least one solution. A consistent system is considered to be an independent system if it has a single solution like the example we just explored. A consistent system is considered to be a dependent system if the equations are equivalent. In other words, every solution to one equation will also be a solution to the other equation. Thus, there are an infinite number of solutions.
Another type of system of linear equations is an inconsistent system which is one where the equations cannot both be true for a single ordered pair. Hence, there is no solution to the system. An easy example is
[latex]\begin{cases}x+y=3\\x+y=4\end{cases}[/latex]
Clearly, the expression [latex]x+y[/latex] cannot possibly have two different values at once.
A General Note: Types of Linear Systems
There are three types of systems of linear equations in two variables and three types of solutions.
Below are graphical representations of each type of system. It is important to understand that where the two lines cross represents an ordered pair that satisfies both equations, thus is a solution to the system.
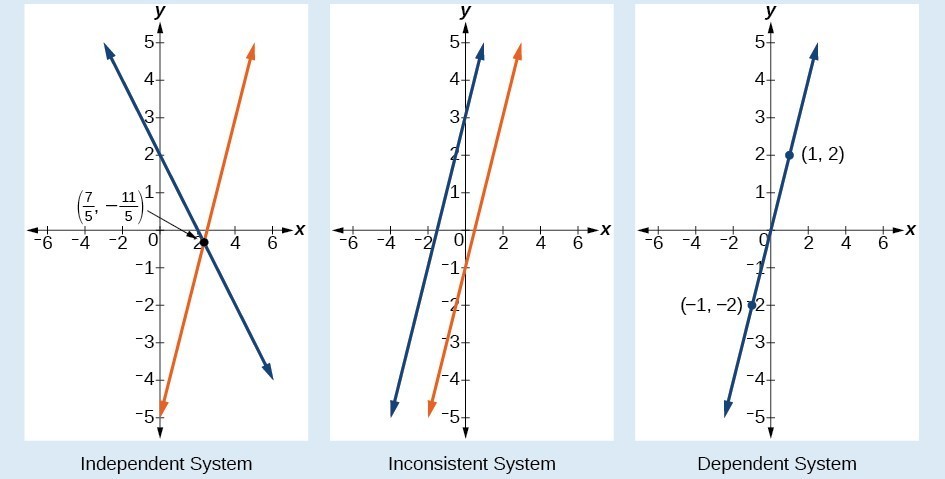
- An independent system has exactly one solution pair [latex]\left(x,y\right)[/latex]. The point where the two lines intersect is the only solution.
- An inconsistent system has no solution. The two lines are parallel and will never intersect. They have the same slope but different [latex]y[/latex]-intercepts.
- A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.
The independent and dependent systems are also consistent because they both have at least one solution.
Solving Systems of Equations by Graphing
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.
Example
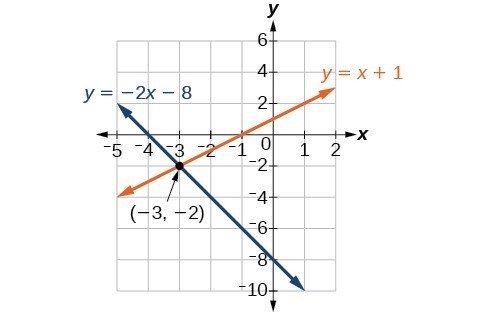
Solve the following system of equations by graphing. Identify the type of system.
[latex]\begin{cases}2x&+\ \ y=-8\\ x&-\ \ y=-1\end{cases}[/latex]
The Substitution Method
Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. We will consider two more algebraic methods of solving a system of linear equations that can always find an exact solution.
Consider the system
[latex]\begin{cases}y=2x\\x+y=12\end{cases}[/latex]
Since [latex]y[/latex] and [latex]2x[/latex] are the same quantity by the first equation, they can be used interchangeably in the problem from this point forward. Thus we can replace the [latex]\color{green}{y}[/latex] in the second equation with [latex]\color{green}{2x}.[/latex] This is called a substitution and is the basis of the substitution method. In the second equation now,
[latex]\begin{align}x+\color{green}{(2x)}&=12\\3x&=12\\x&=4\end{align}[/latex]
Once we know that [latex]x=4,[/latex] use this value in the first equation to obtain [latex]y=2(4)=8.[/latex] The system has solution [latex](4,8).[/latex]
Solving by Substitution
- Solve one of the two equations for a variable.
- Substitute the expression for this variable into the second equation, and then solve for the remaining variable.
- Use the value of the second variable to find the value of the first.
- Check the solution in both equations.
Example
Solve the following system of equations by substitution.
In the following video, you will be given an example of solving a system of two equations using the substitution method.
If you had chosen the other equation to start with in the previous example, you would still be able to find the same solution. It is really a matter of preference, because sometimes solving for a variable will result in having to work with fractions. Substitution works best if one of the variables is easily solved for.
Here is an example of what it looks like to solve an inconsistent system using substitution. We can tell it is inconsistent when we arrive at a line where there are no variables left and the numerical statement is false.
Example
Solve the following system of equations.
[latex]\left\{ \begin{array}{llll}x&=&9 &- \ \ 2y\\ x&+&2y&=\ 13 \end{array}\right.[/latex]
In the next video, we show another example of using substitution to solve a system that has no solution.
The next video illustrates what happens if solving a dependent system by substitution. This case is similar to the “no solution” case, but instead of obtaining a false statement like [latex]12=0[/latex] while solving, you obtain a true statement like [latex]12=12[/latex].
When a system is dependent, we will write our answer in set-builder notation. For example, suppose a dependent system has equation [latex]5x-2y=10.[/latex] In set builder notation, we write the solution as [latex]\left\{(x,y)\; |\; 5x-2y=10\right\}.[/latex] Remember that this indicates there are infinitely many solutions since there are infinitely many ordered pairs that satisfy the equation.
There are two things to note here. First, the left side of the notation dictates that solutions to the system have the form of ordered pairs [latex](x,y).[/latex] Second, we do not need to list the other equation that was in the system at all, since in a dependent system the two equations are equivalent to each other.
The Elimination Method
A third method of solving systems of linear equations is the elimination method. In this method, we add two equations to each other with the goal of eliminating one variable entirely. This takes advantage of the addition principle: If [latex]a=b[/latex], then [latex]a+c=b+c[/latex].
[latex]\left\{ \begin{array}{l}x+y=\text{ }5\\x-y=\text{ }11\end{array} \right.[/latex]
Consider the above system. The first equation asserts that [latex]x+y[/latex] and [latex]5[/latex] are the same quantity, so we can add [latex]\color{green}{(x+y)}[/latex] to the left side of the second equation, and [latex]\color{blue}{5}[/latex] to the right side.
[latex]\begin{array}{rl}x-y+\color{green}{(x+y)}&=11+\color{blue}{(5)}\\2x&=\text{ }16\end{array}[/latex]
Notice since the [latex]y[/latex] terms had opposite coefficients they canceled, leaving only [latex]x[/latex] to solve for. The rest of the steps are similar to the substitution process. We divide to obtain [latex]x=8,[/latex] then use this value in equation one to obtain [latex]8+y=5,[/latex] or [latex]y=-3.[/latex] The solution is the ordered pair [latex](8, -3).[/latex]
Example
Solve the given system of equations by the elimination method.
In the following video, you will see another example of how to use the method of elimination to solve a system of linear equations.
If neither the [latex]x[/latex] coefficients nor the [latex]y[/latex] coefficients are opposites to begin with, we must first multiply one or both equations by a constant. In the next example, you will see a technique where we multiply one of the equations in the system by a number that will allow us to eliminate one of the variables.
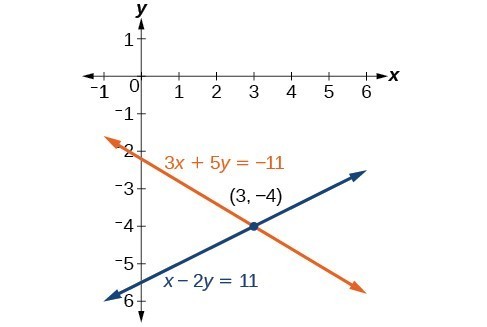
Example
Solve the given system of equations by the elimination method.
[latex]\left\{ \begin{array}{rl}3x+5y&=-11\hfill \\ x - 2y&=11\hfill \end{array} \right.[/latex]
Below is another video example of using the elimination method to solve a system of linear equations.
In the next example, we will see that sometimes both equations need to be multiplied by different numbers in order for one variable to be eliminated.
Example
Solve the given system of equations by elimination.
Did you notice in the last example that an alternative approach could have been to start by dividing equation two by [latex]5[/latex]?
In the next example, we will show how to solve a system with fractions. As with single linear equations, the easiest way to solve is to clear the fractions first with the least common denominator.
Example
Solve the given system of equations by elimination.
[latex]\left\{ \begin{array}{rl}\dfrac{x}{3}+\dfrac{y}{6}&=\text{ }3\hfill \\ \dfrac{x}{2}-\dfrac{y}{4}&=\text{ }1\hfill \end{array}\right.[/latex]
In the following video, you will find one more example of using the elimination method to solve a system; this one has coefficients that are fractions.
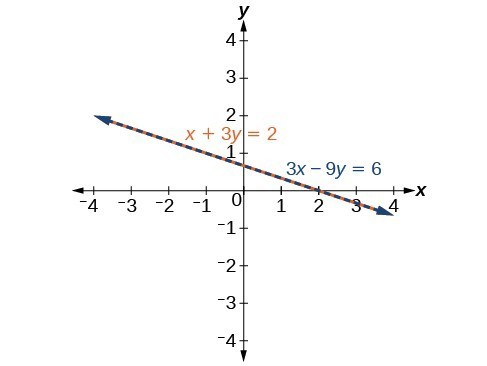
The last example includes two equations that represent the same line and are therefore dependent.
Example
Solve the given system of equations by elimination.
[latex]\left\{ \begin{array}{rl}x+3y&=\text{ }2\\ 3x+9y&=\text{ }6\end{array}\right.[/latex]
In the following video, we show another example of solving a system that is dependent using elimination.
In our last video example, we present a system that is inconsistent; it has no solutions which means the lines the equations represent are parallel to each other.
Summary
Systems of equations are typically solved algebraically by either the substitution or the elimination method. Substitution is preferred if one variable is already solved for, or if one of the variables can be easily solved for without introducing fractions. Elimination is preferred if substitution would be difficult, or if a variable would cancel upon adding the equations as they are written.
Dependent systems are represented graphically by two copies of the same line and have infinite solutions. While solving, a system is dependent if you reach an equation with no variables and a true statement. Inconsistent systems are represented graphically by two parallel lines and have no solution. While solving, a system is inconsistent if you reach an equation with no variables and a false statement.
Candela Citations
- Ex 2: Solve a System of Equations Using Substitution. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/MIXL35YRzRw. License: CC BY: Attribution
- Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
- Ex: Solve a System of Equations Using Substitution - No Solution. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/kTtKfh5gFUc. License: CC BY: Attribution
- Ex: Solve a System of Equations Using Substitution - Infinite Solutions. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/Pcqb109yK5Q. License: CC BY: Attribution
- Ex: Solve an Application Problem Using a System of Linear Equations (09x-43). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/euh9ksWrq0A. License: CC BY: Attribution
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution