Learning Outcomes
- Find the vertex, axis of symmetry, [latex]x[/latex]-intercepts (if any), [latex]y[/latex]-intercept, and/or minimum or maximum value of a factorable quadratic function in general form [latex]f(x)=ax^2+bx+c[/latex].
- Rewrite quadratic functions given in general form to vertex form.
- Graph quadratic functions in general form [latex]f(x)=ax^2+bx+c[/latex].
- Use factoring and the Zero-Product Property to solve polynomials equations, including applications.
General Form of a Quadratic Function is a function that describes a parabola, written in the form [latex]f\left(x\right)=a{x}^{2}+bx+c[/latex], where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers and [latex]a\ne 0[/latex]. If [latex]a>0[/latex], the parabola opens upward. If [latex]a<0[/latex], the parabola opens downward. We can use the general form of a parabola to find the equation of a line that is the axis of symmetry.
The vertex form and the general form of quadratic functions are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the vertex form.
For the quadratic expressions to be equal, the corresponding coefficients must be equal.
This gives us the axis of symmetry we defined earlier. Setting the constant terms equal:
In practice, though, it is usually easier to remember that [latex]k[/latex] is the output value of the function when the input is [latex]h[/latex], so [latex]k=f\left(h\right)=f\left(-\dfrac{b}{2a}\right)[/latex].
Different Forms of Quadratic Functions
A quadratic function is a function of degree two. The graph of a quadratic function is a parabola.
The general form of a quadratic function is [latex]f\left(x\right)=a{x}^{2}+bx+c[/latex] where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers and [latex]a\ne 0[/latex]. The vertex [latex](h,k)[/latex] of the parabola is located at [latex]h=\dfrac{-b}{2a}, \text{ }k=f\left(\dfrac{-b}{2a}\right)[/latex].
We learned in section 3.3, the vertex form of a quadratic function is [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]. Where the vertex is [latex]\left(h,k\right)[/latex].
We learned in section 3.4, the intercept form of a quadratic function is [latex]f(x)=a(x-p)(x-q)[/latex]. Where [latex]p[/latex] and [latex]q[/latex] are the [latex]x[/latex]-intercepts of the graph and the vertex is half-way between the [latex]x[/latex]-intercepts.
The axis of symmetry is defined by the line [latex]x=\dfrac{-b}{2a}[/latex]. If we use factoring to solve [latex]a{x}^{2}+bx+c=0[/latex] for the [latex]x[/latex]-intercepts, or zeros, we find the value of [latex]x[/latex] halfway between them is always [latex]x=\dfrac{-b}{2a}[/latex], the equation for the axis of symmetry.
Figure 1 shows the graph of the quadratic function written in general form as [latex]y={x}^{2}+4x+3[/latex]. In this form, [latex]a=1,\text{ }b=4[/latex], and [latex]c=3[/latex]. Because [latex]a>0[/latex], the parabola opens upward. The axis of symmetry is [latex]x=\dfrac{-4}{2\left(1\right)}=-2[/latex]. This makes sense because we can see from the graph that the vertical line [latex]x=-2[/latex] divides the graph in half.
The vertex always occurs along the axis of symmetry. We have found the [latex]x[/latex]-coordinate of the vertex to be [latex]-2[/latex]. To find the [latex]y[/latex]-coordinate of the vertex we need to substitute [latex]-2[/latex] in place of [latex]x[/latex] and solve for [latex]y[/latex].
[latex]\begin{align}\require{color} y &= x^2+4x+3\\ y &= (\color{Green}{-2}\color{black}{)^2+4(}\color{Green}{-2}\color{black}{)+3}\\ y &=4+(-8)+3\\ y &= -1\end{align}[/latex]
In this instance, [latex]\left(-2,-1\right)[/latex] is the vertex. This parabola opens upward, so the vertex occurs at the lowest point on the graph, also called the minimum point of the graph. The vertex [latex](-2,-1)[/latex] is the minimum point on this graph.
The [latex]x[/latex]-intercepts are the point(s) where the parabola crosses the [latex]x[/latex]-axis, these can be found by letting [latex]y=0[/latex] and solving for [latex]x[/latex]. We will use factoring and the Zero-Product Property to solve for [latex]x[/latex].
[latex]\begin{align} y &= x^2+4x+3\\ 0 &=x^2+4x+3 && \color{blue}{\textsf{Which two numbers multiply to be 3 and add to be 4?}} \\ 0 &=(x+3)(x+1) && \color{blue}{\textsf{set each factor equal to zero and solve}}\\ x+3 &=0 \quad x+1 =0\\ x &= -3 \quad x=-1 \end{align}[/latex]
The [latex]x[/latex]-intercepts occur at [latex]\left(-3,0\right)[/latex] and [latex]\left(-1,0\right)[/latex].
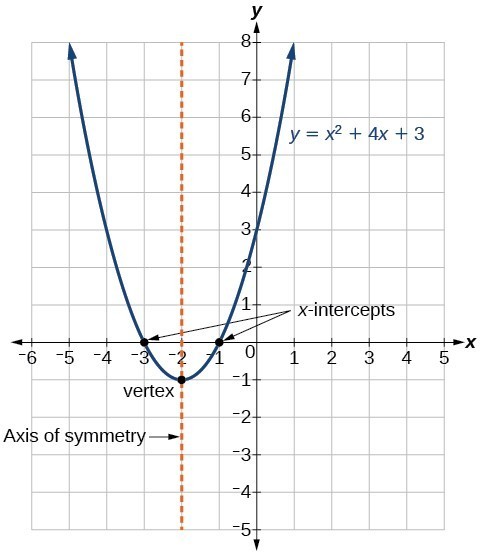
Figure 1
How To: find the vertex when given a quadratic function in general form
- Identify [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex].
- Find [latex]h[/latex], the [latex]x[/latex]-coordinate of the vertex, by substituting [latex]a[/latex] and [latex]b[/latex] into [latex]h=\dfrac{-b}{2a}[/latex].
- Find [latex]k[/latex], the [latex]y[/latex]-coordinate of the vertex, by evaluating [latex]k=f\left(h\right)=f\left(\dfrac{-b}{2a}\right)[/latex].
Example
Find the vertex of the quadratic function [latex]f\left(x\right)=2{x}^{2}-8x+7[/latex]. Rewrite the quadratic function in vertex form.
Try It
Given the function [latex]g\left(x\right)=13+{x}^{2}-6x[/latex], write the function in general form and then in vertex form.
Solve Quadratic Equations using Factoring and the Zero-Product Property
Let us start with an example that factors a GCF from a binomial and apply the Zero-Product Property to solve a polynomial equation.
Example
Solve: [latex]-t^2+t=0[/latex]
In the following video, we show two more examples of using both factoring and the Zero-Product Property to solve a quadratic equation.
In the next video, we show that you can use previously learned methods to factor a trinomial in order to solve a quadratic equation.
We will now solve a quadratic equation where it is not set equal to zero on one side.
Example
Solve: [latex]x^2-4x=5[/latex]
The following binomial is a difference of squares and can be factored. Factor the binomial and use the zero-product property to solve.
Example
Solve using the Zero-Product Property: [latex]{x}^{2}-9=0[/latex].
Here are some video examples in which you can use factoring to solve these quadratic equations.
Example
Use factoring and the Zero-Product Property to solve the quadratic equation: [latex]4{x}^{2}+15x+9=0[/latex].
The following video examples can be factored but the leading coefficients is NOT 1.
Graph quadratic functions in general form [latex]f(x)=ax^2+bx+c[/latex]
To graph quadratic functions in general form, we will first find the vertex, axis of symmetry, [latex]x[/latex]-intercept(s), and the [latex]y[/latex]-intercept. We will graph the function, [latex]g(x)=-x^2-8x-15[/latex] where [latex]a=-1[/latex], [latex]b=-8[/latex], and [latex]c=-15[/latex].
Start by finding the vertex. The [latex]x[/latex]-coordinate of the vertex:
[latex]\begin{align} h &=\dfrac{-b}{2a} \\ h &=\dfrac{-(-8)}{2\left(-1\right)} \\ h &=\dfrac{8}{-2} \\ h &=-4 \end{align}[/latex]
The [latex]y[/latex]-coordinate of the vertex:
[latex]\begin{align}k &= f(h) \\ k &= f(-4) \\ k &= -(-4)^2-8(-4)-15 \\ k &= -16+32-15\\ k &=1 \end{align}[/latex]
The vertex is [latex](-4,1)[/latex].
The axis of symmetry is a vertical line that passes through the vertex. In this case the axis (line) of symmetry is [latex]x=-4[/latex].
We can rewrite the equation as [latex]y=-x^2-8x-15[/latex]. To find the [latex]y[/latex]-intercept, let [latex]x=0[/latex] and solve for [latex]y[/latex].
[latex]\begin{align} y &= -x^2-8x-15\\ y &= -(0)^2-8(0)-15\\ y &= -15\end{align}[/latex]
The [latex]y[/latex]-intercept is [latex](0,-15)[/latex].
To find the [latex]x[/latex]-intercept(s), let [latex]y=0[/latex] and solve for [latex]x[/latex]. We will use factoring and the Zero-Product Property to find the [latex]x[/latex]-intercept(s).
[latex]\begin{align} y &= -x^2-8x-15\\ 0 &= -x^2-8x-15\\ 0 &= -1(x^2+8x+15)\\ 0 &= -1(x+3)(x+5)\end{align}[/latex]
[latex]x+3=0 \hspace{1.5cm} x+5=0[/latex]
[latex]x = -3\hspace{2cm} x = -5[/latex]
The [latex]x[/latex]-intercepts are [latex](-3,0)[/latex] and [latex](-5,0)[/latex].
Figure 2 is the graph of the function [latex]g(x)=-x^2-8x-15[/latex].
Figure 2
NOTE: If the [latex]x[/latex]-intercepts do not exist or the quadratic equation cannot be factored to solve or if the [latex]y[/latex]-intercept is off the grid that you are being asked to graph on, you can make a table of values to help you find additional point(s) on the graph. You can pick [latex]x[/latex] values that are on either side of the vertex, for this example we could pick [latex]x=-2[/latex] and [latex]x=-6[/latex].
| [latex]x[/latex] | [latex]y=-x^2-8x-15[/latex] |
|---|---|
| [latex]-2[/latex] | [latex]\begin{align} y &= -1(\color{Green}{-2}\color{black}{)^2-8}(\color{Green}{-2}\color{black}{)-15}\\ &= -1(4)+16-15\\ &= -3 \end{align}[/latex] |
| [latex]-6[/latex] | [latex]\begin{align} y &= -1(\color{Green}{-6}\color{black}{)^2-8}(\color{Green}{-6}\color{black}{)-15}\\ &= -1(36)+48-15\\ &= -3 \end{align}[/latex] |
Example
Graph [latex]f(x)=2x^2-4x+3[/latex] by first finding the vertex, axis of symmetry, [latex]y[/latex]-intercept, and [latex]x[/latex]-intercept(s).
Solving Applications of Quadratic Functions
There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue. Remember when [latex]a>0[/latex], the graph of a parabola opens upward and the vertex is the lowest point on the graph or the minimum. When [latex]a<0[/latex], the graph of a parabola opens downward and the vertex is the highest point on the graph or the maximum.

Figure 3
Projectile motion happens when you throw a ball into the air and it comes back down because of gravity. A projectile will follow a curved path that behaves in a predictable way. This predictable motion has been studied for centuries, and in simple cases, an object’s height from the ground at a given time, [latex]t[/latex], can be modeled with a polynomial function of the form [latex]h(t)=at^2+bt+c[/latex], where [latex]h(t) =[/latex] height of an object at a given time, [latex]t[/latex]. Projectile motion is also called a parabolic trajectory because of the shape of the path of a projectile’s motion, as in the water in the image of the fountain below. Parabolic motion and its related functions allow us to launch satellites for telecommunications and rockets for space exploration.

Parabolic water trajectory in a fountain.
Example
A small toy rocket is launched from a [latex]4[/latex]-foot pedestal. The height ([latex]h[/latex], in feet) of the rocket [latex]t[/latex] seconds after taking off is given by the function [latex]h(t)=−2t^{2}+7t+4[/latex]. How long will it take the rocket to hit the ground?
In the next example, we will solve for the time that the rocket reaches a given height other than zero.
Example
Use the formula for the height of the rocket in the previous example to find the time when the rocket is [latex]4[/latex] feet from hitting the ground on its way back down. Refer to the image.
[latex]h(t)=−2t^{2}+7t+4[/latex]
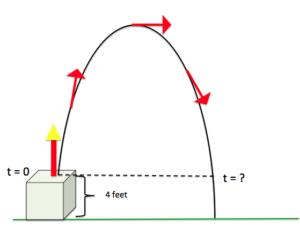
In the following video, we show another example of how to find the time when a object following a parabolic trajectory hits the ground.
In this section we introduced the concept of projectile motion and showed that it can be modeled with quadratic functions. While the models used in these examples can be factored, that is not always the case with these types of applications. The concepts and interpretations are the same as what would happen in “real life.”
Exercises
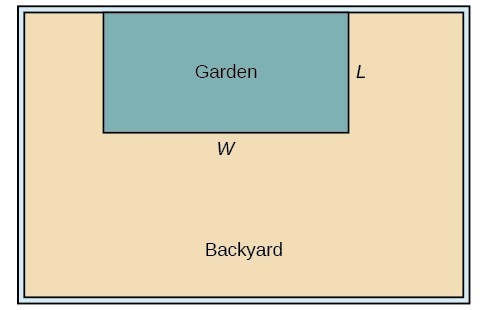
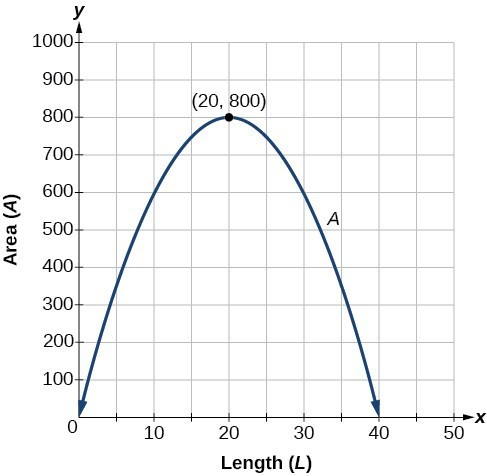
A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased [latex]80[/latex] feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.
- Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length [latex]L[/latex].
- What dimensions should she make her garden to maximize the enclosed area?
Example
A ball is thrown upward from the top of a [latex]40[/latex]-foot high building at a speed of [latex]80[/latex] feet per second. The ball’s height above ground can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+80t+40[/latex].
a. When does the ball reach the maximum height?
b. What is the maximum height of the ball?
Key Equations
| Vertex form of a quadratic function | [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] |
| Intercept form of a quadratic function | [latex]f(x)=(x-p)(x-q)[/latex] |
| General form of a quadratic function | [latex]f\left(x\right)=a{x}^{2}+bx+c[/latex] |
Summary
You can rewrite a quadratic function that is given in general form [latex]f(x)=ax^2+bx+c[/latex] in vertex form [latex]f(x)=a(x-h)^2+k[/latex].
You can find the vertex, axis of symmetry, [latex]y[/latex]-intercept, and [latex]x[/latex]-intercepts (if any) of a quadratic function in general form and use those points to graph the parabola.
You can find the solutions, or roots, of quadratic equations in general form by setting one side equal to zero, factoring the quadratic, and then applying the Zero-Product Property. The Zero-Product Property states that if [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both [latex]a[/latex] and [latex]b[/latex] are [latex]0[/latex]. Once the polynomial is factored, set each factor equal to zero and solve them separately. The answers will be the set of solutions for the original equation.
Not all solutions are appropriate for some applications. For example, in many real-world situations, negative solutions are not appropriate and must be discarded.
Candela Citations
- Solve a Quadratic Equations with Fractions by Factoring (a not 1). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/kDj_qdKW-ls. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex: Factor and Solve Quadratic Equation - Greatest Common Factor Only. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/gIwMkTAclw8. License: CC BY: Attribution
- Ex: Factor and Solve Quadratic Equations When A equals 1. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/bi7i_RuIGl0. License: CC BY: Attribution
- Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution


Try It
A rock is thrown upward from the top of a [latex]112[/latex]-foot high cliff overlooking the ocean at a speed of [latex]96[/latex] feet per second. The rock’s height above ocean can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+96t+112[/latex], where [latex]H[/latex] is the height in feet and [latex]t[/latex] is time after the throw in seconds.
a. When does the rock reach the maximum height?
b. What is the maximum height of the rock?
c. When does the rock hit the ocean?
a. 3 seconds b. 256 feet c. 7 seconds
Explanation:
a. The rock reaches the maximum height at the vertex of the parabola.
[latex]\begin{align} h&=\dfrac{-96}{2\left(-16\right)}\\ h&=\dfrac{-96}{-32} \\ h&= 3 \end{align}[/latex]
The rock reaches a maximum height at [latex]3[/latex] seconds.
b. To find the maximum height, find the [latex]y[/latex]-coordinate of the vertex of the parabola.
[latex]\begin{align}k&=-16{\left(3\right)}^{2}+96\left(3\right)+112 \\ k&=256 \end{align}[/latex]
The rock reaches a maximum height of [latex]256[/latex] feet.
c. To find when the rock hits the ocean, we need to find when the height, [latex]H(t)[/latex] equals [latex]0[/latex]. We factor to solve for [latex]t[/latex].
[latex]\begin{align} H(t) &= -16t^2+96t+112\\ 0 &= -16t^2+96t+112\\ 0 &= -16(t^2-6t-7)\\ 0 &= -16(t+1)(t-7) \end{align}[/latex]
[latex]t+1=0[/latex] or [latex]t-7=0[/latex]
[latex]t = -1[/latex] or [latex]t = 7[/latex]
Since [latex]t[/latex] represents time, it cannot be a negative number; only [latex]t=7[/latex] makes sense in this context.
The rock hits the ocean [latex]7[/latex] seconds after it is thrown.