Learning OutcomeS
- Determine the number and type (rational, irrational, or complex) of solutions of a quadratic equation using the discriminant.
- Write a quadratic equation given all integer or rational solutions
The Discriminant
The quadratic formula not only generates the solutions to a quadratic equation, but also tells us about the nature of the solutions. When we consider the discriminant, or the expression under the radical, [latex]{b}^{2}-4ac[/latex], it tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to expect.
Let us explore how the discriminant affects the evaluation of [latex]\sqrt{{{b}^{2}}-4ac}[/latex] in the quadratic formula and how it helps to determine the solution set.
- If [latex]b^{2}-4ac>0[/latex], then the number underneath the radical will be a positive value. You can always find the square root of a positive number, so evaluating the quadratic formula will result in two real solutions (one by adding the positive square root and one by subtracting it).
- If [latex]b^{2}-4ac=0[/latex], then you will be taking the square root of [latex]0[/latex], which is [latex]0[/latex]. Since adding and subtracting [latex]0[/latex] both give the same result, the “[latex]\pm[/latex]” portion of the formula does not matter. There will be one real repeated solution.
- If [latex]b^{2}-4ac<0[/latex], then the number underneath the radical will be a negative value. Since you cannot find the square root of a negative number using real numbers, there are no real solutions. However, you can use imaginary numbers. You will then have two complex solutions, one by adding the imaginary square root and one by subtracting it.
The table below summarizes the relationship between the value of the discriminant and the solutions of a quadratic equation.
| Value of Discriminant | Results |
|---|---|
| [latex]{b}^{2}-4ac=0[/latex] | One repeated rational solution |
| [latex]{b}^{2}-4ac>0[/latex], perfect square | Two rational solutions |
| [latex]{b}^{2}-4ac>0[/latex], not a perfect square | Two irrational solutions |
| [latex]{b}^{2}-4ac<0[/latex] | Two complex solutions |
A General Note: The Discriminant
For [latex]a{x}^{2}+bx+c=0[/latex], where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers, the discriminant is the expression under the radical in the quadratic formula: [latex]{b}^{2}-4ac[/latex]. It tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to expect.
Example
Use the discriminant to find the nature of the solutions to the following quadratic equations:
- [latex]{x}^{2}+4x+4=0[/latex]
- [latex]8{x}^{2}+14x+3=0[/latex]
- [latex]3{x}^{2}-5x - 2=0[/latex]
- [latex]3{x}^{2}-10x+15=0[/latex]
Example
Use the discriminant to determine how many and what kind of solutions the quadratic equation [latex]x^{2}-4x+10=0[/latex] has.
In the last example, we will draw a correlation between the number and type of solutions to a quadratic equation and the graph of its corresponding function.
Example
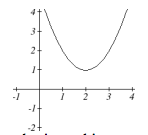
Use the following graphs of quadratic functions to determine how many and what type of solutions the corresponding quadratic equation [latex]f(x)=0[/latex] will have. Determine whether the discriminant will be greater than, less than, or equal to zero for each.
a.
b.
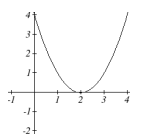
c.
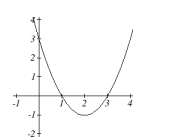
We can summarize our results as follows:
| Discriminant | Number and Type of Solutions | Graph of Quadratic Function |
| [latex]b^{2}-4ac<0[/latex] | two complex solutions | will not cross the x-axis |
| [latex]b^{2}-4ac=0[/latex] | one real repeated solution | will touch x-axis once |
| [latex]b^{2}-4ac>0[/latex] | two real solutions | will cross x-axis twice |
In the following video, we show more examples of how to use the discriminant to describe the type of solutions of a quadratic equation.
Creating an Equation from Given Solutions
There are many situations, particularly in modeling applications, where we want to create a quadratic equation that has certain solutions. The key to this process is to work backward from how we usually find solutions to a quadratic equation.
As an example, consider the following solution to a factorable quadratic equation:
[latex]\begin{align}x^2+6x-16&=0\\ (x+8)(x-2)&=0\\ x+8=0 \textsf{ or } x-2 = 0&\\ x=-8 \textsf{ or } x=2& \end{align}[/latex]
If we start with the two solutions, we should be able to easily reverse the steps in the problem. This consists of first writing a factor corresponding to each given solution, then multiplying the factors to create an equation. Here is a quick example with given solutions [latex]x=5[/latex] and [latex]x=6[/latex]:
[latex]\begin{align}x=5 \textsf{ or } x=6&\\ x-5=0 \textsf{ or } x-6 = 0&\\ (x-5)(x-6)&=0\\ x^2-11x+30&=0 \end{align}[/latex]
The first two steps can be skipped by simply writing a factor [latex](x-c)[/latex] for each given solution [latex]c[/latex].
EXAMPLE
Find the equation, in standard form [latex]y=ax^2+bx+c[/latex], for a quadratic that has roots at [latex]x=-3[/latex] and [latex]x=7[/latex], and has leading coefficient [latex]1[/latex].
The reason we have to specify “leading coefficient [latex]1[/latex]” is because after setting up our factored expression [latex](x+3)(x-7)=0[/latex], we could easily add any coefficient we choose to the left side and the given solutions will still be the same. For example, [latex]2(x+3)(x-7)=0[/latex] still has solutions [latex]x=-3[/latex] and [latex]x=7[/latex], but will have a leading coefficient of [latex]2[/latex] when multiplied out.
EXAMPLE
Find the equation, in standard form [latex]y=ax^2+bx+c[/latex], for a quadratic that has roots at [latex]x=\dfrac{1}{2}[/latex] and [latex]x=-\dfrac{2}{5}[/latex]. Write an equation with integer coefficients and minimal leading coefficient.
Summary
The discriminant of the quadratic formula is the quantity under the radical, [latex]{{b}^{2}}-4ac[/latex]. It determines the number and the type of solutions that a quadratic equation has. If the discriminant is positive, there are [latex]2[/latex] real solutions. If it is [latex]0[/latex], there is [latex]1[/latex] real repeated solution. If the discriminant is negative, there are [latex]2[/latex] complex solutions (but no real solutions).
We can create a quadratic equation with given solutions by creating a factor [latex](x-c)[/latex] for each solution [latex]x=c[/latex] that the equation is required to have. When a quadratic equation in standard form [latex]y=ax^2+bx+c[/latex] is set equal to [latex]0[/latex], the solutions are called roots. These give the [latex]x[/latex]-coordinates of the [latex]x[/latex]-intercepts of the parabola.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex: The Discriminant. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/hSWs0VUyn1k. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution
