6.5 Problem Solving and Quadratic Functions

Learning Outcomes

  • Solve maximum and minimum applications by finding the vertex of a given quadratic function.
  • Find the x-intercepts of a quadratic function which is not factorable.
  • Solve applications modeled by quadratic functions.

In this section, we will expand upon the previous examples we’ve done involving quadratic functions using our new methods of solving quadratic equations. We will also take this time to review the graphing process and some of our key applications.

Finding the x-intercepts of a quadratic function

Finding intercepts of quadratic functions can be useful both for the purpose of graphing and in certain application problems. Recall that we find the [latex]y[/latex]-intercept of a quadratic function by evaluating the function at an input of zero, and we find the [latex]x[/latex]-intercepts at locations where the output is zero. Notice that the number of [latex]x[/latex]-intercepts can vary depending upon the location of the graph.

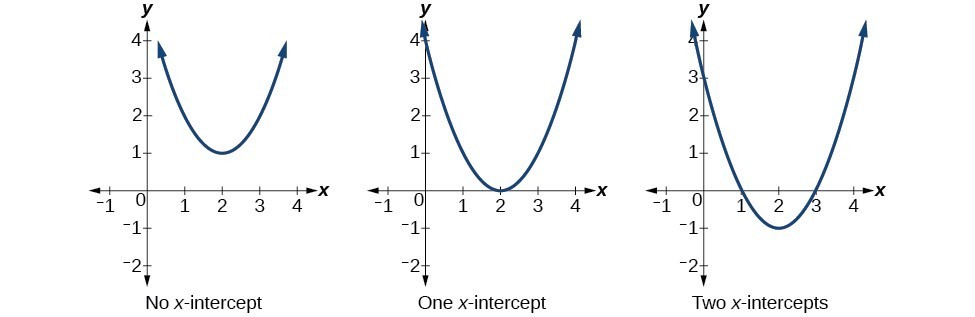
Three graphs where the first graph shows a parabola with no x-intercept, the second is a parabola with one –intercept, and the third parabola is of two x-intercepts.

Figure 13. Number of x-intercepts of a parabola

How To: Given a quadratic function [latex]f\left(x\right)[/latex], find the y– and x-intercepts.

  1. Evaluate [latex]f\left(0\right)[/latex] to find the y-intercept.
  2. Solve the quadratic equation [latex]f\left(x\right)=0[/latex] to find the x-intercepts.

Example 7: Finding the y– and x-Intercepts of a Parabola

Find the y– and x-intercepts of the quadratic [latex]f\left(x\right)=3{x}^{2}+5x - 2[/latex].

  • The minimum or maximum value of a quadratic function can be used to determine the range of the function and to solve many kinds of real-world problems, including problems involving area and revenue.
  • The vertex and the intercepts can be identified and interpreted to solve real-world problems.

Solve problems involving a quadratic function’s minimum or maximum value

In Example 7, the quadratic was easily solved by factoring. However, there are many quadratics that cannot be factored. We can solve these quadratics by first rewriting them in standard form.

How To: Given a quadratic function, find the x-intercepts by rewriting in standard form.

  1. Substitute a and b into [latex]h=-\frac{b}{2a}[/latex].
  2. Substitute x = h into the general form of the quadratic function to find k.
  3. Rewrite the quadratic in standard form using h and k.
  4. Solve for when the output of the function will be zero to find the x-intercepts.

Example 8: Finding the x-Intercepts of a Parabola

Find the x-intercepts of the quadratic function [latex]f\left(x\right)=2{x}^{2}+4x - 4[/latex].

try it