A quadratic inequality is a quadratic equation, but with the equal sign replaced by an inequality sign. An example of a quadratic inequality is

[latex]x^2-3x-4\leq 0[/latex]

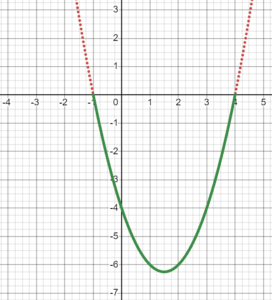
To help solve this, we will consider the quadratic function [latex]f(x)=x^2-3x-4[/latex]. Solving our inequality above is equivalent to asking which [latex] x [/latex] values cause the output value of the function [latex] f [/latex] to be less than or equal to [latex] 0 [/latex]. We will use a graph of the function [latex] f [/latex] to understand this idea. Below is the graph of the function [latex] f [/latex]. Note that the function factors as [latex]f(x)=(x-4)(x+1)[/latex], which reveals the two [latex] x [/latex]-intercepts of [latex] (-1,0) [/latex] and [latex] (4, 0) [/latex].

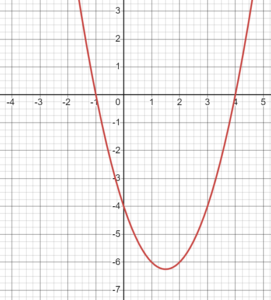
Try to use the above graph to solve the inequality [latex] f(x) \leq 0 [/latex] before revealing the answer below.

Try It

Solve the inequality [latex]x^2-3x-4\leq 0[/latex] by graphing.

Show Solution

The solution to the inequality is the portion of the graph of [latex]f(x)=x^2-3x-4[/latex] which has outputs less than or equal to [latex] 0 [/latex], which in the graph is the portion of the curve touching or below the [latex] x [/latex]-axis. We can determine visually that [latex] x [/latex] values between [latex] -1 [/latex] and [latex] 4 [/latex] (and including these two numbers) satisfy this condition. Here is the same graph, but with the portion below the [latex] x [/latex]-axis colored in green and the portion above the graph dotted:

The solution is the interval of [latex] x [/latex]-values corresponding to the region below or touching the [latex] x [/latex]-axis, which is the interval [latex] [-1,4] [/latex].

We can see from the above example that the key was to use the places where the graph crosses the [latex] x [/latex]-axis as the endpoints of our solution interval.

Here is another example to try. Note the small differences in the setup of the problem.

EXAMPLE

Solve the inequality [latex]x^2-6x+8 > 0[/latex].

Show Solution

The function [latex]f(x)=x^2-6x+8[/latex] factors as [latex]f(x)=(x-4)(x-2)[/latex] and so the [latex] x [/latex]-intercepts are at [latex] (4,0) [/latex] and [latex] (2,0) [/latex]. Since the leading coefficient is positive, we draw an upward facing parabola. This gives us enough information to sketch a graph.

Since we are solving [latex] f(x) > 0 [/latex], we are interested in the portion of the graph that is above the [latex] x [/latex]-axis this time. Here is the same graph, but with the portion above the graph shaded green and the portion below dotted.

There are two intervals of [latex] x [/latex]-values that correspond to portions of the graph above the [latex] x [/latex]-axis. These intervals consist of [latex] x [/latex] values less than [latex] 2 [/latex] and [latex] x [/latex] values greater than [latex] 4 [/latex], since these are the [latex] x [/latex]-intercepts of the graph. Since we have strict inequality in this example, the values [latex] x=2 [/latex] and [latex] x=4 [/latex] are not solutions.

The solution is [latex] (-\infty, 2) \cup (4, \infty) [/latex].

Using a Number Line

We can see from the above examples that the [latex] x [/latex]-intercepts of the function associated with the inequality are crucial to the solving process and end up being the endpoints of the solution intervals. This is because a parabola is a smooth curve and can only pass from above to below the [latex] x [/latex]-axis by passing through the axis first (resulting in an intercept).

This suggests an alternative approach to solving which does not require graphing the parabola. We can determine the “boundary values” where the inequality can pass from being true to false, then use test points to determine which intervals on the number line are true or false. This is similar to the test point approach used in solving systems of inequalities in Chapter 2.

Consider the inequality [latex]x^2+2x-15>0[/latex]. Solving the related equation [latex]x^2+2x-15=0[/latex] gives us the boundary values which separate solutions from non-solutions on the number line.  This equation can be solved by factoring:

[latex]\begin{align}x^2+2x-15&=0\\ (x+5)(x-3)&=0\\ x+5=0 \textsf{ or } x-3&=0\\ x=-5 \textsf{ or } x&=3 \end{align}[/latex]

Thus the inequality can switch from being true to false or false to true at these two values. We can test [latex] x [/latex] values in each of the three number line regions separated by these boundary values to determine if each interval represents solutions or non-solutions.

Number line for testing values

The big dots represent the boundary values and the red Xs represent the test points we will use.

Substituting each test value in the original inequality [latex]x^2+2x-15>0[/latex],

Test [latex] -6 [/latex]: [latex](-6)^2+2(-6)-15 > 0[/latex], or [latex] 9>0 [/latex] which is TRUE.

Test [latex] 0 [/latex]: [latex](0)^2+2(0)-15 > 0[/latex], or [latex] -15>0 [/latex] which is FALSE.

Test [latex] 4 [/latex]: [latex](4)^2+2(4)-15 > 0[/latex], or [latex] 9>0 [/latex] which is TRUE.

Thus the solution is [latex] (-\infty, -5) \cup (3, \infty) [/latex], using parentheses at the boundary values because the inequality was strict.

Let’s try a few more examples using this approach.

EXAMPLE

Solve the inequality [latex]x^2 \leq 4x + 5[/latex].

Show Solution

We should first rewrite the inequality with [latex] 0 [/latex] on the right side to prepare to factor.

[latex]x^2 - 4x - 5 \leq 0[/latex]

Now solve for the boundary values by solving the related equation:

[latex]\begin{align}x^2 - 4x - 5 &= 0\\ (x-5)(x+1) &= 0\\ x-5=0 \textsf{ or } x+1&=0\\ x=5 \textsf{ or } x=-1\end{align}[/latex]

The boundary values are [latex] x=5 [/latex] and [latex] x=-1 [/latex]. This divides the number line into three distinct intervals. We test a number inside each interval in the original inequality (you could also test it in the inequality solved for 0):

Test [latex] -2 [/latex] from the left interval:  [latex] (-2)^2 \leq 4(-2)+5 [/latex], or [latex] 4 \leq -3 [/latex] which is FALSE.

Test [latex] 0 [/latex] from the middle interval:  [latex] (0)^2 \leq 4(0)+5 [/latex], or [latex] 0 \leq 5 [/latex] which is TRUE.

Test [latex] 6 [/latex] from the right interval:  [latex] (6)^2 \leq 4(6)+5 [/latex], or [latex] 36 \leq 29 [/latex] which is FALSE.

Thus the solution is the interval [latex] [-1, 5] [/latex], including the boundary points because equality is allowed in this inequality.

You may have noticed a pattern of the intervals alternating between true and false. Though this is a keen observation, the next example will prove this is not always the case!

EXAMPLE

Solve the inequality [latex]2x^2+8x+8 > 0[/latex].

Show Solution

Begin by solving for boundary values using the related equation:

[latex]\begin{align}2x^2+8x+8 &= 0\\ 2(x^2+4x+4) &= 0\\ 2(x+2)(x+2) &= 0\\ x+2 &= 0\\ x&=-2\end{align}[/latex]

There is only one boundary value of [latex] x=-2 [/latex] this time because the polynomial to factor was a perfect square trinomial. Our number line has only two intervals to test with one boundary value separating them.

Test [latex] -3 [/latex] from the left interval:  [latex] 2(-3)^2 + 8(-3) + 8 > 0 [/latex], or [latex] 2 > 0 [/latex] which is TRUE.

Test [latex] 0 [/latex] from the right interval:  [latex] 2(0)^2 + 8(0) + 8 > 0 [/latex], or [latex] 8 > 0 [/latex] which is TRUE.

Both intervals consist of solutions this time! The only number which is NOT a solution is the boundary value of [latex] x=-2 [/latex] since the inequality was strict. Thus the solution set is [latex] (-\infty, -2) \cup (-2, \infty) [/latex].

The boundary value and test point method for solving quadratic inequalities will be more generally useful for you in future math courses, where you may solve polynomial or rational inequalities.

Summary

A quadratic inequality can be solved by two different methods. First make sure [latex] 0 [/latex] is on one side of the inequality.

One method is to graph the corresponding parabola and determine for which [latex] x [/latex]-values the parabola is above or below the [latex] x [/latex]-axis.

The other method is to find the endpoints of the solution intervals, called boundary values, by turning the inequality into an equation and solving. Separate the number line into intervals using the boundary values. We can test each resulting interval using a test point to determine whether that interval is in the solution set or not.