Learning Outcomes
- Find the equation of a circle in standard form given the center and radius.
- Find the center and radius of a circle given the equation in standard form.
- Find the equation of a circle in standard form given the center and a point on the circle.
- Given the general form of the equation of a circle, write the equation in standard form by completing the square.
- Graph a circle given the center and radius or given the equation.
DEFINITION OF A CIRCLE
A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, [latex](h,k)[/latex], and the fixed distance is called the radius, [latex]r[/latex], of the circle.
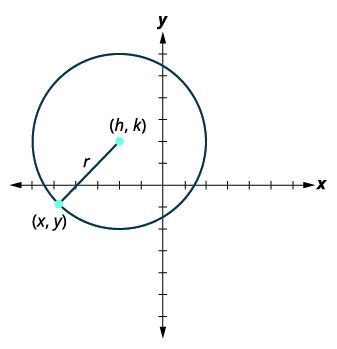
DERIVING THE STANDARD FORM OF A CIRCLE
To derive the equation of a circle, we can use the distance formula with the points [latex](h,k)[/latex], [latex](x,y)[/latex], and the distance [latex]r[/latex].
Substitute the values.
Square both sides.
STANDARD FORM OF A CIRCLE
The standard form of a circle is as follows:
[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]
Write the Equation of a Circle in Standard Form
Example 1: WRITE THE STANDARD FORM Equation OF A CIRCLE
Write the standard form of a circle with radius [latex]3[/latex] and center [latex](0,0)[/latex].
Use the standard form of a circle.
[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]
Substitute in the values [latex]r=3, h=0, k=0[/latex].
[latex]{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}=3^{2}[/latex]
Simplify.
[latex]{x}^{2}+{y}^{2}=9[/latex]
Example 2: WRITE THE STANDARD FORM equation OF A CIRCLE
Write the standard form of a circle with radius [latex]2[/latex] and center [latex](-1,3)[/latex].
Example 3: finding the center and radius
Find the center and radius, then graph the circle: [latex]{\left(x+2\right)}^{2}+{\left(y-1\right)}^{2}=9[/latex].
Use the standard form of a circle.
[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]
Identify the center [latex](h,k)[/latex], and radius [latex]r[/latex].
[latex]{\left(x-(-2)\right)}^{2}+{\left(y-1\right)}^{2}=3^{2}[/latex]
The center is [latex](-2,1)[/latex], and the radius is [latex]3[/latex].
Now graph the circle. Plot the center first and then go up, down, left, and right 2 places.

Example 4: finding the center and radius
Find the center and radius, then graph the circle: [latex]{4x}^{2}+{4y}^{2}=64[/latex].
GENERAL FORM OF A CIRCLE
The general form of a circle is as follows:
[latex]{x}^{2}+{y}^{2}+ax+by+c=0[/latex]
Example 5: WRITE THE STANDARD FORM Equation OF A CIRCLE
Find the center and radius, then graph: [latex]{x}^{2}+{y}^{2}-4x-6y+4=0[/latex].
We need to rewrite this general form into standard form in order to find the center and radius.
[latex]{x}^{2}+{y}^{2}-4x-6y+4=0[/latex]
Group the x-terms and y-terms. Collect the constants on the right right side.
[latex]{x}^{2}-4x+{y}^{2}-6y=-4[/latex]
Complete the squares.
[latex]{x}^{2}-4x+4+{y}^{2}-6y+9=-4+4+9[/latex]
Rewrite as binomial squares.
[latex]{\left(x-2\right)}^{2}+{\left(y-3\right)}^{2}=9[/latex]
The center is [latex](2,3)[/latex], and the radius is [latex]3[/latex].
Now graph the circle. Plot the center first and then go up, down, left, and right 3 places.

Example 6: WRITE THE STANDARD FORM Equation OF A CIRCLE
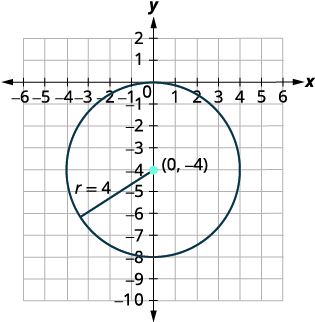
Find the center and radius, then graph: [latex]{x}^{2}+{y}^{2}+8y=0[/latex].
Example 7: APPLYING THE DISTANCE AND MIDPOINT FORMULAS TO A CIRCLE EQUATION
The diameter of a circle has endpoints [latex](-1,-4)[/latex] and [latex](7,2)[/latex]. Find the center and radius of the circle and also write its standard form equation.
The center of a circle is the center, or midpoint, of its diameter. Thus the midpoint formula will yield the center point.
[latex]M=\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)[/latex]
[latex]=\left(\frac{-1+7}{2},\frac{-4+2}{2}\right)[/latex]
[latex]=\left(\frac{6}{2},\frac{-2}{2}\right)[/latex]
[latex]=(3,-1)[/latex]
The center is [latex](3,-1)[/latex]. The distance formula will be used to find the distance from the center to one of the points on the circle. This will yield the radius:
[latex]d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}[/latex]
[latex]d=\sqrt{(7-3)^{2}+(2-(-1))^{2}}[/latex]
[latex]d=\sqrt{4^{2}+3^{2}}=5[/latex]
The distance from the center to a point on the circle is 5. Therefore the radius is 5. The center and radius can now be used to find the standard form of the circle:
Start with the standard form of a circle.
[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]
Substitute in the values [latex]r=5, h=3, k=-1[/latex].
[latex]{\left(x-3\right)}^{2}+{\left(y-(-1)\right)}^{2}=5^{2}[/latex]
Simplify.
[latex]{\left(x-3\right)}^{2}+{\left(y+1\right)}^{2}=25[/latex]
Example 8: Finding the Center of a Circle
The diameter of a circle has endpoints [latex]\left(-1,-4\right)[/latex] and [latex]\left(5,-4\right)[/latex]. Find the center of the circle.
Key Concepts
- A circle is all points in a plane that are a fixed distance from a given point on the plane. The given point is called the center, and the fixed distance is called the radius.
- The standard form of the equation of a circle with center [latex](h,k)[/latex] and radius [latex]r[/latex] is [latex]{\left(x-h\right)}^{2}{+}{\left(y-k\right)}^{2}=r^{2}[/latex]
Section 1.2 Homework Exercises
For the following exercises, write the standard form of the equation of the circle with the given radius and center [latex](0,0)[/latex].
1. Radius: [latex]7[/latex]
2. Radius: [latex]9[/latex]
3. Radius: [latex]\sqrt{2}[/latex]
4. Radius: [latex]\sqrt{5}[/latex]
In the following exercises, write the standard form of the equation of the circle with the given radius and center.
5. Radius: [latex]1[/latex], center: [latex](3,5)[/latex]
6. Radius: [latex]10[/latex], center: [latex](-2,6)[/latex]
7. Radius: [latex]2.5[/latex], center: [latex](1.5,-3.5)[/latex]
8. Radius: [latex]1.5[/latex], center: [latex](-5.5,-6.5)[/latex]
For the following exercises, write the standard form of the equation of the circle with the given center and point on the circle.
9. Center: [latex](3,-2)[/latex] with point [latex](3,6)[/latex]
10. Center: [latex](6,-6)[/latex] with point [latex](2,-3)[/latex]
11. Center: [latex](4,4)[/latex] with point [latex](2,2)[/latex]
12. Center: [latex](-5,6)[/latex] with point [latex](-2,3)[/latex]
In the following exercises, find the center and radius and then graph each circle.
13. [latex]{\left(x+5\right)}^{2}+{\left(y+3\right)}^{2}=1[/latex]
14. [latex]{\left(x-2\right)}^{2}+{\left(y-3\right)}^{2}=9[/latex]
15. [latex]{\left(x-4\right)}^{2}+{\left(y+2\right)}^{2}=16[/latex]
16. [latex]{\left(x+2\right)}^{2}+{\left(y-5\right)}^{2}=4[/latex]
17. [latex]x^{2}+{\left(y+2\right)}^{2}=25[/latex]
18. [latex]{\left(x-1\right)}^{2}+{y}^{2}=36[/latex]
19. [latex]{\left(x-1.5\right)}^{2}+{\left(y-2.5\right)}^{2}=0.25[/latex]
20. [latex]{\left(x-1\right)}^{2}+{\left(y-3\right)}^{2}=\frac{9}{4}[/latex]
21. [latex]x^{2}+y^{2}=64[/latex]
22. [latex]x^{2}+y^{2}=49[/latex]
23. [latex]2x^{2}+2y^{2}=8[/latex]
24. [latex]6x^{2}+6y^{2}=216[/latex]
In the following exercises, identify the center and radius and graph.
25. [latex]x^{2}+y^{2}+2x+6y+9=0[/latex]
26. [latex]x^{2}+y^{2}-6x-8y=0[/latex]
27. [latex]x^{2}+y^{2}-4x+10y-7=0[/latex]
28. [latex]x^{2}+y^{2}+12x-14y+21=0[/latex]
29. [latex]x^{2}+y^{2}+6y+5=0[/latex]
30. [latex]x^{2}+y^{2}-10y=0[/latex]
31. [latex]x^{2}+y^{2}+4x=0[/latex]
32. [latex]x^{2}+y^{2}-14x+13=0[/latex]
33. Explain the relationship between the distance formula and the equation of a circle.
34. In your own words, state the definition of a circle.
35. In your own words, explain the steps you would take to change the general form of the equation of a circle to the standard form.