7.1 Composing Functions

Learning Outcomes

  • Evaluate composite functions.
  • Find composite functions.

Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. Notice how we have just defined two relationships: The cost depends on the temperature, and the temperature depends on the day.

Explanation of C(T(5)), which is the cost for the temperature and T(5) is the temperature on day 5.

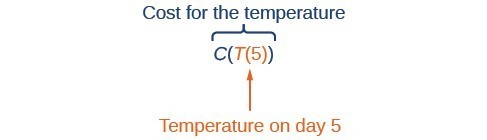
Using descriptive variables, we can notate these two functions. The function [latex]C\left(T\right)[/latex] gives the cost [latex]C[/latex] of heating a house for a given average daily temperature in [latex]T[/latex] degrees Celsius. The function [latex]T\left(d\right)[/latex] gives the average daily temperature on day [latex]d[/latex] of the year. For any given day, [latex]\text{Cost}=C\left(T\left(d\right)\right)[/latex] means that the cost depends on the temperature which in turns depends on the day of the year. Thus, we can evaluate the cost function at the temperature [latex]T\left(d\right)[/latex]. For example, we could evaluate [latex]T\left(5\right)[/latex] to determine the average daily temperature on the [latex]5[/latex]th day of the year. Then, we could evaluate the cost function at that temperature. We would write [latex]C\left(T\left(5\right)\right)[/latex]. By combining these two relationships into one function, we have performed function composition.

Composition of Functions

The composite function [latex]f \circ g[/latex], the composition of [latex]f[/latex] and [latex]g[/latex], is defined as [latex](f \circ g)(x) \ =\ f(g(x))[/latex]

We read the left-hand side as [latex]"f[/latex] composed with [latex]g[/latex] at [latex]x,"[/latex] and the right-hand side as [latex]"f[/latex] of [latex]g[/latex] of [latex]x."[/latex] The open circle symbol [latex]\circ[/latex] is called the composition operator.

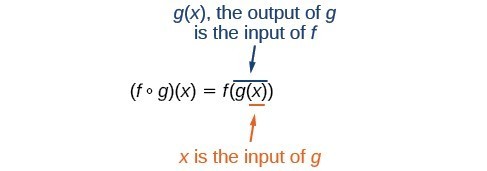
the composition f composed with g at x is f of g of x. g(x), the output of g is the input of f. x is the input of g.
It is important to correctly apply the order of operations when evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first and then working to the outside.

Once we compose a new function from two existing functions, we need to be able to evaluate it for any input in its domain. We will do this with specific numerical inputs for functions expressed as tables, graphs, and formulas and with variables as inputs to functions expressed as formulas. In each case we evaluate the inner function using the starting input and then use the inner function’s output as the input for the outer function.

Evaluating Composite Functions Using Formulas

EXAMPLE

Given [latex]f\left(x\right)=-3x-2[/latex] and [latex]g\left(x\right)=x+5[/latex], evaluate [latex]\left( f \circ g \right)[/latex] for [latex]x=2[/latex].

[latex]\left( f \circ g \right)\left(2\right) = f\left(g\left(2\right)\right)[/latex].

Example

Given [latex]f\left(x\right)=2x+1[/latex] and [latex]g\left(x\right)=3-x[/latex], find [latex]f\left(g\left(x\right)\right)[/latex] and [latex]g\left(f\left(x\right)\right)[/latex].

 

In the following video, you will see another example of how to find the composition of two functions.

 

EXAMPLE

Given [latex]f\left(x\right)=4x+3[/latex] and [latex]g\left(x\right)=4x^2+3x-1[/latex], find [latex]\left(f\circ g\right)[/latex] and [latex]\left(g\circ f\right)[/latex].

 

Evaluating Composite Functions Using Tables

When working with functions given as tables, we read input and output values from the table entries and always work from the inside to the outside. We evaluate the inside function first and then use the output of the inside function as the input to the outside function.

Example: Using a Table to Evaluate a Composite Function

Using the table below, evaluate [latex]f\left(g\left(3\right)\right)[/latex] and [latex]g\left(f\left(3\right)\right)[/latex].

[latex]x[/latex] [latex]f\left(x\right)[/latex] [latex]g\left(x\right)[/latex]
1 6 3
2 8 5
3 3 2
4 1 7

Try It

Using the table below, evaluate [latex]f\left(g\left(1\right)\right)[/latex] and [latex]g\left(f\left(4\right)\right)[/latex].

[latex]x[/latex] [latex]f\left(x\right)[/latex] [latex]g\left(x\right)[/latex]
1 6 3
2 8 5
3 3 2
4 1 7

Try It

Practice using the table to evaluate the functions below.

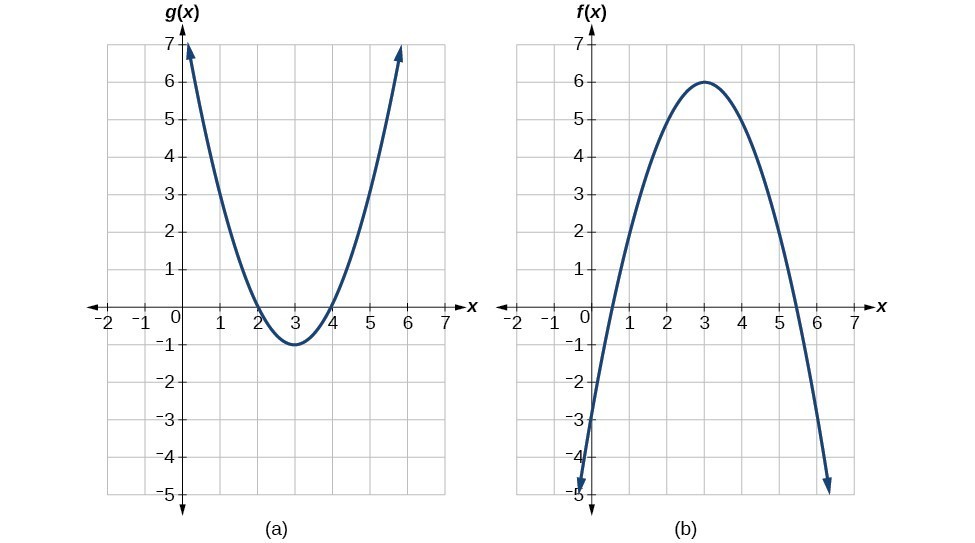
Evaluating Composite Functions Using Graphs

Given individual functions as graphs, evaluation of composite functions is similar to evaluation using tables, but the input and output values are found from the [latex]x\text{-}[/latex] and [latex]y\text{-}[/latex] axes of the graphs.

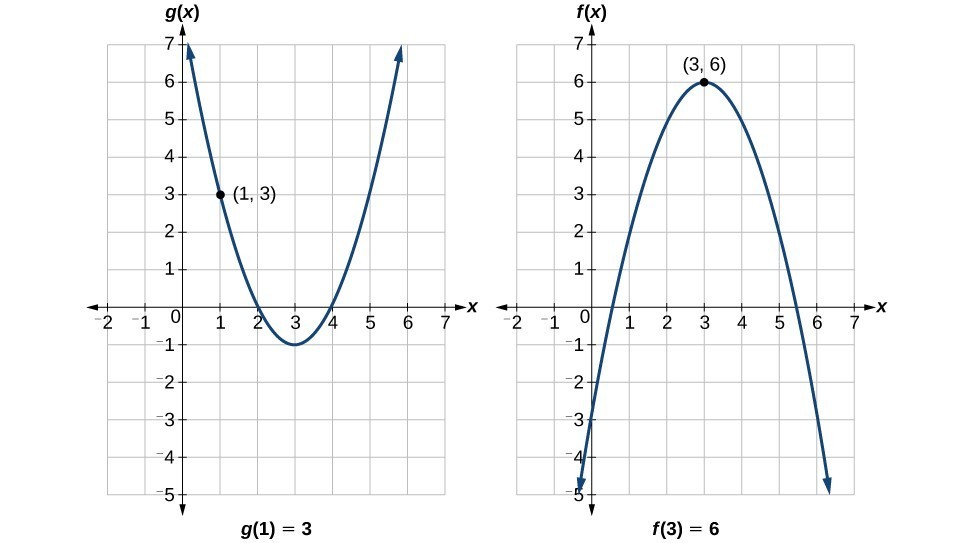
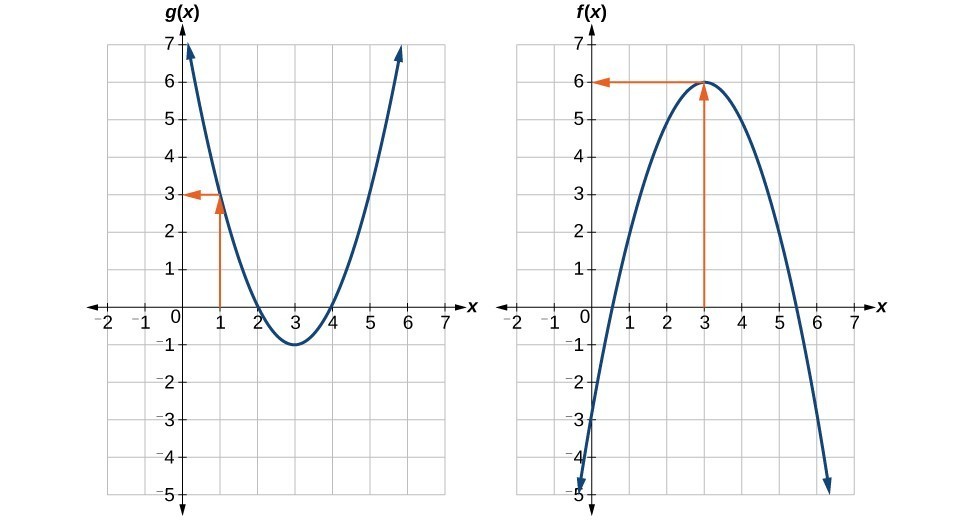
Example: Using a Graph to Evaluate a Composite Function

Using the graphs below, evaluate [latex]f\left(g\left(1\right)\right)[/latex].

Explanation of the composite function.