One-to-One Functions

Recall that in a function, the input value must have one and only one value for the output. The set of input values is the domain of the function and the set of output values is the range of the function.

Some functions have a given output value that corresponds to two or more input values. For example, in the following stock chart the stock price was [latex]$1000[/latex] on five different dates, meaning that there were five different input values that all resulted in the same output value of [latex]$1000[/latex].

However, some functions have only one input value for each output value as well as having only one output value for each input value. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents as listed below.

This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.

To visualize this concept, look at the two simple functions sketched in (a) and (b) below. Note that (c) is not a function since the input q produces two outputs, y and z.

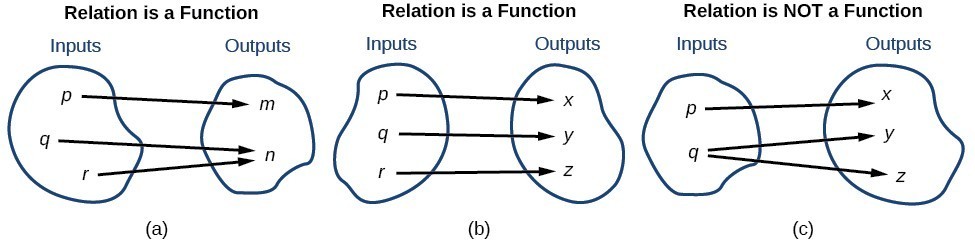
The function in part (a) shows a relationship that is not a one-to-one function because inputs [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.

In the following video, we show an example of using tables of values to determine whether a function is one-to-one.

Using the Horizontal Line Test

An easy way to determine whether a function is a one-to-one function is to use the horizontal line test on the graph of the function.  To do this, draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.

EXAMPLE

For the following graphs, determine which represent one-to-one functions.

Show Solution

The function in (a) is not one-to-one. Using the horizontal line test, as shown below, it intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)

The function in (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.

 

The function (c) is not one-to-one and is in fact not a function.

 

The following video provides another example of using the horizontal line test to determine whether a graph represents a one-to-one function.

Inverse Functions

Given a one-to-one function [latex]f\left(x\right)[/latex], we represent its inverse as [latex]{f}^{-1}\left(x\right)[/latex], read as “[latex]f[/latex] inverse of [latex]x[/latex].” The superscript [latex]-1[/latex] is part of the notation. It is not an exponent; it does not imply a power of [latex]-1[/latex] . In other words, [latex]{f}^{-1}\left(x\right)[/latex] does not mean [latex]\dfrac{1}{f\left(x\right)}[/latex]. Instead, [latex]\dfrac{1}{f\left(x\right)}[/latex] is the reciprocal of [latex]f[/latex], not the inverse.

Why -1?

The “exponent-like” notation comes from an analogy between function composition and multiplication: just as [latex]{a}^{-1}a=1[/latex] for any nonzero number [latex]a[/latex], so [latex]\left({f}^{-1}\circ f\right)\left(x\right)={f}^{-1}\left(f\left(x\right)\right)={f}^{-1}\left(y\right)=x[/latex]. This is true for all [latex]x[/latex] in the domain of [latex]f[/latex]. Informally, this means that inverse functions “undo” each other. However, just as zero does not have a reciprocal, some functions do not have inverses.

Verify that Functions are Inverses

Given a function [latex]f\left(x\right)[/latex], we can verify whether some other function [latex]g\left(x\right)[/latex] is the inverse of [latex]f\left(x\right)[/latex] by checking whether both [latex]g\left(f\left(x\right)\right)=x[/latex] and [latex]f\left(g\left(x\right)\right)=x[/latex].

For example, [latex]y=4x[/latex] and [latex]y=\dfrac{1}{4}x[/latex] are inverse functions.

[latex]\left({f}^{-1}\circ f\right)\left(x\right)={f}^{-1}\left(f\left(x\right)\right)={f}^{-1}\left(4x\right)=\dfrac{1}{4}\left(4x\right)=x[/latex]

and

[latex]\left({f}^{}\circ {f}^{-1}\right)\left(x\right)=f\left({f}^{-1}\left(x\right)\right)=f\left(\dfrac{1}{4}x\right)=4\left(\dfrac{1}{4}x\right)=x[/latex]

These videos have more examples of algebraically verifying if two functions are inverse functions.

Finding Inverses of Linear Functions

If we have a linear function given as a formula—for example, [latex]y[/latex] as a function of [latex]x[/latex]—we can find the inverse function by solving to obtain [latex]x[/latex] as a function of [latex]y[/latex].

This video demonstrates finding the inverse of a linear function.

Graph a Linear Function and its Inverse

To graph the inverse of a linear function, one approach is to find two or more points on the graph of the linear function. Then simply switch the [latex]x[/latex]– and [latex]y[/latex]-coordinates of each point to find points that lie on the graph of the inverse function. Then use these points to graph the inverse function. For example, [latex] (0, 0) [/latex] and [latex] (1, 2) [/latex] are two points that lie on the graph of the function [latex]f(x)=2x[/latex]. To graph the inverse function, switch the [latex]x[/latex]– and [latex]y[/latex]-coordinates of these points to get [latex] (0, 0) [/latex] and [latex] (2, 1) [/latex]. The graph of the inverse function will be the line that passes through the two points [latex] (0, 0) [/latex] and [latex] (2, 1) [/latex] (See below).

Graph of the function [latex]f(x)=2x[/latex] and its inverse.

Example

Use the graph of the linear function [latex]f(x)=4x-2[/latex] to graph the inverse function.

 

Graph of [latex]f(x)=4x-2[/latex]

Show Answer

Choose 2 (or more) points on the original line: [latex] (0, –2) [/latex] and [latex] (1, 2) [/latex].To graph the inverse linear function, reverse the [latex]x[/latex]– and [latex]y[/latex]-coordinates: [latex] (–2, 0) [/latex] and [latex] (2, 1) [/latex].Plot the new points. The line that passes through them is the graph of the inverse function.

Graph of [latex]f(x)=4x-2[/latex] and its inverse

Try It

Use the graphs of the linear functions to graph their inverse functions.

1. Graph of [latex]f(x)=-3x+5[/latex]

1. Graph of [latex]f(x)=\frac{4}{3}x+2[/latex]

Show Answer

1. Graph of [latex]f(x)=-3x+5[/latex] and its inverse

2. Graph of [latex]f(x)=\frac{4}{3}x+2[/latex] and its inverse

Example

Find the inverse of the function [latex]f(x)=\frac{2}{5}x+2[/latex], then graph the function and its inverse.

Show Answer

First find the inverse function.

[latex]\require{color}\begin{align} f\left(x\right) &= \frac{2}{5}x+2&& \color{blue}{\textsf{write with $y$}}\\[5pt] y &= \frac{2}{5}x+2&& \color{blue}{\textsf{interchange $x$ and $y$}}\\[5pt] x &= \frac{2}{5}y+2&& \color{blue}{\textsf{multiply both sides of the equation by $5$}}\\[5pt] 5\left(x\right) &= 5\left(\frac{2}{5}y+2\right)&& \color{blue}{\textsf{solve for $y$}}\\[5pt] 5x &= 2y+10\\[5pt] 5x-10 &= 2y\\[5pt] \frac{5x-10}{2}&=y\\[5pt] y &= \frac{5}{2}x-5&& \color{blue}{\textsf{rename the function ${f}^{-1}\left(x\right)$}}\\[5pt] {f}^{-1}\left(x\right)&= \frac{5}{2}x-5\\[5pt] \end{align}[/latex]

 

Next, graph the function and its inverse. To graph [latex]f(x)=\frac{2}{5}x+2[/latex] we can either use a table of values or use the slope and [latex]y[/latex]-intercept.

The slope of the line is [latex]m=\frac{2}{5}[/latex] and the [latex]y[/latex]-intercept is [latex] (0, 2) [/latex].

To graph the line, we start at [latex] (0, 2) [/latex] then run [latex] 5 [/latex] units to the right and [latex] 2 [/latex] units up to get to [latex] (5, 4) [/latex].

Graph of [latex]f(x)=\frac{2}{5}x+2[/latex]

To graph [latex]f^{-1}\left(x\right)=\frac{5}{2}x-5[/latex] we can use a table of values, use the slope and [latex]y[/latex]-intercept, or reverse some of the points from [latex]f(x)[/latex].Let’s use the slope and intercept again. The slope of the line is [latex]m=\frac{5}{2}[/latex] and the [latex]y[/latex]-intercept is [latex] (0, -5) [/latex].To graph the line, we start at [latex] (0, -5) [/latex] then run [latex] 2 [/latex] units to the right and [latex] 5 [/latex] units up to get to [latex] (2,0) [/latex].

Graph of [latex]f(x)=\frac{2}{5}x+2[/latex] and its inverse [latex]f^{-1}(x)=\frac{5}{2}x-5[/latex]

Notice that if we instead reversed the points [latex] (0, 2) [/latex] and [latex] (5, 4) [/latex] from [latex] f(x) [/latex] to [latex] (2, 0) [/latex] and [latex] (4, 5) [/latex], we could draw the same line to graph the inverse function through these new points.Notice the relationship of the slope of the original function to the slope of the inverse function. The original function has a slope of [latex] \frac{2}{5} [/latex], while the inverse function has a slope of [latex]\frac{5}{2}[/latex]. i.e. the slopes are reciprocals of each other, but NOT negative reciprocals like perpendicular lines.

Inverse Functions and Symmetry

The graph of any function and its inverse are symmetric across the line [latex]y=x[/latex].  For example, the graph below shows the graph of [latex]f(x)=\frac{2}{5}x+2[/latex] and its inverse, [latex]f^{-1}(x)=\frac{5}{2}x-5[/latex]. Adding the dashed line [latex]y=x[/latex], we can see that the two lines are symmetric (mirror images of one another) across the line [latex]y=x[/latex].

Graph of [latex]f(x)=\frac{2}{5}x+2[/latex] and its inverse [latex]f^{-1}(x)=\frac{5}{2}x-5[/latex]

Notice the [latex]x[/latex]– and [latex]y[/latex]-intercepts. The [latex]y[/latex]-intercept of [latex] (0, 2) [/latex] in the original function (blue line) reflects to the [latex]x[/latex]-intercept [latex] (2, 0) [/latex] in the inverse function (green line). Also, the [latex]x[/latex]-intercept of [latex] (–5, 0) [/latex] in the original function (blue line) reflects to the [latex]y[/latex]-intercept [latex] (0, –5) [/latex] in the inverse function (green line).

The slopes of each function are also related. The function [latex]f(x)[/latex] has a slope of [latex]\frac{2}{5}[/latex], while the inverse function [latex]f^{-1}(x)[/latex] has a slope of [latex]\frac{5}{2}[/latex]. The slopes of inverse functions are reciprocals of each other. This is because the slope of a function is [latex]\dfrac{\text{change in y}}{\text{change in x}}[/latex]. The slope of the inverse function becomes [latex]\dfrac{\text{change in x}}{\text{change in y}}[/latex].