Learning Outcomes
- Evaluate exponential functions.
- Graph exponential functions by creating a table of values.
- Find the equation of the asymptote of an exponential function.
- Find the domain and the range of an exponential function using its graph and write them in interval notation.
Linear functions have a constant rate of change – a constant number that the output increases for each increase in input. For example, in the equation [latex]f(x)=3x+4[/latex] , the slope tells us the output increases by three each time the input increases by one. Sometimes, on the other hand, quantities grow by a percent rate of change rather than by a fixed amount. In this lesson, we will define a function whose rate of change increases by a percent of the current value rather than a fixed quantity.
To illustrate this difference consider two companies whose business is expanding: Company A has [latex]100[/latex] stores and expands by opening [latex]50[/latex] new stores a year, while Company B has [latex]100[/latex] stores and expands by increasing the number of stores by [latex]50\%[/latex] of their total each year.
The table below compares the growth of each company where company A increases the number of stores linearly, and company B increases the number of stores by a rate of [latex]50\%[/latex] each year.
| Year | Stores, Company A | Description of Growth | Stores, Company B |
| [latex]0[/latex] | [latex]100[/latex] | Starting with [latex]100[/latex] each | [latex]100[/latex] |
| [latex]1[/latex] | [latex]100+50=150[/latex] | They both grow by [latex]50[/latex] stores in the first year. | [latex]100[/latex][latex]+50\%[/latex] of [latex]100[/latex] [latex]100 + 0.50(100) = 150[/latex] |
| [latex]2[/latex] | [latex]150+50=200[/latex] | Store A grows by [latex]50[/latex], Store B grows by [latex]75[/latex] | [latex]150[/latex][latex]+ 50\%[/latex] of [latex]150[/latex] [latex]150 + 0.50(150) = 225[/latex] |
| [latex]3[/latex] | [latex]200+50=250[/latex] | Store A grows by [latex]50[/latex], Store B grows by [latex]112.5[/latex] | [latex]225 + 50\%[/latex] of [latex]225[/latex] [latex]225 + 0.50(225) = 337.5[/latex] |
Company A has [latex]100[/latex] stores and expands by opening [latex]50[/latex] new stores a year, so its growth can be represented by the function [latex]A\left(x\right)=100+50x[/latex]. Company B has [latex]100[/latex] stores and expands by increasing the number of stores by [latex]50\%[/latex] each year, so its growth can be represented by the function [latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex].
The graphs comparing the number of stores for each company over a five-year period are shown below. We can see that, with exponential growth, the number of stores increases much more rapidly than with linear growth.
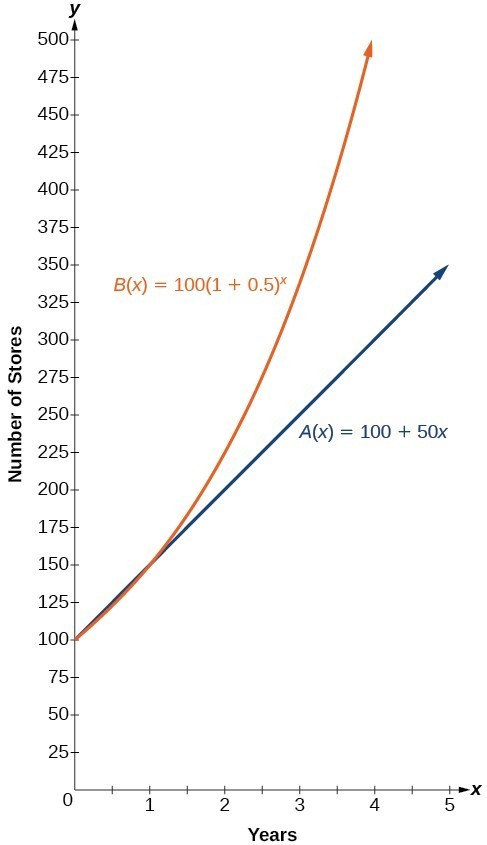
The graph shows the number of stores Companies A and B opened over a five-year period.
Notice that the domain for both functions is [latex]\left[0,\infty \right)[/latex], and the range for both functions is [latex]\left[100,\infty \right)[/latex]. After year [latex]1[/latex], Company B always has more stores than Company A.
Consider the function representing the number of stores for Company B:
[latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex]
In this exponential function, [latex]100[/latex] represents the initial number of stores, [latex]0.50[/latex] represents the growth rate, and [latex]1+0.5=1.5[/latex] represents the growth factor. Generalizing further, we can write this function as [latex]B\left(x\right)=100{\left(1.5\right)}^{x}[/latex], where [latex]100[/latex] is the initial value, [latex]1.5[/latex] is called the base, and x is called the exponent. This is an exponential function.
Exponential Growth
A function that models exponential growth grows by a rate proportional to the current amount. For any real number x and any positive real numbers a and b such that [latex]b\ne 1[/latex], an exponential growth function has the form
where
- a is the initial or starting value of the function.
- b is the growth factor or growth multiplier per unit x.
To evaluate an exponential function of the form [latex]f\left(x\right)={b}^{x}[/latex], we simply substitute x with the given value, and calculate the resulting power. For example:
Let [latex]f\left(x\right)={2}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?
To evaluate an exponential function with a form other than the basic form, it is important to follow the order of operations. For example:
Let [latex]f\left(x\right)=30{\left(2\right)}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?
Note that if the order of operations were not followed, the result would be incorrect:
Example
Let [latex]f\left(x\right)=5{\left(3\right)}^{x+1}[/latex]. Evaluate [latex]f\left(2\right)[/latex] without using a calculator.
In the following video, we present more examples of evaluating an exponential function at several different values.
In the next example, we will revisit the population of India.
Example
At the beginning of this section, we learned that the population of India was about [latex]1.25[/latex] billion in the year [latex]2013[/latex], with an annual growth rate of about [latex]1.2\%[/latex]. This situation is represented by the growth function [latex]P\left(t\right)=1.25{\left(1.012\right)}^{t}[/latex], where t is the number of years since [latex]2013[/latex]. To the nearest thousandth, what will the population of India be in [latex]2031[/latex]?
In the following video, we show another example of using an exponential function to predict the population of a small town.
Summary
Exponential growth grows by a rate proportional to the current amount. For any real number x and any positive real numbers a and b such that [latex]b\ne 1[/latex], an exponential growth function has the form [latex]f\left(x\right)=a{b}^{x}[/latex]. Evaluating exponential functions requires careful attention to the order of operations. Compound interest is an example of exponential growth.
We learn a lot about things by seeing their pictorial representations, and that is exactly why graphing exponential equations is a powerful tool. It gives us another layer of insight for predicting future events. Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is greater than one. We will use the function [latex]f\left(x\right)={2}^{x}[/latex]. Observe how the output values in the table below change as the input increases by [latex]1[/latex].
| x | [latex]–3[/latex] | [latex]–2[/latex] | [latex]–1[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] |
| [latex]f\left(x\right)={2}^{x}[/latex] | [latex]\frac{1}{8}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{2}[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]4[/latex] | [latex]8[/latex] |
Each output value is the product of the previous output and the base, [latex]2[/latex]. We call the base [latex]2[/latex] the constant ratio. In fact, for any exponential function of the form [latex]f\left(x\right)=a{b}^{x}[/latex], b is the constant ratio of the function. This means that as the input increases by [latex]1[/latex], the output value will be the product of the base and the previous output, regardless of the value of a.
Notice from the table that
- the output values are positive for all values of x;
- as x increases, the output values increase without bound; and
- as x decreases, the output values grow smaller, approaching zero.
The graph below shows the exponential growth function [latex]f\left(x\right)={2}^{x}[/latex].
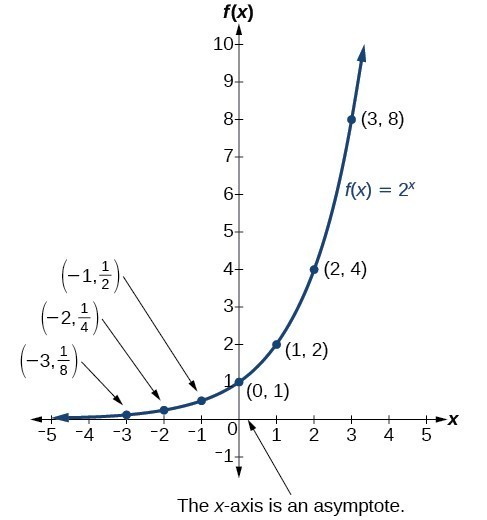
In the graph, notice that the graph gets close to the x-axis, but never touches it.
The domain of [latex]f\left(x\right)={2}^{x}[/latex] is all real numbers; the range is [latex]\left(0,\infty \right)[/latex].
To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is between zero and one. We will use the function [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex]. Observe how the output values in the table below change as the input increases by [latex]1[/latex].
| x | –[latex]3[/latex] | –[latex]2[/latex] | –[latex]1[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] |
| [latex]g\left(x\right)=\left(\frac{1}{2}\right)^{x}[/latex] | [latex]8[/latex] | [latex]4[/latex] | [latex]2[/latex] | [latex]1[/latex] | [latex]\frac{1}{2}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{8}[/latex] |
Again, because the input is increasing by [latex]1[/latex], each output value is the product of the previous output and the base, or constant ratio [latex]\frac{1}{2}[/latex].
Notice from the table that:
- the output values are positive for all values of x;
- as x increases, the output values grow smaller, approaching zero; and
- as x decreases, the output values grow without bound.
The graph shows the exponential decay function, [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex].
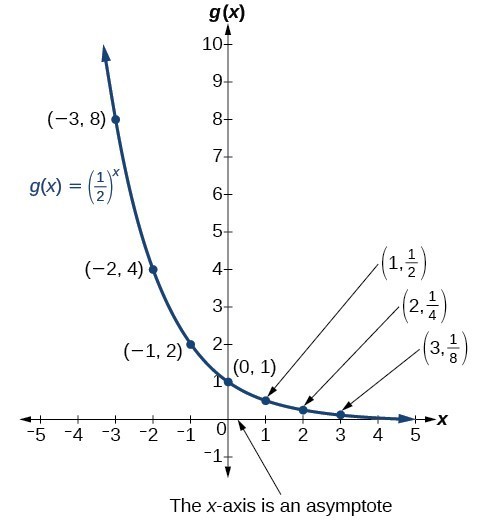
The domain of [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex] is all real numbers; the range is [latex]\left(0,\infty \right)[/latex].
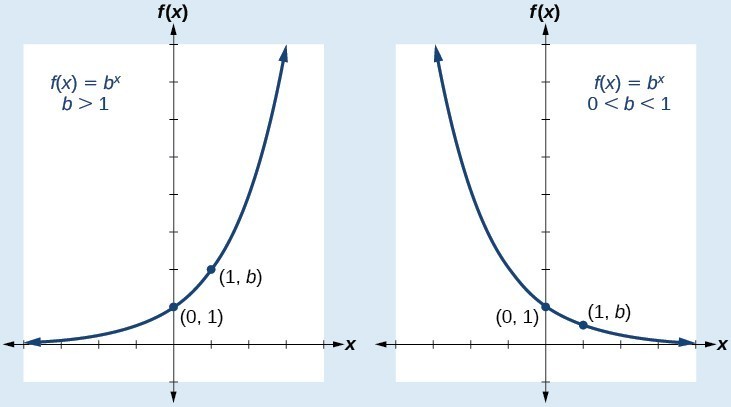
Characteristics of the Graph of [latex]f(x) = b^{x}[/latex]
An exponential function of the form [latex]f\left(x\right)={b}^{x}[/latex], [latex]b>0[/latex], [latex]b\ne 1[/latex], has these characteristics:
- one-to-one function
- domain: [latex]\left(-\infty , \infty \right)[/latex]
- range: [latex]\left(0,\infty \right)[/latex]
- x-intercept: none
- y-intercept: [latex]\left(0,1\right)[/latex]
- increasing if [latex]b>1[/latex]
- decreasing if [latex]b<1[/latex]
Compare the graphs of exponential growth and decay functions below.
In our first example, we will plot an exponential decay function where the base is between 0 and 1.
Example
Sketch a graph of [latex]f\left(x\right)={0.25}^{x}[/latex]. State the domain, range.
In the following video, we show another example of graphing an exponential function. The base of the exponential term is between [latex]0[/latex] and [latex]1[/latex], so this graph will represent decay.
How To: Given an exponential function of the form [latex]f\left(x\right)={b}^{x}[/latex], graph the function
- Create a table of points.
- Plot at least [latex]3[/latex] point from the table, including the y-intercept [latex]\left(0,1\right)[/latex].
- Draw a smooth curve through the points.
- State the domain, [latex]\left(-\infty ,\infty \right)[/latex], and the range, [latex]\left(0,\infty \right)[/latex].
In our next example, we will plot an exponential growth function where the base is greater than [latex]1[/latex].
Example
Sketch a graph of [latex]f(x)={\sqrt{2}(\sqrt{2})}^{x}[/latex]. State the domain and range.
Our next video example includes graphing an exponential growth function and defining the domain and range of the function.
Summary
Graphs of exponential growth functions will have a right tail that increases without bound and a left tail that gets really close to the x-axis. On the other hand, graphs of exponential decay functions will have a left tail that increases without bound and a right tail that gets really close to the x-axis. Points can be generated with a table of values which can then be used to graph the function.
