Why explain the use of graphs and create graphs using linear equations?
Much as the road sign at the right can help you quickly understand a “falling rocks” hazard ahead, graphs are a useful way of conveying information visually. Graphs of linear equations are especially effective for representing relationships between things that change at a constant rate, and they often do a better job than words or mathematical equations alone.
Suppose your manager has asked you to create and present a financial report at the next company meeting. She wants to know how the amount of revenue your team brought to the company changed during the last year. Your job is to get the information and choose the best method for communicating it.
You start with a table and add the values:
| Month | Revenue |
|---|---|
| 0 | 1000 |
| 1 | 1250 |
| 3 | 1750 |
| 5 | 2250 |
| 7 | 2750 |
| 9 | 3250 |
| 11 | 3750 |
The table is nicely organized, and its values are very precise, but it doesn’t readily show how the values change over time. So you study the numbers and try to describe this change in words:
Our team started the year with $1000 per month in revenue. For each additional month in the year 2015, our team produced an increase in $250 of revenue.
Next, you try expressing the information as a linear equation: [latex]y=250x+1000[/latex]
Again, both are very accurate, but neither reading two sentences out loud nor putting an equation on a poster board will go over very well with your manager or team members. You haven’t given them a way to picture the information. So, you try graphing the equation, which gives you the following:
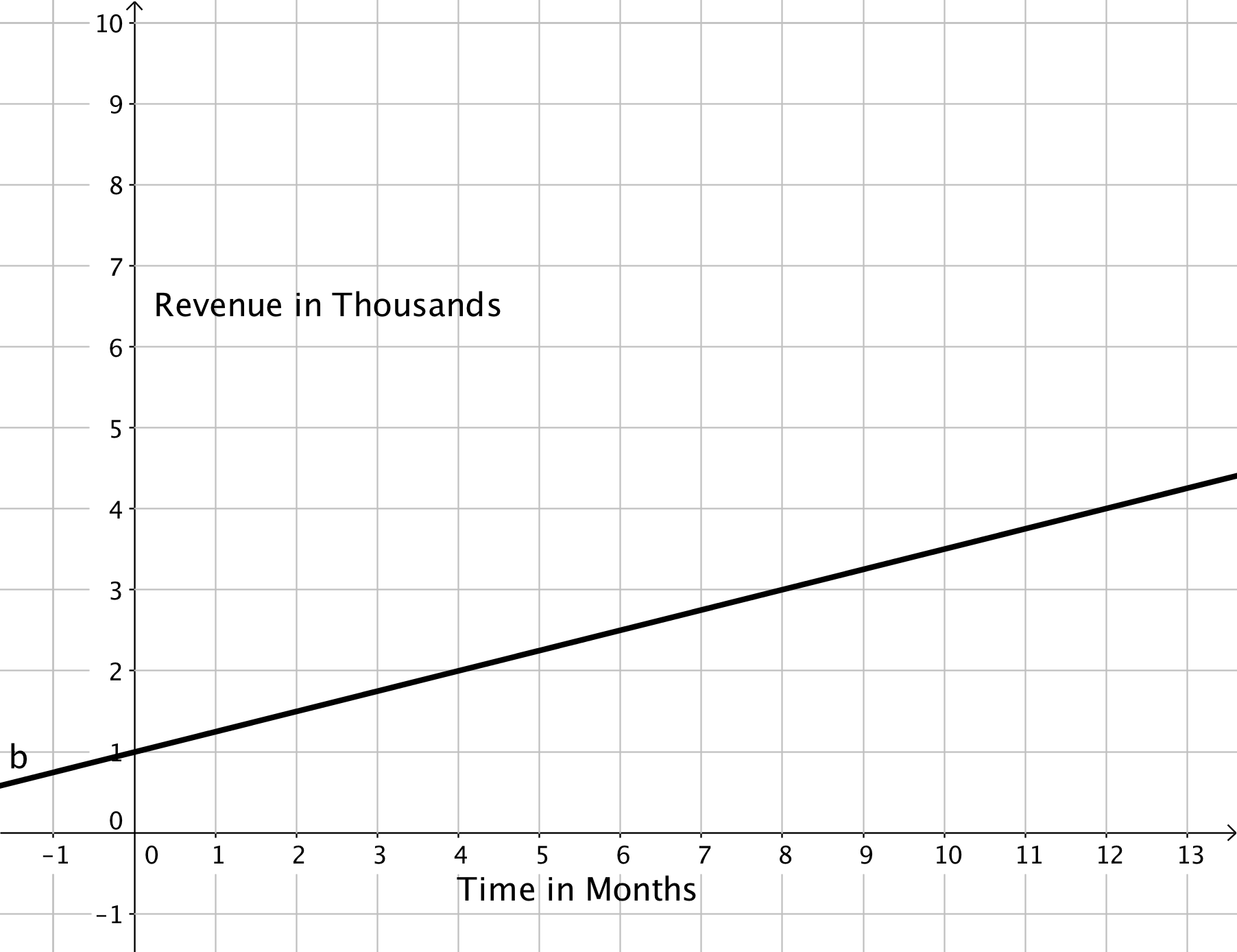
Graph showing the linear relationship between time and the change in revenue.
All four—the table, the words, the equation, and the graph—are representations of the same thing. And, depending on your purpose, one representation may get your point across more clearly than another. As you can see, graphs are especially good at conveying information about the relationship between things (in this case, time and revenue) with very little explanation. Your graph shows that the revenue your team produced during the last year steadily increased—a very encouraging trend! You decide that the graph is definitely what you’ll present at the meeting.
In this module, you’ll learn how to create Cartesian graphs (like the one above) and why graphs are an especially useful means of conveying information.
Learning Outcomes
- The Coordinate Plane
- Plot ordered pairs
- Identify quadrants on the coordinate plane
- Graphing Linear Equations
- Graph an equation using ordered pairs
- Graph linear equations in different forms
- Graph an equation using intercepts
- Slope
- Find the slope from a graph
- Find the slope from two points
- Find the slope of horizontal and vertical lines
- Equations of Lines
- Write the equation and draw the graph of a line using slope and y-intercept
- Write and solve equations of lines using slope and a point on the line
- Write and solve equations of lines using two points on the line
- Parallel and Perpendicular Lines
- Identify slopes of parallel and perpendicular lines
- Write equations of parallel and perpendicular lines
- Applications of Graphs
- Interpret slope in equations and graphs
- Interpret the y-intercept of a linear equation and use that equation to make predictions
- Graphing Linear Inequalities
- Classify solutions and graphs as equations or inequalities
- Graph an inequality in two variables