Why It Matters: Rational Expressions and Equations

Why study rational expressions and equations?

If you were around in 2011, you probably heard about Occupy Wall Street, the protest against social and economic inequality in the US. According to Wikipedia, the main issues raised by Occupy Wall Street were social and economic inequality, greed, corruption, and the perceived undue influence of corporations on government—particularly from the financial services sector. The OWS slogan, “We are the 99%”, refers to income inequality and wealth distribution in the U.S. between the wealthiest 1% and the rest of the population. To achieve their goals, protesters acted on consensus-based decisions made in general assemblies which emphasized direct action over petitioning authorities for redress.

The Wall Street bull sculpture with a dancer on top.

Occupy Wall Street Ad

Economists are also interested in how wealth is distributed in economies.  The Lorenz curve is a mathematical representation of the distribution of income or of wealth. Max O. Lorenz developed it in 1905 to represent inequality of the wealth distribution.

The curve in the graph below shows the proportion of overall income or wealth assumed by the bottom x% of the people. It is often used to represent income distribution, where it shows for the bottom x% of households, what percentage (y%) of the total income they have. The percentage of households is plotted on the x-axis, the percentage of income is on the y-axis. It can also be used to show distribution of assets. In such use, many economists consider it to be a measure of social inequality.

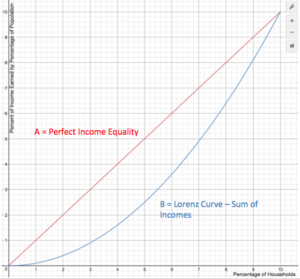
Graph with line of y=x and Lorenz curve that is concave up in relation to y=x. Lines are labeled A = perfect income equality with respect to y=x. B=Lorenz Curve - Sum of incomes.

Lorenz Curve

Points on the Lorenz curve represent statements like “the bottom 20% of all households have 10% of the total income.” A perfectly equal income distribution would be one in which every person has the same income. In this case, the bottom N% of society would always have N% of the income. This can be depicted by the straight line y = x; called the “line of perfect equality.”

By contrast, a perfectly unequal distribution would be one in which one person has all the income and everyone else has none. In that case, the curve would be at y = 0% for all x < 100%, and y = 100% when x = 100%. This curve is called the “line of perfect inequality.”

The Gini coefficient is the ratio of the area between the line of perfect equality and the observed Lorenz curve to the area between the line of perfect equality and the line of perfect inequality. The higher the coefficient, the more unequal the distribution is. This is given by the ratio [latex]G=\frac{A}{A+B}[/latex], where A and B are the areas of regions as marked in the graph below.

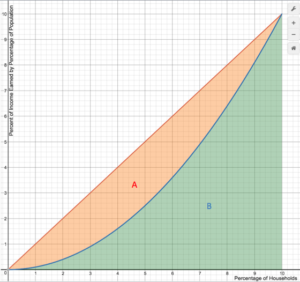
Graph of y=x and lorenz curve, shaded under y=x and shaded under the lorenz curve.

Gini Index

The closer the Gini index index is to 1, the less equally wealth is distributed amongst an economy.  The closer it is to 0, the more equally wealth is distributed. Below is a map of the world with Gini Index color coded.

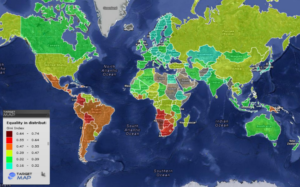
World map color coded by Gini Index

World map color coded by Gini Index

The Gini Index is a rational expression, or ratio. In this module, we will define and apply mathematical operations to rational expressions.  We will also solve rational equations.

Learning Outcomes

  • Operations With Rational Expressions
    • Define and simplify rational expressions
    • Multiply and divide rational expressions
    • Add and subtract rational expressions
  • Rational Equations
    • Solve rational equations
    • Solve proportional problems
    • Solve work equations
    • Solve variation problems