Lattice Energy and Enthalpy of Solution

The Born-Haber Cycle

It is not possible to measure lattice energies directly. However, the lattice energy can be calculated using the equation given in the previous section or by using a thermochemical cycle. The Born-Haber cycle is an application of Hess’s law that breaks down the formation of an ionic solid into a series of individual steps:

[latex]\Delta{H}_{\text{f}}^{\circ},[/latex] the standard enthalpy of formation of the compound
IE, the ionization energy of the metal
EA, the electron affinity of the nonmetal
[latex]\Delta{H}_{s}^{\circ},[/latex] the enthalpy of sublimation of the metal
D, the bond dissociation energy of the nonmetal
ΔH_lattice, the lattice energy of the compound

Figure 2 diagrams the Born-Haber cycle for the formation of solid cesium fluoride.

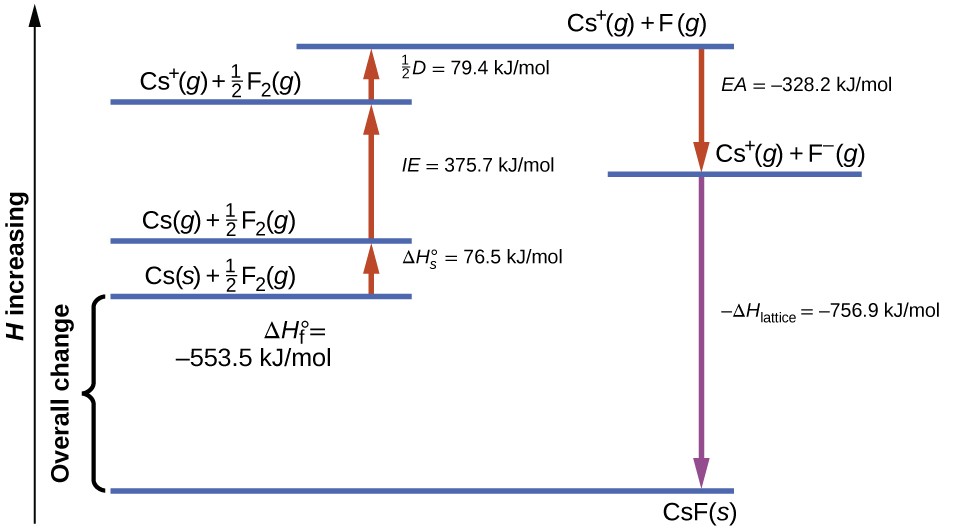
A diagram is shown. An upward facing arrow is drawn to the far left of the chart and is labeled “H increasing.” A horizontal line is drawn at the bottom of the chart. A downward-facing, vertical arrow to the left side of this line is labeled, “Overall change.” Beside this arrow is another label, “capital delta H subscript f, equals negative 553.5 k J per mol, ( Enthalpy of formation ).” Three horizontal lines, one above the other, and all above the bottom line, are labeled, from bottom to top, as: “C s ( s ), plus sign, one half F subscript 2, ( g ),” “C s ( g ), plus sign, one half F subscript 2, ( g ),” and “C s, superscript positive sign, ( g ), plus sign, one half F subscript 2, ( g ).” Each of these lines is connected by an upward-facing vertical arrow. Each arrow is labeled, “capital delta H subscript 1, equals 76.5 k J per mol, ( Enthalpy of sublimation ),” “capital delta H subscript 2, equals 375.7 k J per mol, ( ionization energy ),” and “capital delta H subscript 3 equals 79.4 k J / mol ( one half dissociation energy ).” Another horizontal line is drawn in the center top portion of the diagram and is labeled “C s, superscript positive sign, ( g ), plus sign, F, ( g ).” There is one more horizontal line drawn to the right of the overall diagram and located halfway down the image. An arrow connects the top line to this line and is labeled, “capital delta H equals negative 328.2 k J / mol ( electron affinity ).” The line is labeled, “C s superscript positive sign ( g ) plus F superscript negative sign ( g ).” The arrow connecting this line to the bottom line is labeled, “negative capital delta H subscript lattice equals negative 756.9 k J / mol.” The arrow points to a label on the bottom line which reads, “C s F ( s ).”

We begin with the elements in their most common states, Cs(s) and F₂(g). The [latex]\Delta{H}_{s}^{\circ}[/latex] represents the conversion of solid cesium into a gas, and then the ionization energy converts the gaseous cesium atoms into cations. In the next step, we account for the energy required to break the F-F bond to produce fluorine atoms. Converting one mole of fluorine atoms into fluoride ions is an exothermic process, so this step gives off energy (the electron affinity) and is shown as decreasing along the y-axis. We now have one mole of Cs cations and one mole of F anions. These ions combine to produce solid cesium fluoride. The enthalpy change in this step is the negative of the lattice energy, so it is also an exothermic quantity. The total energy involved in this conversion is equal to the experimentally determined enthalpy of formation, [latex]\Delta{H}_{\text{f}}^{\circ},[/latex] of the compound from its elements. In this case, the overall change is exothermic.

Hess’s law can also be used to show the relationship between the enthalpies of the individual steps and the enthalpy of formation. Table 3 shows this for cesium chloride, CsCl₂.

Table 3
Enthalpy of sublimation of Cs(s)	[latex]\text{Cs}\left(s\right)\rightarrow\text{Cs}\left(g\right)\Delta H=\Delta{H}_{s}^{\circ}=76.5\text{kJ}[/latex]
One-half of the bond energy of Cl₂	[latex]\frac{1}{2}{\text{Cl}}_{2}\text{(}g\text{)}\rightarrow\text{Cl}\left(g\right)\Delta H=\frac{1}{2}D=122\text{kJ}[/latex]
Ionization energy of Na(g)	[latex]\text{Na}\left(g\right)\rightarrow{\text{Na}}^{\text{+}}\text{(}g\text{)}+{\text{e}}^{-}\Delta H=IE=496\text{kJ}[/latex]
Negative of the electron affinity of Cl	[latex]\text{Cl}\left(g\right)+{\text{e}}^{-}\rightarrow{\text{Cl}}^{-}\text{(}g\text{)}\Delta H=-EA=-368\text{kJ}[/latex]
Negative of the lattice energy of NaCl(s)	[latex]{\text{Na}}^{\text{+}}\text{(}g\text{)}+{\text{Cl}}^{-}\text{(}g\text{)}\rightarrow\text{NaCl}\left(s\right)\Delta H=-{\Delta{H}}_{\text{lattice}}=?[/latex]
Enthalpy of formation of NaCl(s), add steps 1–5	[latex]\begin{array}{l}\Delta H=\Delta{H}_{f}^{\circ}=\Delta{H}_{s}^{\circ}+\frac{1}{2}D+IE+\left(-EA\right)+\left(-{\Delta{H}}_{\text{lattice}}\right)\\ \text{Na}\left(s\right)+\frac{1}{2}{\text{Cl}}_{2}\left(g\right)\rightarrow\text{NaCl}\left(s\right)=-411\text{kJ}\end{array}[/latex]

Thus, the lattice energy can be calculated from other values. For cesium chloride, using this data, the lattice energy is:

[latex]\Delta{H}_{\text{lattice}}=\left(411+109+122+496+368\right)\text{kJ}=770\text{kJ}[/latex]

The Born-Haber cycle may also be used to calculate any one of the other quantities in the equation for lattice energy, provided that the remainder is known. For example, if the relevant enthalpy of sublimation [latex]\Delta{H}_{s}^{\circ},[/latex] ionization energy (IE), bond dissociation enthalpy (D), lattice energy ΔH_lattice, and standard enthalpy of formation [latex]\Delta{H}_{\text{f}}^{\circ}[/latex] are known, the Born-Haber cycle can be used to determine the electron affinity of an atom.

Lattice energies calculated for ionic compounds are typically much higher than bond dissociation energies measured for covalent bonds. Whereas lattice energies typically fall in the range of 600–4000 kJ/mol (some even higher), covalent bond dissociation energies are typically between 150–400 kJ/mol for single bonds. Keep in mind, however, that these are not directly comparable values. For ionic compounds, lattice energies are associated with many interactions, as cations and anions pack together in an extended lattice. For covalent bonds, the bond dissociation energy is associated with the interaction of just two atoms.

Key Takeaways

Lattice energies are often calculated using the Born-Haber cycle, a thermochemical cycle including all of the energetic steps involved in converting elements into an ionic compound.

Lattice energy for a solid MX: [latex]\text{MX}\left(s\right)\rightarrow{\text{M}}^{n\text{+}}\left(g\right)+{\text{X}}^{n-}\left(g\right)\Delta{H}_{\text{lattice}}[/latex]
Lattice energy for an ionic crystal: [latex]\Delta{H}_{\text{lattice}}=\frac{\text{k}\left({\text{Q}}^{\text{+}}\right)\left({\text{Q}}^{-}\right)}{{\text{d}}}[/latex]

Exercises

The lattice energy of LiF is 1023 kJ/mol, and the Li–F distance is 200.8 pm. NaF crystallizes in the same structure as LiF but with a Na–F distance of 231 pm. Which of the following values most closely approximates the lattice energy of NaF: 510, 890, 1023, 1175, or 4090 kJ/mol? Explain your choice.
For which of the following substances is the least energy required to convert one mole of the solid into separate ions?
1. MgO
2. SrO
3. KF
4. CsF
5. MgF₂
The reaction of a metal, M, with a halogen, X₂, proceeds by an exothermic reaction as indicated by this equation: [latex]\text{M}\left(s\right)+{\text{X}}_{2}\left(g\right)\rightarrow{\text{MX}}_{2}\left(s\right).[/latex] For each of the following, indicate which option will make the reaction more exothermic. Explain your answers.
1. a large radius vs. a small radius for M⁺²
2. a high ionization energy vs. a low ionization energy for M
3. an increasing bond energy for the halogen
4. a decreasing electron affinity for the halogen
5. an increasing size of the anion formed by the halogen
The lattice energy of LiF is 1023 kJ/mol, and the Li–F distance is 201 pm. MgO crystallizes in the same structure as LiF but with a Mg–O distance of 205 pm. Which of the following values most closely approximates the lattice energy of MgO: 256 kJ/mol, 512 kJ/mol, 1023 kJ/mol, 2046 kJ/mol, or 4090 kJ/mol? Explain your choice.
Which compound in each of the following pairs has the larger lattice energy? Note: Mg²⁺ and Li⁺ have similar radii; O^2– and F^– have similar radii. Explain your choices.
1. MgO or MgSe
2. LiF or MgO
3. Li₂O or LiCl
4. Li₂Se or MgO
Which compound in each of the following pairs has the larger lattice energy? Note: Ba²⁺ and K⁺ have similar radii; S^2– and Cl^– have similar radii. Explain your choices.
1. K₂O or Na₂O
2. K₂S or BaS
3. KCl or BaS
4. BaS or BaCl₂
Which of the following compounds requires the most energy to convert one mole of the solid into separate ions?
1. MgO
2. SrO
3. KF
4. CsF
5. MgF₂
Which of the following compounds requires the most energy to convert one mole of the solid into separate ions?
1. K₂S
2. K₂O
3. CaS
4. Cs₂S
5. CaO
The lattice energy of KF is 794 kJ/mol, and the interionic distance is 269 pm. The Na–F distance in NaF, which has the same structure as KF, is 231 pm. Which of the following values is the closest approximation of the lattice energy of NaF: 682 kJ/mol, 794 kJ/mol, 924 kJ/mol, 1588 kJ/mol, or 3175 kJ/mol? Explain your answer.

Selected Answers

1. The lattice energy is given by [latex]U=C\left(\frac{{Z}^{+}{Z}^{-}}{{R}_{o}}\right),[/latex] where R_o is the interatomic distance. The charges are the same in both LiF and NaF. The major difference is expected to be the interatomic distance 2.008 Å versus 2.31 Å. From the data for LiF, with Z⁺Z^– = –1, [latex]C=\frac{U{R}_{\text{o}}}{{Z}^{+}{Z}^{-}}=\frac{1023\times 2.008}{-1}=-2054\text{ kJ}\text{A}{\text{mol}}^{-1}[/latex].

Then, [latex]{U}_{\text{NaF}}=\frac{-2054\text{kJ}\text{A}{\text{mol}}^{-1}\left(-1\right)}{2.31\text{A}}=889\text{kJ}{\text{mol}}^{-1}\text{or }890{\text{ kJ mol}}^{-1}[/latex].

2. The lattice energy, U, is the energy required to convert the solid into separate ions. U may be calculated from the Born-Haber cycle.

The values in kJ/mol are approximately (a) 3791; (b) 3223; (c) 821; (d) 740; and (e) 2957.

The answer is (d), which requires about 740 kJ/mol.

3. In each case, think about how it would affect the Born-Haber cycle. Recall that the more negative the overall value, the more exothermic the reaction is.

The smaller the radius of the cation, the shorter the interionic distance and the greater the lattice energy would be. Since the lattice energy is negative in the Born-Haber cycle, this would lead to a more exothermic reaction.
A lower ionization energy is a lower positive energy in the Born-Haber cycle. This would make the reaction more exothermic, as a smaller positive value is “more exothermic.”
As in part (b), the bond energy is a positive energy. The lower it is, the more exothermic the reaction will be.
A higher electron affinity is more negative. In the Born-Haber cycle, the more negative the electron affinity, the more exothermic the overall reaction.
The smaller the radius of the anion, the shorter the interionic distance and the greater the lattice energy would be. Since the lattice energy is negative in the Born-Haber cycle, this would lead to a more exothermic reaction.

4. 4008 kJ/mol; both ions in MgO have twice the charge of the ions in LiF; the bond length is very similar and both have the same structure; a quadrupling of the energy is expected based on the equation for lattice energy

5. The compounds with the larger lattice energy are

MgO; selenium has larger radius than oxygen and, therefore, a larger interionic distance and thus, a larger smaller lattice energy than MgO
MgO; the higher charges on Mg and O, given the similar radii of the ions, leads to a larger lattice energy
Li₂O; the higher charge on O^2– leads to a larger energy; additionally, Cl^– is larger than O^2–; this leads to a larger interionic distance in LiCl and a lower lattice energy
MgO; the higher charge on Mg leads to a larger lattice energy

6. The compounds with the larger lattice energy are

Na₂O; Na⁺ has a smaller radius than K⁺
BaS; Ba has a larger charge than K
BaS; Ba and S have larger charges
BaS; S has a larger charge

7. MgO

8. CaO

9. 924 kJ/mol

Glossary

Born-Haber cycle: thermochemical cycle relating the various energetic steps involved in the formation of an ionic solid from the relevant elements

lattice energy (ΔH_lattice): energy required to separate one mole of an ionic solid into its component gaseous ions

Unit 11: Solutions and Colloids