Learning Outcomes
- Compute depreciation under accelerated methods
One of the most common accelerated methods of calculating depreciation is the double-declining-balance method (DDB). As the name implies, depreciation is calculated by doubling the straight-line rate and then applying that rate to the declining “value” of the asset.
For instance, in our last example, the straight-line rate for a 40-year asset would be 1/40 or 0.025, which is 2.5%. The double-declining-balance (DDB) rate would be 5%, but buildings are not often depreciated using accelerated methods, so let’s use a simple example: a small business owner comes to you and asks you to compare depreciating a $12,000 vehicle bought on Jan 1 with an estimated salvage value of $2,000 and a useful life of five years.
The straight-line computation would be $12,000 − $2,000 = depreciable value of $10,000. The depreciable value of $10,000 divided by 5 = $2,000 per year. The rate is ⅕, which is 0.20 or 20%. Since the asset was purchased at the beginning of January, there is no proration necessary. Depreciation under the straight-line method would look like this:
| 20X1 | 20X2 | 20X3 | 20X4 | 20X5 |
|---|---|---|---|---|
| $2,000 | $2,000 | $2,000 | $2,000 | $2,000 |
Under double-declining-balance (DDB), to compute periodic depreciation charges you begin by doubling the straight-line rate. In this case, the DDB rate would be 40% instead of 20%. Next, apply the DDB rate to the book value of the asset.
Book value is the original, historical cost minus accumulated depreciation (the depreciation taken so far). At the point where book value is equal to the salvage value, no more depreciation is taken.
For our client’s $12,000 vehicle, our calculation would look like this:
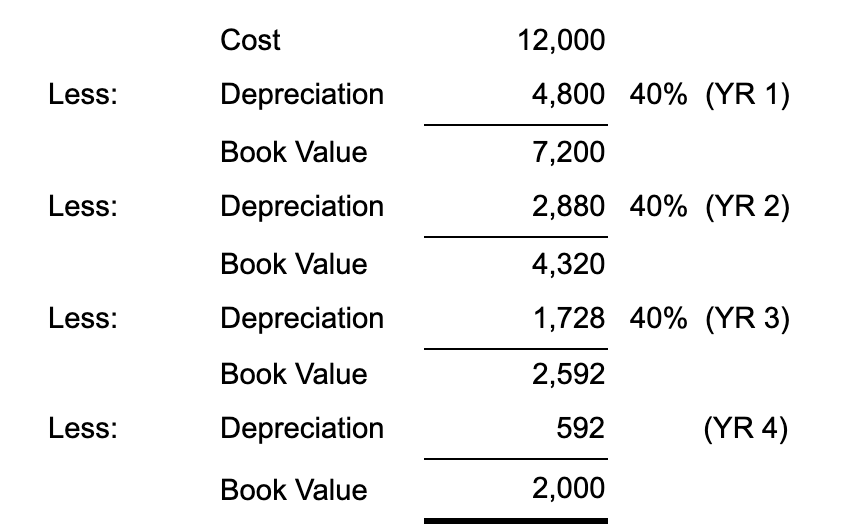
See the book value long description here.
Notice that we ignore the salvage value until the very end. Our year 4 (YR 4) depreciation expense would have been 40% of $2,592, except that would be $1036.80 which would have taken the ending book value down below $2,000. The ending book value, however, should always be equal to the salvage value (what we expect the asset to be worth when it is fully depreciated). So, in year 4, we only took $592 in depreciation, and then we are done.
In sum, we double the rate, and then apply that doubled rate to the DDB (book value).
Here are the two methods compared:
| 20X1 | 20X2 | 20X3 | 20X4 | 20X5 | |
|---|---|---|---|---|---|
| SL | $2,000 | $2,000 | $2,000 | $2,000 | $2,000 |
| DDB | $4,800 | $2,880 | $1,728 | $592 | $- |
And graphically:

Straight-line depreciation, graphically, is a straight-line. Accelerated depreciation records a larger amount of depreciation in the early years, thus accelerating the allocation of cost to the periods. This method may make more sense if you look at it theoretically graphed against the repair and maintenance costs of the vehicle, which would be very small in the first years and larger in later years:

In addition, notice that graphing the declining balance (book value) leads both methods to the same ending book value:

The DDB book value drops faster because of the accelerated cost being recognized on the income statement (depreciation expense).
Let’s run this calculation now for the delivery vehicle on our fixed asset list:
| As of 12/31/20X1 | |||
| Spivey Company | |||
| Asset | Description | Date Purchased | Cost |
|---|---|---|---|
| 1 | Land | 2/1/20X1 | 262,800 |
| 4 | Land | 10/1/20X1 | 120,000 |
| Total Land | 382,800 | ||
| 2 | Building | 7/1/20X1 | 490,000 |
| 5 | Building | 10/1/20X1 | 600,000 |
| Total Buildings | 1,090,000 | ||
| 3 | Machine | 7/1/20X1 | 162,000 |
| 6 | Delivery Van | 10/1/20X1 | 45,000 |
| 7 | Machine | 10/1/20X1 | 99,500 |
| 8 | Office Furniture | 10/1/20X1 | 70,000 |
| 9 | Computer | 10/1/20X1 | 5,500 |
| Total Machinery and Equipment | 382,000 | ||
| Total PP&E | $ 1,854,800 | ||
This is going to be more complicated because we bought the rig on October 1st, so we will have to prorate the first year’s depreciation:
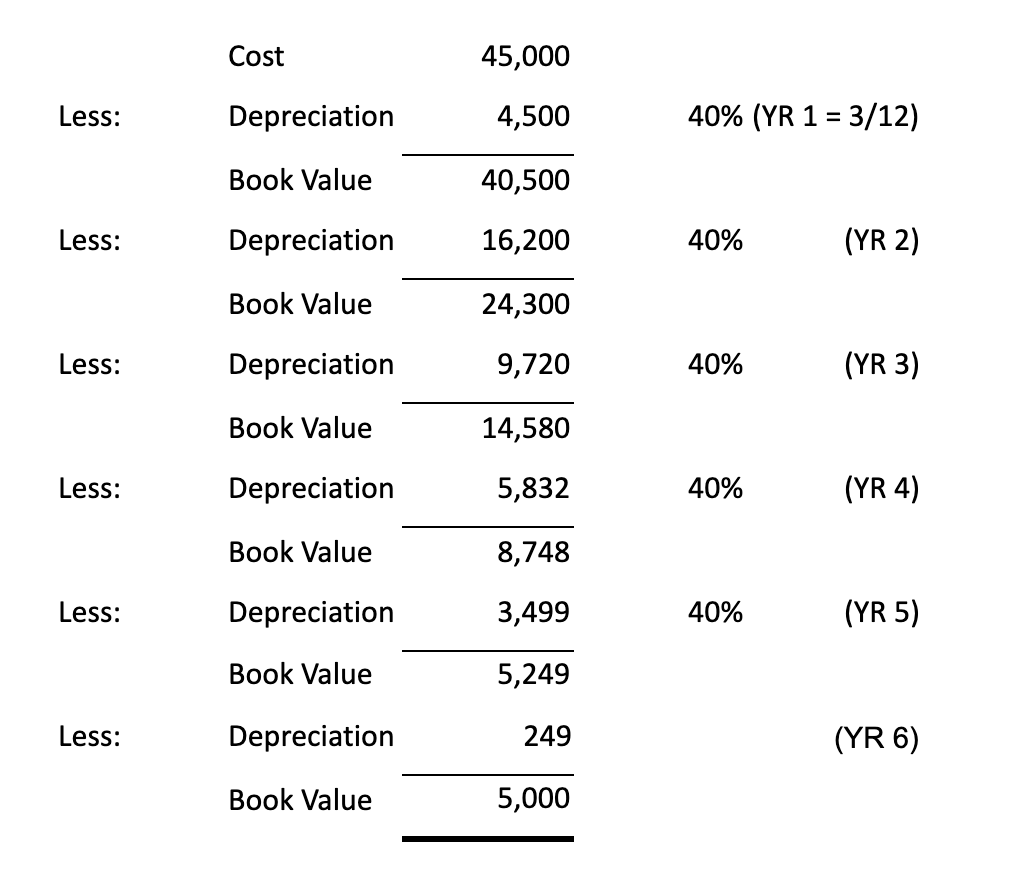
See the book value long description here.
There are six years because year one is a partial year, as is year six, which is simply the undepreciated amount left before the book value drops to salvage value.
PRACTICE QUESTION
Candela Citations
- Straight-Line Method. Authored by: Joseph Cooke. Provided by: Lumen Learning. License: CC BY: Attribution
