Basic Functions and Identities

Graphs of the Parent Functions

Three graphs side-by-side. From left to right, graph of the identify function, square function, and square root function. All three graphs extend from -4 to 4 on each axis.

Three graphs side-by-side. From left to right, graph of the cubic function, cube root function, and reciprocal function. All three graphs extend from -4 to 4 on each axis.

Three graphs side-by-side. From left to right, graph of the absolute value function, exponential function, and natural logarithm function. All three graphs extend from -4 to 4 on each axis.

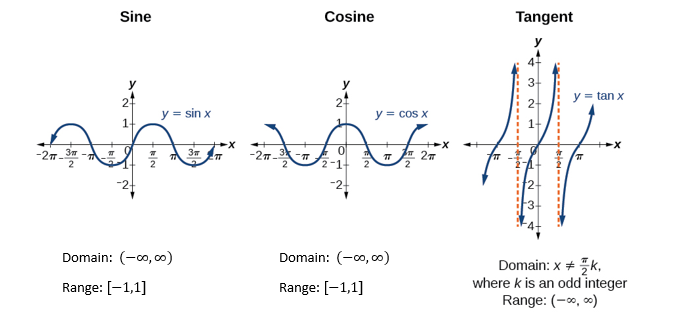
Graphs of the Trigonometric Functions

Three graphs of trigonometric functions side-by-side. From left to right, graph of the sine function, cosine function, and tangent function. Graphs of the sine and cosine functions extend from negative two pi to two pi on the x-axis and two to negative two on the y-axis. Graph of tangent extends from negative pi to pi on the x-axis and four to negative 4 on the y-axis.

Three graphs of trigonometric functions side-by-side. From left to right, graph of the cosecant function, secant function, and cotangent function. Graphs of the cosecant function and secant function extend from negative two pi to two pi on the x-axis and ten to negative ten on the y-axis. Graph of cotangent extends from negative two pi to two pi on the x-axis and twenty-five to negative twenty-five on the y-axis.

Three graphs of trigonometric functions side-by-side. From left to right, graph of the inverse sine function, inverse cosine function, and inverse tangent function. Graphs of the inverse sine and inverse tangent extend from negative pi over two to pi over two on the x-axis and pi over two to negative pi over two on the y-axis. Graph of inverse cosine extends from negative pi over two to pi on the x-axis and pi to negative pi over two on the y-axis.

Three graphs of trigonometric functions side-by-side. From left to right, graph of the inverse cosecant function, inverse secant function, and inverse cotangent function.

Trigonometric Identities

Pythagorean Identities	[latex]\begin{array}{l}{\mathrm{cos}}^{2}t+{\mathrm{sin}}^{2}t=1\\ 1+{\mathrm{tan}}^{2}t={\mathrm{sec}}^{2}t\\ 1+{\mathrm{cot}}^{2}t={\mathrm{csc}}^{2}t\end{array}[/latex]
Even-Odd Identities	[latex]\begin{array}{l}\mathrm{cos}\left(-t\right)=\mathrm{cos}\text{ }t\hfill \\ \mathrm{sec}\left(-t\right)=\mathrm{sec}\text{ }t\hfill \\ \mathrm{sin}\left(-t\right)=-\mathrm{sin}\text{ }t\hfill \\ \mathrm{tan}\left(-t\right)=-\mathrm{tan}\text{ }t\hfill \\ \mathrm{csc}\left(-t\right)=-\mathrm{csc}\text{ }t\hfill \\ \mathrm{cot}\left(-t\right)=-\mathrm{cot}\text{ }t\hfill \end{array}[/latex]
Cofunction Identities	[latex]\begin{array}{l}\mathrm{cos}\text{ }t=\mathrm{sin}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{sin}\text{ }t=\mathrm{cos}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{tan}\text{ }t=\mathrm{cot}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{cot}\text{ }t=\mathrm{tan}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{sec}\text{ }t=\mathrm{csc}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{csc}\text{ }t=\mathrm{sec}\left(\frac{\pi }{2}-t\right)\hfill \end{array}[/latex]
Fundamental Identities	[latex]\begin{array}{l}\mathrm{tan}\text{ }t=\frac{\mathrm{sin}\text{ }t}{\mathrm{cos}\text{ }t}\hfill \\ \mathrm{sec}\text{ }t=\frac{1}{\mathrm{cos}\text{ }t}\hfill \\ \mathrm{csc}\text{ }t=\frac{1}{\mathrm{sin}\text{ }t}\hfill \\ \text{cot}\text{ }t=\frac{1}{\text{tan}\text{ }t}=\frac{\text{cos}\text{ }t}{\text{sin}\text{ }t}\hfill \end{array}[/latex]
Sum and Difference Identities	[latex]\begin{array}{l}\mathrm{cos}\left(\alpha +\beta \right)=\mathrm{cos}\text{ }\alpha \text{ }\mathrm{cos}\text{ }\beta -\mathrm{sin}\text{ }\alpha \text{ }\mathrm{sin}\text{ }\beta \hfill \\ \mathrm{cos}\left(\alpha -\beta \right)=\mathrm{cos}\text{ }\alpha \text{ }\mathrm{cos}\text{ }\beta +\mathrm{sin}\text{ }\alpha \text{ }\mathrm{sin}\text{ }\beta \hfill \\ \mathrm{sin}\left(\alpha +\beta \right)=\mathrm{sin}\text{ }\alpha \text{ }\mathrm{cos}\text{ }\beta +\mathrm{cos}\text{ }\alpha \text{ }\mathrm{sin}\text{ }\beta \hfill \\ \mathrm{sin}\left(\alpha -\beta \right)=\mathrm{sin}\text{ }\alpha \text{ }\mathrm{cos}\text{ }\beta -\mathrm{cos}\text{ }\alpha \text{ }\mathrm{sin}\text{ }\beta \hfill \\ \mathrm{tan}\left(\alpha +\beta \right)=\frac{\mathrm{tan}\text{ }\alpha +\mathrm{tan}\text{ }\beta }{1-\mathrm{tan}\text{ }\alpha \text{ }\mathrm{tan}\text{ }\beta }\hfill \\ \mathrm{tan}\left(\alpha -\beta \right)=\frac{\mathrm{tan}\text{ }\alpha -\mathrm{tan}\text{ }\beta }{1+\mathrm{tan}\text{ }\alpha \text{ }\mathrm{tan}\text{ }\beta }\hfill \end{array}[/latex]
Double-Angle Formulas	[latex]\begin{array}{l}\mathrm{sin}\left(2\theta \right)=2\text{ }\mathrm{sin}\text{ }\theta \text{ }\mathrm{cos}\text{ }\theta \hfill \\ \mathrm{cos}\left(2\theta \right)={\mathrm{cos}}^{2}\theta -{\mathrm{sin}}^{2}\theta \hfill \\ \mathrm{cos}\left(2\theta \right)=1-2\text{ }{\mathrm{sin}}^{2}\theta \hfill \\ \mathrm{cos}\left(2\theta \right)=2\text{ }{\mathrm{cos}}^{2}\theta -1\hfill \\ \mathrm{tan}\left(2\theta \right)=\frac{2\text{ }\mathrm{tan}\text{ }\theta }{1-{\mathrm{tan}}^{2}\theta }\hfill \end{array}[/latex]
Half-Angle Formulas	[latex]\begin{array}{l}\mathrm{sin}\text{ }\frac{\alpha }{2}=±\sqrt{\frac{1-\mathrm{cos}\text{ }\alpha }{2}}\hfill \\ \mathrm{cos}\text{ }\frac{\alpha }{2}=±\sqrt{\frac{1+\mathrm{cos}\text{ }\alpha }{2}}\hfill \\ \mathrm{tan}\text{ }\frac{\alpha }{2}=±\sqrt{\frac{1-\mathrm{cos}\text{ }\alpha }{1+\mathrm{cos}\text{ }\alpha }}\hfill \\ \mathrm{tan}\text{ }\frac{\alpha }{2}=\frac{\mathrm{sin}\text{ }\alpha }{1+\mathrm{cos}\text{ }\alpha }\hfill \\ \mathrm{tan}\text{ }\frac{\alpha }{2}=\frac{1-\mathrm{cos}\text{ }\alpha }{\mathrm{sin}\text{ }\alpha }\hfill \end{array}[/latex]
Reduction Formulas	[latex]\begin{array}{l}{\mathrm{sin}}^{2}\theta =\frac{1-\mathrm{cos}\left(2\theta \right)}{2}\\ {\mathrm{cos}}^{2}\theta =\frac{1+\mathrm{cos}\left(2\theta \right)}{2}\\ {\mathrm{tan}}^{2}\theta =\frac{1-\mathrm{cos}\left(2\theta \right)}{1+\mathrm{cos}\left(2\theta \right)}\end{array}[/latex]
Product-to-Sum Formulas	[latex]\begin{array}{l}\mathrm{cos}\text{ }\alpha \text{ }\mathrm{cos}\text{ }\beta =\frac{1}{2}\left[\mathrm{cos}\left(\alpha -\beta \right)+\mathrm{cos}\left(\alpha +\beta \right)\right]\hfill \\ \mathrm{sin}\text{ }\alpha \text{ }\mathrm{cos}\text{ }\beta =\frac{1}{2}\left[\mathrm{sin}\left(\alpha +\beta \right)+\mathrm{sin}\left(\alpha -\beta \right)\right]\hfill \\ \mathrm{sin}\text{ }\alpha \text{ }\mathrm{sin}\text{ }\beta =\frac{1}{2}\left[\mathrm{cos}\left(\alpha -\beta \right)-\mathrm{cos}\left(\alpha +\beta \right)\right]\hfill \\ \mathrm{cos}\text{ }\alpha \text{ }\mathrm{sin}\text{ }\beta =\frac{1}{2}\left[\mathrm{sin}\left(\alpha +\beta \right)-\mathrm{sin}\left(\alpha -\beta \right)\right]\hfill \end{array}[/latex]
Sum-to-Product Formulas	[latex]\begin{array}{l}\mathrm{sin}\text{ }\alpha +\mathrm{sin}\text{ }\beta =2\text{ }\mathrm{sin}\left(\frac{\alpha +\beta }{2}\right)\text{ }\mathrm{cos}\left(\frac{\alpha -\beta }{2}\right)\hfill \\ \mathrm{sin}\text{ }\alpha -\mathrm{sin}\text{ }\beta =2\text{ }\mathrm{sin}\left(\frac{\alpha -\beta }{2}\right)\text{ }\mathrm{cos}\left(\frac{\alpha +\beta }{2}\right)\hfill \\ \mathrm{cos}\text{ }\alpha -\mathrm{cos}\text{ }\beta =-2\text{ }\mathrm{sin}\left(\frac{\alpha +\beta }{2}\right)\text{ }\mathrm{sin}\left(\frac{\alpha -\beta }{2}\right)\hfill \\ \mathrm{cos}\text{ }\alpha +\mathrm{cos}\text{ }\beta =2\text{ }\mathrm{cos}\left(\frac{\alpha +\beta }{2}\right)\text{ }\mathrm{cos}\left(\frac{\alpha -\beta }{2}\right)\hfill \end{array}[/latex]
Law of Sines	[latex]\begin{array}{l}\frac{\mathrm{sin}\text{ }\alpha }{a}=\frac{\mathrm{sin}\text{ }\beta }{b}=\frac{\mathrm{sin}\text{ }\gamma }{c}\hfill \\ \frac{a}{\mathrm{sin}\text{ }\alpha }=\frac{b}{\mathrm{sin}\text{ }\beta }=\frac{c}{\mathrm{sin}\text{ }\gamma }\hfill \end{array}[/latex]
Law of Cosines	[latex]\begin{array}{l}{a}^{2}={b}^{2}+{c}^{2}-2bc\text{ }\mathrm{cos}\text{ }\alpha \hfill \\ {b}^{2}={a}^{2}+{c}^{2}-2ac\text{ }\mathrm{cos}\text{ }\beta \hfill \\ {c}^{2}={a}^{2}+{b}^{2}-2ab\text{ }\text{cos}\text{ }\gamma \hfill \end{array}[/latex]