1.2 Section Exercises

1.2 Section Exercises

Verbal

1. Why does the domain differ for different functions?

2. How do we determine the domain of a function defined by an equation?

3. Explain why the domain of[latex]\text{ }f\left(x\right)=\sqrt[3]{x}\text{ }[/latex]is different from the domain of[latex]\text{ }f\left(x\right)=\sqrt[]{x}.[/latex]

4. When describing sets of numbers using interval notation, when do you use a parenthesis and when do you use a bracket?

5. How do you graph a piecewise function?

Algebraic

For the following exercises, find the domain of each function using interval notation.

6. [latex]f\left(x\right)=-2x\left(x-1\right)\left(x-2\right)[/latex]

7. [latex]f\left(x\right)=5-2{x}^{2}[/latex]

8. [latex]f\left(x\right)=3\sqrt{x-2}[/latex]

9. [latex]f\left(x\right)=3-\sqrt{6-2x}[/latex]

10. [latex]f\left(x\right)=\sqrt{4-3x}[/latex]

11. [latex]\begin{array}{l}\\ f\left(x\right)=\sqrt[]{{x}^{2}+4}\end{array}[/latex]

12. [latex]f\left(x\right)=\sqrt[3]{1-2x}[/latex]

13. [latex]f\left(x\right)=\sqrt[3]{x-1}[/latex]

14. [latex]f\left(x\right)=\frac{9}{x-6}[/latex]

15. [latex]f\left(x\right)=\frac{3x+1}{4x+2}[/latex]

16. [latex]f\left(x\right)=\frac{\sqrt{x+4}}{x-4}[/latex]

17. [latex]f\left(x\right)=\frac{x-3}{{x}^{2}+9x-22}[/latex]

18. [latex]f\left(x\right)=\frac{1}{{x}^{2}-x-6}[/latex]

19. [latex]f\left(x\right)=\frac{2{x}^{3}-250}{{x}^{2}-2x-15}[/latex]

20. [latex]\frac{5}{\sqrt{x-3}}[/latex]

21. [latex]\frac{2x+1}{\sqrt{5-x}}[/latex]

22. [latex]f\left(x\right)=\frac{\sqrt{x-4}}{\sqrt{x-6}}[/latex]

23. [latex]f\left(x\right)=\frac{\sqrt{x-6}}{\sqrt{x-4}}[/latex]

24. [latex]f\left(x\right)=\frac{x}{x}[/latex]

25. [latex]f\left(x\right)=\frac{{x}^{2}-9x}{{x}^{2}-81}[/latex]

26. Find the domain of the function[latex]\text{ }f\left(x\right)=\sqrt{2{x}^{3}-50x}\text{ }[/latex]by:

  1. using algebra.
  2. graphing the function in the radicand and determining intervals on the x-axis for which the radicand is nonnegative.

Graphical

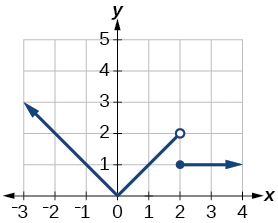
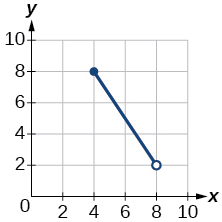
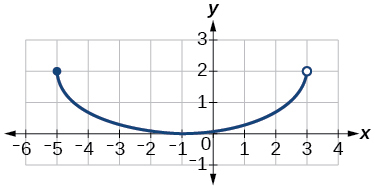
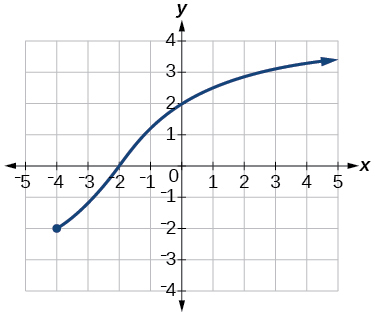
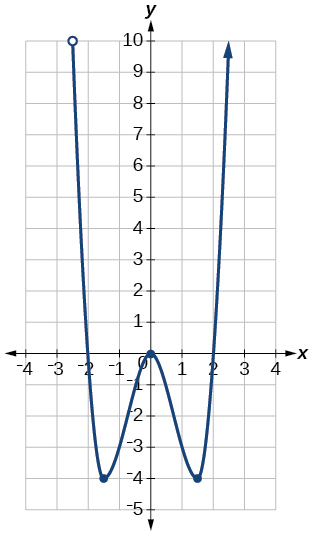
For the following exercises, write the domain and range of each function using interval notation.

27.
 Graph of a function from (2, 8].

28. 
Graph of a function from [4, 8).
29. 
Graph of a function from [-4, 4].

30. 
Graph of a function from [2, 6].
31. 
Graph of a function from [-5, 3).

32. 
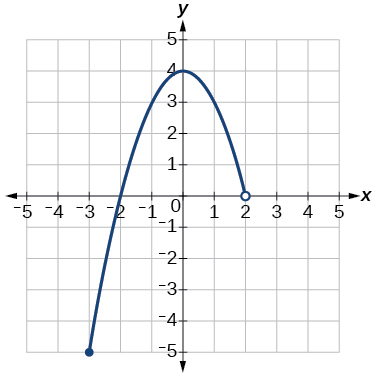
Graph of a function from [-3, 2).
33. 
Graph of a function from (-infinity, 2].

34. 
Graph of a function from [-4, infinity).
35.
Graph of a function from [-6, -1/6]U[1/6, 6]/.

36. 
Graph of a function from (-2.5, infinity).
37. 
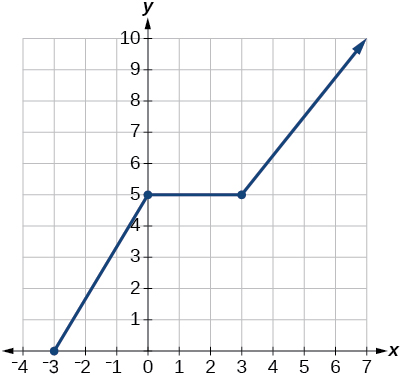
Graph of a function from [-3, infinity).

For the following exercises, sketch a graph of the piecewise function. Write the domain in interval notation.

38. [latex]f\left(x\right)=\bigg\{\begin{array}{lll}x+1\hfill & \text{if}\hfill & x<-2\hfill \\ -2x-3\hfill & \text{if}\hfill & x\ge -2\hfill \end{array}[/latex]

39. [latex]f\left(x\right)=\bigg\{\begin{array}{lll}2x-1\hfill & \text{if}\hfill & x<1\hfill \\ 1+x\hfill & \text{if}\hfill & x\ge 1\hfill \end{array}[/latex]

40. [latex]f\left(x\right)=\bigg\{\begin{array}{c}x+1\text{ }\text{ }\text{if}\text{ }\text{ }x<0\\ x-1\text{ }\text{ }\text{if}\text{ }\text{ }\text{ }x>0\end{array}[/latex]

41. [latex]f\left(x\right)=\bigg\{\begin{array}{ccc}3& \text{if}& x<0\\ \sqrt{x}& \text{if}& x\ge 0\end{array}[/latex]

42. [latex]f\left(x\right)=\bigg\{\begin{array}{c}{x}^{2}\text{ if }x<0\\ 1-x\text{ if }x>0\end{array}[/latex]

43. [latex]f\left(x\right)=\bigg\{\begin{array}{r}\hfill \begin{array}{r}\hfill {x}^{2}\\ \hfill x+2\end{array}\end{array}\text{ }\text{ }\begin{array}{l}\text{if}\text{ }\text{ }\text{ }\text{ }\text{ }x<0\hfill \\ \text{if}\text{ }\text{ }\text{ }\text{ }\text{ }x\ge 0\hfill \end{array}[/latex]

44. [latex]f\left(x\right)=\bigg\{\begin{array}{ccc}x+1& \text{if}& x<1\\ {x}^{3}& \text{if}& x\ge 1\end{array}[/latex]

45. [latex]f\left(x\right)=\bigg\{\begin{array}{c}|x|\\ 1\end{array}\begin{array}{l}\text{ }\text{ }\text{ }\text{if}\text{ }\text{ }\text{ }x<2\hfill \\ \text{ }\text{ }\text{ }\text{if}\text{ }\text{ }\text{ }x\ge 2\hfill \end{array}[/latex]

Numeric

For the following exercises, given each function [latex]f,[/latex]evaluate [latex]f\left(-3\right),\text{ }f\left(-2\right),\text{ }f\left(-1\right),[/latex] and [latex]f\left(0\right).[/latex]

46. [latex]f\left(x\right)=\bigg\{\begin{array}{lll}x+1\hfill & \text{if}\hfill & x<-2\hfill \\ -2x-3\hfill & \text{if}\hfill & x\ge -2\hfill \end{array}[/latex]

47. [latex]f\left(x\right)=\bigg\{\begin{array}{cc}1& \text{if }x\le -3\\ 0& \text{if }x>-3\end{array}[/latex]

48. [latex]f\left(x\right)=\bigg\{\begin{array}{cc}-2{x}^{2}+3& \text{if }x\le -1\\ 5x-7& \text{if }x>-1\end{array}[/latex]

For the following exercises, given each function[latex]\text{ }f,\text{ }[/latex]evaluate[latex]f\left(-1\right),\text{ }f\left(0\right),\text{ }f\left(2\right),\text{ }[/latex]and[latex]\text{ }f\left(4\right).[/latex]

49. [latex]f\left(x\right)=\bigg\{\begin{array}{lll}7x+3\hfill & \text{if}\hfill & x<0\hfill \\ 7x+6\hfill & \text{if}\hfill & x\ge 0\hfill \end{array}[/latex]

50. [latex]f\left(x\right)=\bigg\{\begin{array}{ccc}{x}^{2}-2& \text{if}& x<2\\ 4+|x-5|& \text{if}& x\ge 2\end{array}[/latex]

51. [latex]f\left(x\right)=\Bigg\{\begin{array}{ccc}5x& \text{if}& x<0\\ 3& \text{if}& 0\le x\le 3\\ {x}^{2}& \text{if}& x>3\end{array}[/latex]

For the following exercises, write the domain for the piecewise function in interval notation.

52. [latex]f\left(x\right)=\bigg\{\begin{array}{c}x+1\text{ }\text{ }\text{ }\text{ }\text{ }\text{ if}\text{ }\text{ }x<-2\\ -2x-3\text{ }\text{ }\text{if}\text{ }\text{ }x\ge -2\end{array}[/latex]

53. [latex]f\left(x\right)=\bigg\{\begin{array}{c}{x}^{2}-2\text{ }\text{ }\text{ }\text{ }\text{ }\text{ if}\text{ }\text{ }x<1\\ -{x}^{2}+2\text{ }\text{ }\text{if}\text{ }\text{ }x>1\end{array}[/latex]

54. [latex]f\left(x\right)=\bigg\{\begin{array}{c}2x-3\\ -3{x}^{2}\end{array}\text{ }\text{ }\begin{array}{c}\text{if}\text{ }\text{ }\text{ }x<0\\ \text{if}\text{ }\text{ }\text{ }x\ge 2\end{array}[/latex]

Technology

55. Graph[latex]\text{ }y=\frac{1}{{x}^{2}}\text{ }[/latex]on the viewing window[latex]\text{ }\left[-0.5,-0.1\right]\text{ }[/latex]and[latex]\text{ }\left[0.1,0.5\right].\text{ }[/latex]Determine the corresponding range for the viewing window. Show the graphs.

Graph of the equation from [-0.5, -0.1].

window:[latex]\text{ }\left[-0.5,-0.1\right];\text{ }[/latex]range:[latex]\text{ }\left[4,\text{ }100\right][/latex]

Graph of the equation from [0.1, 0.5].

 

window:[latex]\text{ }\left[0.1,\text{ }0.5\right];\text{ }[/latex]range:[latex]\text{ }\left[4,\text{ }100\right][/latex]

56. Graph[latex]\text{ }y=\frac{1}{x}\text{ }[/latex]on the viewing window[latex]\text{ }\left[-0.5,-0.1\right]\text{ }[/latex]and[latex]\text{ }\left[0.1,\text{ }0.5\right].\text{ }[/latex]Determine the corresponding range for the viewing window. Show the graphs.

Extension

57. Suppose the range of a function[latex]\text{ }f\text{ }[/latex]is[latex]\text{ }\left[-5,\text{ }8\right].\text{ }[/latex]What is the range of[latex]\text{ }|f\left(x\right)|?[/latex]

58. Create a function in which the range is all nonnegative real numbers.

59. Create a function in which the domain is[latex]\text{ }x>2.[/latex]

Real-World Applications

60. The height[latex]\text{ }h\text{ }[/latex]of a projectile is a function of the time[latex]\text{ }t\text{ }[/latex]it is in the air. The height in feet for[latex]\text{ }t\text{ }[/latex]seconds is given by the function [latex]h\left(t\right)=-16{t}^{2}+96t.[/latex] What is the domain of the function? What does the domain mean in the context of the problem?

61. The cost in dollars of making[latex]\text{ }x\text{ }[/latex]items is given by the function[latex]\text{ }C\left(x\right)=10x+500.[/latex]

  1. The fixed cost is determined when zero items are produced. Find the fixed cost for this item.
  2. What is the cost of making 25 items?
  3. Suppose the maximum cost allowed is $1500. What are the domain and range of the cost function,[latex]\text{ }C\left(x\right)?[/latex]