2.1 Section Exercises
Verbal
1. Describe why the horizontal line test is an effective way to determine whether a function is one-to-one?
2. Why do we restrict the domain of the function[latex]\text{ }f\left(x\right)={x}^{2}\text{ }[/latex]to find the function’s inverse?
3. Can a function be its own inverse? Explain.
4. Are one-to-one functions either always increasing or always decreasing? Why or why not?
5. How do you find the inverse of a function algebraically?
Algebraic
6. Show that the function[latex]\text{ }f\left(x\right)=a-x\text{ }[/latex]is its own inverse for all real numbers[latex]\text{ }a.\text{ }[/latex]
For the following exercises, find[latex]\text{ }{f}^{-1}\left(x\right)\text{ }[/latex]for each function.
7. [latex]f\left(x\right)=x+3[/latex]
8. [latex]f\left(x\right)=x+5[/latex]
9. [latex]f\left(x\right)=2-x[/latex]
10. [latex]f\left(x\right)=3-x[/latex]
11. [latex]f\left(x\right)=\frac{x}{x+2}[/latex]
12. [latex]f\left(x\right)=\frac{2x+3}{5x+4}[/latex]
For the following exercises, find a domain on which each function[latex]\text{ }f\text{ }[/latex]is one-to-one and non-decreasing. Write the domain in interval notation. Then find the inverse of[latex]\text{ }f\text{ }[/latex]restricted to that domain.
13. [latex]f\left(x\right)={\left(x+7\right)}^{2}[/latex]
14. [latex]f\left(x\right)={\left(x-6\right)}^{2}[/latex]
15. [latex]f\left(x\right)={x}^{2}-5[/latex]
16. Given[latex]\text{ }f\left(x\right)=\frac{x}{2+x}\text{ }[/latex]and[latex]\text{ }g\left(x\right)=\frac{2x}{1-x}:[/latex]
- Find[latex]\text{ }f\left(g\left(x\right)\right)\text{ }[/latex]and[latex]\text{ }g\left(f\left(x\right)\right).[/latex]
- What does the answer tell us about the relationship between[latex]\text{ }f\left(x\right)\text{ }[/latex]and[latex]\text{ }g\left(x\right)?[/latex]
For the following exercises, use function composition to verify that[latex]\text{ }f\left(x\right)\text{ }[/latex]and[latex]\text{ }g\left(x\right)\text{ }[/latex]are inverse functions.
17. [latex]f\left(x\right)=\sqrt[3]{x-1}\text{ }[/latex]and[latex]\text{ }g\left(x\right)={x}^{3}+1[/latex]
18. [latex]f\left(x\right)=-3x+5\text{ }[/latex]and[latex]\text{ }g\left(x\right)=\frac{x-5}{-3}[/latex]
Graphical
For the following exercises, use a graphing utility to determine whether each function is one-to-one.
19. [latex]f\left(x\right)=\sqrt{x}[/latex]
20. [latex]f\left(x\right)=\sqrt[3]{3x+1}[/latex]
21. [latex]f\left(x\right)=-5x+1[/latex]
22. [latex]f\left(x\right)={x}^{3}-27[/latex]
For the following exercises, determine whether the graph represents a one-to-one function.
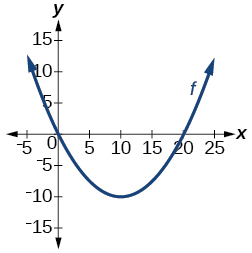
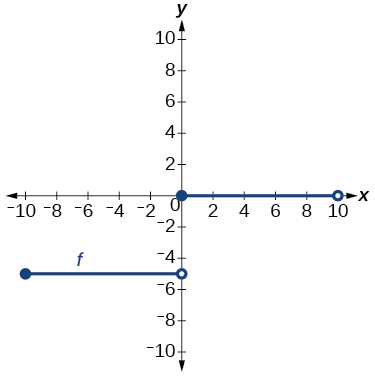
For the following exercises, use the graph of[latex]\text{ }f\text{ }[/latex]shown in (Figure).
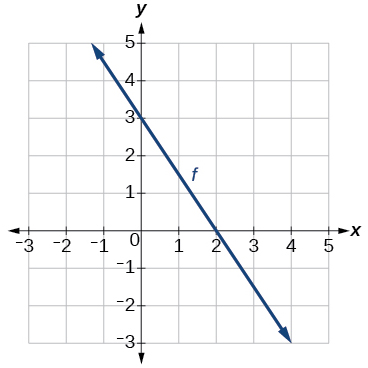
Figure 11.
25.Find[latex]\text{ }f\left(0\right).[/latex]
26. Solve[latex]\text{ }f\left(x\right)=0.[/latex]
27. Find[latex]\text{ }{f}^{-1}\left(0\right).[/latex]
28. Solve[latex]\text{ }{f}^{-1}\left(x\right)=0.[/latex]
For the following exercises, use the graph of the one-to-one function shown in (Figure).
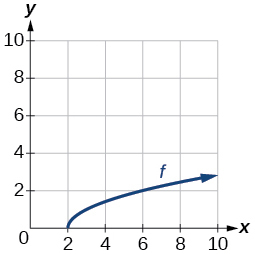
Figure 12.
29. Sketch the graph of[latex]\text{ }{f}^{-1}.\text{ }[/latex]
30. Find[latex]\text{ }f\left(6\right)\text{ and }{f}^{-1}\left(2\right).[/latex]
31. If the complete graph of[latex]\text{ }f\text{ }[/latex]is shown, find the domain of[latex]\text{ }f.\text{ }[/latex]
32. If the complete graph of[latex]\text{ }f\text{ }[/latex]is shown, find the range of[latex]\text{ }f.[/latex]
Numeric
For the following exercises, evaluate or solve, assuming that the function[latex]\text{ }f\text{ }[/latex]is one-to-one.
33. If[latex]\text{ }f\left(6\right)=7,\text{ }[/latex]find[latex]\text{ }\text{ }{f}^{-1}\left(7\right).[/latex]
34. If[latex]\text{ }f\left(3\right)=2,\text{ }[/latex]find[latex]\text{ }{f}^{-1}\left(2\right).[/latex]
35. If[latex]\text{ }{f}^{-1}\left(-4\right)=-8,\text{ }[/latex]find[latex]\text{ }f\left(-8\right).[/latex]
36. If[latex]\text{ }{f}^{-1}\left(-2\right)=-1,\text{ }[/latex]find[latex]\text{ }f\left(-1\right).[/latex]
For the following exercises, use the values listed in (Figure) to evaluate or solve.
| Table 6 |
|
| [latex]x[/latex] | [latex]f\left(x\right)[/latex] |
| 0 | 8 |
| 1 | 0 |
| 2 | 7 |
| 3 | 4 |
| 4 | 2 |
| 5 | 6 |
| 6 | 5 |
| 7 | 3 |
| 8 | 9 |
| 9 | 1 |
37. Find[latex]\text{ }f\left(1\right).[/latex]
38. Solve[latex]\text{ }f\left(x\right)=3.[/latex]
39. Find[latex]\text{ }{f}^{-1}\left(0\right).[/latex]
40. Solve[latex]\text{ }{f}^{-1}\left(x\right)=7.[/latex]
41. Use the tabular representation of[latex]\text{ }f\text{ }[/latex]in (Figure) to create a table for[latex]\text{ }{f}^{-1}\left(x\right).[/latex]
| Table 7 | |||||
| [latex]x[/latex] | 3 | 6 | 9 | 13 | 14 |
| [latex]f\left(x\right)[/latex] | 1 | 4 | 7 | 12 | 16 |
Technology
For the following exercises, find the inverse function. Then, graph the function and its inverse.
42. [latex]f\left(x\right)=\frac{3}{x-2}[/latex]
43. [latex]f\left(x\right)={x}^{3}-1[/latex]
44. Find the inverse function of[latex]\text{ }f\left(x\right)=\frac{1}{x-1}.\text{ }[/latex]Use a graphing utility to find its domain and range. Write the domain and range in interval notation.
Real-World Applications
45. To convert from[latex]\text{ }x\text{ }[/latex]degrees Celsius to[latex]\text{ }y\text{ }[/latex]degrees Fahrenheit, we use the formula[latex]\text{ }f\left(x\right)=\frac{9}{5}x+32.\text{ }[/latex]Find the inverse function, if it exists, and explain its meaning.
46. The circumference[latex]\text{ }C\text{ }[/latex]of a circle is a function of its radius given by[latex]\text{ }C\left(r\right)=2\pi r.\text{ }[/latex]Express the radius of a circle as a function of its circumference. Call this function[latex]\text{ }r\left(C\right).\text{ }[/latex]Find[latex]\text{ }r\left(36\pi \right)\text{ }[/latex]and interpret its meaning.
47. A car travels at a constant speed of 50 miles per hour. The distance the car travels in miles is a function of time,[latex]\text{ }t,\text{ }[/latex]in hours given by[latex]\text{ }d\left(t\right)=50t.\text{ }[/latex]Find the inverse function by expressing the time of travel in terms of the distance traveled. Call this function[latex]\text{ }t\left(d\right).\text{ }[/latex]Find[latex]\text{ }t\left(180\right)\text{ }[/latex]and interpret its meaning.


