2.6 Section Exercises

2.6 Section Exercises

Verbal

1. The inverse of every logarithmic function is an exponential function and vice-versa. What does this tell us about the relationship between the coordinates of the points on the graphs of each?

2. What type(s) of translation(s), if any, affect the range of a logarithmic function?

3. What type(s) of translation(s), if any, affect the domain of a logarithmic function?

4. Shifting the function right or left and reflecting the function about the y-axis will affect its domain.

5. Consider the general logarithmic function[latex]\text{ }f\left(x\right)={\mathrm{log}}_{b}\left(x\right).\text{ }[/latex]Why can’t[latex]\text{ }x\text{ }[/latex]be zero?

6. Does the graph of a general logarithmic function have a horizontal asymptote? Explain.

Algebraic

For the following exercises, state the domain and range of the function.

7. [latex]f\left(x\right)={\mathrm{log}}_{3}\left(x+4\right)[/latex]

8. [latex]h\left(x\right)=\mathrm{ln}\left(\frac{1}{2}-x\right)[/latex]

9. [latex]g\left(x\right)={\mathrm{log}}_{5}\left(2x+9\right)-2[/latex]

10. [latex]h\left(x\right)=\mathrm{ln}\left(4x+17\right)-5[/latex]

11. [latex]f\left(x\right)={\mathrm{log}}_{2}\left(12-3x\right)-3[/latex]

For the following exercises, state the domain and the vertical asymptote of the function.

12. [latex]\text{ }f\left(x\right)={\mathrm{log}}_{b}\left(x-5\right)[/latex]

13. [latex]\text{ }g\left(x\right)=\mathrm{ln}\left(3-x\right)[/latex]

14. [latex]\text{ }f\left(x\right)=\mathrm{log}\left(3x+1\right)[/latex]

15. [latex]\text{ }f\left(x\right)=3\mathrm{log}\left(-x\right)+2[/latex]

16. [latex]\text{ }g\left(x\right)=-\mathrm{ln}\left(3x+9\right)-7[/latex]

For the following exercises, state the domain, vertical asymptote, and end behavior of the function.

17. [latex]f\left(x\right)=\mathrm{ln}\left(2-x\right)[/latex]

18. [latex]f\left(x\right)=\mathrm{log}\left(x-\frac{3}{7}\right)[/latex]

19. Vertical asymptote: [latex]x=\frac{3}{7}[/latex]; End behavior: as [latex]x\to {\left(\frac{3}{7}\right)}^{+},f\left(x\right)\to -\infty[/latex] and as [latex]x\to \infty ,f\left(x\right)\to \infty[/latex]

20. [latex]h\left(x\right)=-\mathrm{log}\left(3x-4\right)+3[/latex]

21. [latex]g\left(x\right)=\mathrm{ln}\left(2x+6\right)-5[/latex]

22. End behavior: as [latex]x\to -{3}^{+}[/latex], [latex]f\left(x\right)\to -\infty[/latex] and as [latex]x\to \infty[/latex], [latex]f\left(x\right)\to \infty[/latex]

23. [latex]f\left(x\right)={\mathrm{log}}_{3}\left(15-5x\right)+6[/latex]

For the following exercises, state the domain, range, and x– and y-intercepts, if they exist. If they do not exist, write DNE.

24. [latex]h\left(x\right)={\mathrm{log}}_{4}\left(x-1\right)+1[/latex]

25. [latex]f\left(x\right)=\mathrm{log}\left(5x+10\right)+3[/latex]

26. [latex]g\left(x\right)=\mathrm{ln}\left(-x\right)-2[/latex]

27. [latex]f\left(x\right)={\mathrm{log}}_{2}\left(x+2\right)-5[/latex]

28. [latex]h\left(x\right)=3\mathrm{ln}\left(x\right)-9[/latex]

Graphical

For the following exercises, match each function in (Figure) with the letter corresponding to its graph.

Graph of five logarithmic functions.

Figure 17.

29. [latex]d\left(x\right)=\mathrm{log}\left(x\right)[/latex]

30. [latex]f\left(x\right)=\mathrm{ln}\left(x\right)[/latex]

31. [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex]

32. [latex]h\left(x\right)={\mathrm{log}}_{5}\left(x\right)[/latex]

33. [latex]j\left(x\right)={\mathrm{log}}_{25}\left(x\right)[/latex]

For the following exercises, match each function in (Figure) with the letter corresponding to its graph.

Graph of three logarithmic functions.

Figure 18.

34. [latex]f\left(x\right)={\mathrm{log}}_{\frac{1}{3}}\left(x\right)[/latex]

35. [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex]

36. [latex]h\left(x\right)={\mathrm{log}}_{\frac{3}{4}}\left(x\right)[/latex]

For the following exercises, sketch the graphs of each pair of functions on the same axis.

37. [latex]f\left(x\right)=\mathrm{log}\left(x\right)\text{ }[/latex]and[latex]\text{ }g\left(x\right)={10}^{x}[/latex]

38. [latex]f\left(x\right)=\mathrm{log}\left(x\right)\text{ }[/latex]and[latex]\text{ }g\left(x\right)={\mathrm{log}}_{\frac{1}{2}}\left(x\right)[/latex]

39. [latex]f\left(x\right)={\mathrm{log}}_{4}\left(x\right)\text{ }[/latex]and[latex]\text{ }g\left(x\right)=\mathrm{ln}\left(x\right)[/latex]

40. [latex]f\left(x\right)={e}^{x}\text{ }[/latex]and[latex]\text{ }g\left(x\right)=\mathrm{ln}\left(x\right)[/latex]

For the following exercises, match each function in (Figure) with the letter corresponding to its graph.

Graph of three logarithmic functions.

Figure 19.

41. [latex]f\left(x\right)={\mathrm{log}}_{4}\left(-x+2\right)[/latex]

42. [latex]g\left(x\right)=-{\mathrm{log}}_{4}\left(x+2\right)[/latex]

43. [latex]h\left(x\right)={\mathrm{log}}_{4}\left(x+2\right)[/latex]

For the following exercises, sketch the graph of the indicated function.

44. [latex]\text{ }f\left(x\right)={\mathrm{log}}_{2}\left(x+2\right)[/latex]

45. [latex]\text{ }f\left(x\right)=2\mathrm{log}\left(x\right)[/latex]

46. [latex]\text{ }f\left(x\right)=\mathrm{ln}\left(-x\right)[/latex]

47. [latex]g\left(x\right)=\mathrm{log}\left(4x+16\right)+4[/latex]

48. [latex]g\left(x\right)=\mathrm{log}\left(6-3x\right)+1[/latex]

49. [latex]h\left(x\right)=-\frac{1}{2}\mathrm{ln}\left(x+1\right)-3[/latex]

For the following exercises, write a logarithmic equation corresponding to the graph shown.

50. Use[latex]\text{ }y={\mathrm{log}}_{2}\left(x\right)\text{ }[/latex]as the parent function.

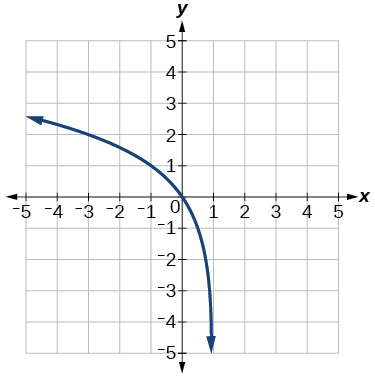
The graph y=log_2(x) has been reflected over the y-axis and shifted to the right by 1.

51. Use[latex]\text{ }f\left(x\right)={\mathrm{log}}_{3}\left(x\right)\text{ }[/latex]as the parent function.

The graph y=log_3(x) has been reflected over the x-axis, vertically stretched by 3, and shifted to the left by 4.

52. Use[latex]\text{ }f\left(x\right)={\mathrm{log}}_{4}\left(x\right)\text{ }[/latex]as the parent function.

The graph y=log_4(x) has been vertically stretched by 3, and shifted to the left by 2.

53. Use[latex]\text{ }f\left(x\right)={\mathrm{log}}_{5}\left(x\right)\text{ }[/latex]as the parent function.

The graph y=log_3(x) has been reflected over the x-axis and y-axis, vertically stretched by 2, and shifted to the right by 5.

Technology

For the following exercises, use a graphing calculator to find approximate solutions to each equation.

54. [latex]\mathrm{log}\left(x-1\right)+2=\mathrm{ln}\left(x-1\right)+2[/latex]

55. [latex]\mathrm{log}\left(2x-3\right)+2=-\mathrm{log}\left(2x-3\right)+5[/latex]

56. [latex]\mathrm{ln}\left(x-2\right)=-\mathrm{ln}\left(x+1\right)[/latex]

57. [latex]2\mathrm{ln}\left(5x+1\right)=\frac{1}{2}\mathrm{ln}\left(-5x\right)+1[/latex]

58. [latex]\frac{1}{3}\mathrm{log}\left(1-x\right)=\mathrm{log}\left(x+1\right)+\frac{1}{3}[/latex]

Extensions

59. Let[latex]\text{ }b\text{ }[/latex]be any positive real number such that[latex]\text{ }b\ne 1.\text{ }[/latex]What must[latex]\text{ }{\mathrm{log}}_{b}1\text{ }[/latex]be equal to? Verify the result.

60. Explore and discuss the graphs of[latex]\text{ }f\left(x\right)={\mathrm{log}}_{\frac{1}{2}}\left(x\right)\text{ }[/latex]and[latex]\text{ }g\left(x\right)=-{\mathrm{log}}_{2}\left(x\right).\text{ }[/latex]Make a conjecture based on the result.

61. Prove the conjecture made in the previous exercise.

62. What is the domain of the function[latex]\text{ }f\left(x\right)=\mathrm{ln}\left(\frac{x+2}{x-4}\right)?\text{ }[/latex]Discuss the result.

63. Use properties of exponents to find the x-intercepts of the function[latex]\text{ }f\left(x\right)=\mathrm{log}\left({x}^{2}+4x+4\right)\text{ }[/latex]algebraically. Show the steps for solving, and then verify the result by graphing the function.