3.1 Section Exercises

For Exercises 1-10, find the values of all six trigonometric functions of angles A and B in the right triangle △ ABC in Figure 8.

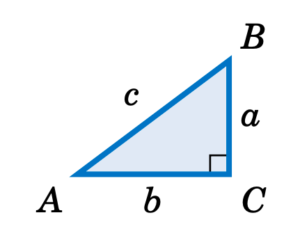
Figure 8. A right triangle with angles A B C and sides a b c

1. $$a = 5$$, $$b = 12$$, $$c = 13$$
2. $$a = 8$$, $$b = 15$$, $$c = 17$$
3. $$a = 7$$, $$b = 24$$, $$c = 25$$
4. $$a = 20$$, $$b = 21$$, $$c = 29$$
5. $$a = 9$$, $$b = 40$$, $$c = 41$$
6. $$a = 1$$, $$b = 2$$, $$c = \sqrt{5}$$
7. $$a = 1$$, $$b = 3$$
8. $$a = 2$$, $$b = 5$$
9. $$a = 5$$, $$c = 6$$
10. $$b = 7$$, $$c = 8$$

For Exercises 11-18, find the values of the other five trigonometric functions of the acute angle A given the indicated value of one of the functions.

11. $$\sin\;A = \frac{3}{4}$$
12. $$\cos\;A = \frac{2}{3}$$
13. $$\cos\;A = \frac{2}{\sqrt{10}}$$
14. $$\sin\;A = \frac{2}{4}$$
15. $$\tan\;A = \frac{5}{9}$$
16. $$\tan\;A = 3$$
17. $$\sec\;A = \frac{7}{3}$$
18. $$\csc\;A = 3$$

For Exercises 19-23, write the given number as a trigonometric function of an acute angle less than 45° .

19. $$\sin\;87^\circ$$
20. $$\sin\;53^\circ$$
21. $$\cos\;46^\circ$$
22. $$\tan\;66^\circ$$
23. $$\sec\;77^\circ$$

For Exercises 24-28, write the given number as a trigonometric function of an acute angle greater than 45$$^\circ$$ .

24. $$\sin\;1^\circ$$
25. $$\cos\;13^\circ$$
26. $$\tan\;26^\circ$$
27. $$\cot\;10^\circ$$
28. $$\csc\;43^\circ$$
29. In Example 1.7 we found the values of all six trigonometric functions of 60° and 30° .
    1. Does $$\;\sin\;30^\circ ~+~ \sin\;30^\circ ~=~ \sin\;60^\circ$$?
    2. Does $$\;\cos\;30^\circ ~+~ \cos\;30^\circ ~=~ \cos\;60^\circ$$?
    3. Does $$\;\tan\;30^\circ ~+~ \tan\;30^\circ ~=~ \tan\;60^\circ$$?
    4. Does $$\;2\,\sin\;30^\circ\,\cos\;30^\circ ~=~ \sin\;60^\circ$$?
30. For an acute angle $$A$$, can $$\sin\;A$$ be larger than $$1$$? Explain your answer.
31. For an acute angle $$A$$, can $$\cos\;A$$ be larger than $$1$$? Explain your answer.
32. For an acute angle $$A$$, can $$\sin\;A$$ be larger than $$\tan\;A$$? Explain your answer.
33. If $$A$$ and $$B$$ are acute angles and $$A < B$$, explain why $$\sin\;A < \sin\;B$$.
34. If $$A$$ and $$B$$ are acute angles and $$A < B$$, explain why $$\cos\;A > \cos\;B$$.
35. Prove the Cofunction Theorem. Hint: Draw a right triangle and label the angles and sides.