Finding the Average Rate of Change of a Function

The price change per year is a rate of change because it describes how an output quantity changes relative to the change in the input quantity. We can see that the price of gasoline in Table 1 did not change by the same amount each year, so the rate of change was not constant. If we use only the beginning and ending data, we would be finding the average rate of change over the specified period of time. To find the average rate of change, we divide the change in the output value by the change in the input value.

If we consider the two points [latex]\left({x}_{1}, {y}_{1}\right)[/latex] and [latex]\left({x}_{2}, {y}_{2}\right)[/latex] on the graph of a function [latex]f,[/latex] we can talk about the average rate of change on the interval of input values [latex]\left[{x}_{1}, {x}_{2}\right].[/latex]

The Greek letter [latex]\Delta[/latex] (delta) signifies the change in a quantity; we read the ratio as “delta-y over delta-x” or “the change in [latex]y[/latex] divided by the change in [latex]x.[/latex]” Occasionally we write [latex]\Delta f[/latex] instead of [latex]\Delta y,[/latex] which still represents the change in the function’s output value resulting from a change to its input value. It does not mean we are changing the function into some other function.

You may also see the interval given as [latex]\left[a,b\right].[/latex]  This means that our points would be [latex]\left(a, f\left(a\right)\right)[/latex] and [latex]\left(b, f\left(b\right)\right).[/latex] This would lead to the alternate form for the average rate of change shown below.

[latex]\begin{align*}\text{ Average rate of change }=\frac{f\left(b\right)-f\left(a\right)}{b-a}\end{align*}[/latex]

You should be comfortable working with any of these presentations of the material.

In our example, the gasoline price increased by $1.37 from 2005 to 2012. Over 7 years, the average rate of change was

On average, the price of gas increased by about 19.6¢ each year.

Other examples of rates of change include:

• A population of rats increasing by 40 rats per week
• A car traveling 68 miles per hour (distance traveled changes by 68 miles each hour as time passes)
• A car driving 27 miles per gallon (distance traveled changes by 27 miles for each gallon)
• The current through an electrical circuit increasing by 0.125 amperes for every volt of increased voltage
• The amount of money in a college account decreasing by $4,000 per quarter

[latex]\\[/latex]

Example 2:  Computing Average Rate of Change from a Graph

Given the function [latex]g\left(t\right)[/latex] shown in Figure 1, find the average rate of change on the interval [latex]\left[-1,2\right].[/latex]

Figure 1

Show Solution

At [latex]t=-1,[/latex] Figure 2 shows [latex]g\left(-1\right)=4.[/latex] At [latex]t=2,[/latex] the graph shows [latex]g\left(2\right)=1.[/latex]

Figure 2

The horizontal change [latex]\Delta t=3[/latex] is shown by the red arrow, and the vertical change [latex]\Delta g\left(t\right)=-3[/latex] is shown by the turquoise arrow. The output changes by –3 while the input changes by 3, giving an average rate of change of

[latex]\frac{1-4}{2-\left(-1\right)}=\frac{-3}{3}=-1[/latex]

Analysis

Note that the order we choose is very important. If, for example, we use [latex]\frac{{y}_{2}-{y}_{1}}{{x}_{1}-{x}_{2}},[/latex] we will not get the correct answer. Decide which point will be 1 and which point will be 2, and keep the coordinates fixed as [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right).[/latex]

Using a Graph to Determine Where a Function is Increasing, Decreasing, or Constant

As part of exploring how functions change, we can identify intervals over which the function is changing in specific ways. We say that a function is increasing on an interval if the function values increase as the input values increase within that interval. Similarly, a function is decreasing on an interval if the function values decrease as the input values increase over that interval.

The average rate of change of an increasing function is positive, and the average rate of change of a decreasing function is negative. Figure 3 shows examples of increasing and decreasing intervals on a function.

Figure 3 The function [latex]f\left(x\right)={x}^{3}-12x[/latex] is increasing on [latex]\left(-\infty \text{,}\text{ }-\text{2}\right){{\cup }^{\text{​}}}^{\text{​}}\left(2,\text{ }\infty \right)[/latex] and is decreasing on [latex]\left(-2\text{,}\text{ }2\right).[/latex]

While some functions are increasing (or decreasing) over their entire domain, many others are not. A value of the input where a function changes from increasing to decreasing (as we go from left to right, that is, as the input variable increases) is called a local maximum. If a function has more than one, we say it has local maxima. Similarly, a value of the input where a function changes from decreasing to increasing as the input variable increases is called a local minimum. The plural form is “local minima.” Together, local maxima and minima are called local extrema, or local extreme values, of the function. (The singular form is “extremum.”) Often, the term local is replaced by the term relative. In this text, we will use the term local.

Clearly, a function is neither increasing nor decreasing on an interval where it is constant. A function is also neither increasing nor decreasing at extrema. Note that we have to speak of local extrema, because any given local extremum as defined here is not necessarily the highest maximum or lowest minimum in the function’s entire domain.

For the function whose graph is shown in Figure 4, the local maximum occurs when [latex]x=-2[/latex]  The maximum value is the output value of 16.  The local minimum occurs when [latex]x=2[/latex] .  The minimum value is the output value of [latex]-16[/latex]

Figure 4

To locate the local maxima and minima from a graph, we need to observe the graph to determine where the graph attains its highest and lowest points, respectively, within an open interval. Like the summit of a roller coaster, the graph of a function is higher at a local maximum than at nearby points on both sides. The graph will also be lower at a local minimum than at neighboring points. Figure 5 illustrates these ideas for a local maximum.

Figure 5 Definition of a local maximum

These observations lead us to a formal definition of local extrema.

Example 7:  Finding Increasing and Decreasing Intervals on a Graph

Given the function [latex]p\left(t\right)[/latex] in Figure 6, identify the intervals on which the function appears to be increasing and decreasing.

Figure 6

Show Solution

We see that the function is not constant on any interval. The function is increasing where it slants upward as we move to the right and decreasing where it slants downward as we move to the right. The function appears to be increasing from [latex]t=1[/latex] to [latex]t=3[/latex] and from [latex]t=4[/latex] on. The function appears to be decreasing until [latex]t=1[/latex] and then again from [latex]t=3[/latex] to [latex]t=4.[/latex]

In interval notation, we would say the function appears to be increasing [latex]\left(1,\text{ }3\right)\cup\left(4,\infty \right)[/latex] and decreasing on [latex]\left(-\infty,\text{ }1\right)\cup\left(3,\text{ }4\right).[/latex]

Analysis

Notice in this example that we used open intervals (intervals that do not include the endpoints), because the function is neither increasing nor decreasing at [latex]t=1[/latex], [latex]t=3[/latex],  and [latex]t=4[/latex]. These points are the local extrema (two minima and a maximum).

Example 8:  Finding Local Extrema from a Graph

Use technology to graph the function [latex]f\left(x\right)=\frac{2}{x}+\frac{x}{3}.[/latex] Then use features of your graphing utility to estimate the local extrema of the function and to determine the intervals on which the function is increasing.

Show Solution

Using technology, we find that the graph of the function looks like that in Figure 7. It appears there is a low point, or local minimum, between [latex]x=2[/latex] and [latex]x=3,[/latex] and a mirror-image high point, or local maximum, somewhere between [latex]x=-3[/latex] and [latex]x=-2.[/latex]

Figure 7

Analysis

Most graphing calculators and graphing utilities can estimate the location of maxima and minima. Figure 8 provides screen images from two different technologies, showing the estimate for the local maximum and minimum.

Figure 8

Based on these estimates, the function is increasing on the interval [latex](-\infty \text{,}-\text{2}\text{.449)}[/latex] and [latex]\left(2.449\text{,}\infty \right).[/latex] Notice that, while we expect the extrema to be symmetric, the two different technologies agree only up to four decimals due to the differing approximation algorithms used by each. (The exact location of the extrema is at [latex]±\sqrt{6},[/latex] but determining this requires calculus.)

Example 9:  Finding Local Maxima and Minima from a Graph

For the function [latex]f[/latex] whose graph is shown in Figure 9, find all local maxima and minima.

Figure 9

Show Solution

Observe the graph of [latex]f.[/latex] The graph attains a local maximum at [latex]x=1[/latex] because the highest point in an open interval occurs when [latex]x=1.[/latex] The local maximum is the [latex]y[/latex]-coordinate at [latex]x=1,[/latex] which is [latex]2.[/latex]

The graph attains a local minimum at [latex]x=-1[/latex] because the lowest point in an open interval occurs when [latex]x=-1.[/latex] The local minimum is the y-coordinate at [latex]x=-1,[/latex] which is  [latex]-2.[/latex]

Analyzing the Toolkit Functions for Increasing or Decreasing Intervals

We will now return to our toolkit functions and discuss their graphical behavior in Figure 10, Figure 11, and Figure 12.

Figure 10

Figure 11

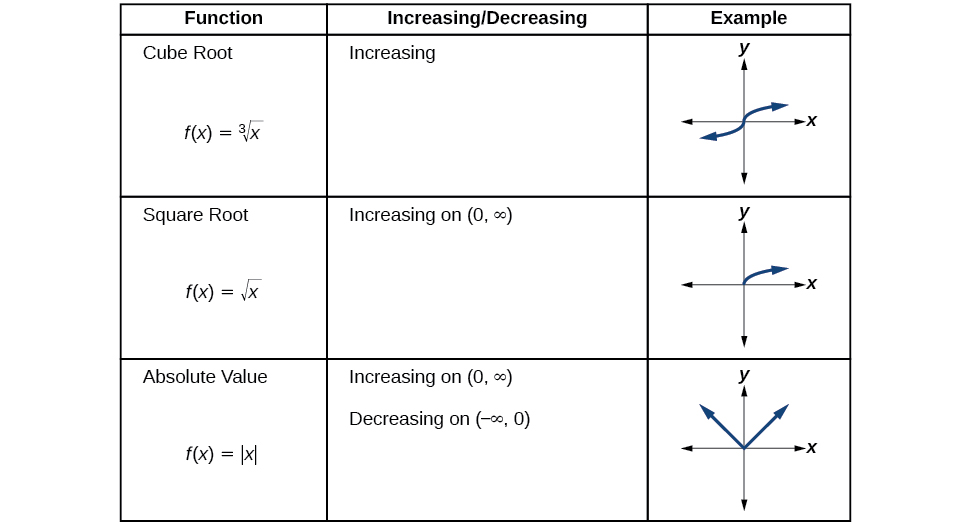
Figure 12

Use A Graph to Locate the Absolute Maximum and Absolute Minimum (Optional)

There is a difference between locating the highest and lowest points on a graph in a region around an open interval (locally) and locating the highest and lowest points on the graph for the entire domain. The [latex]y\text{-}[/latex]coordinates (output) at the highest and lowest points are called the absolute maximum and absolute minimum, respectively.

To locate absolute maxima and minima from a graph, we need to observe the graph to determine where the graph attains it highest and lowest points on the domain of the function. See Figure 13.

Figure 13

Not every function has an absolute maximum or minimum value. The toolkit function [latex]f\left(x\right)={x}^{3}[/latex] is one such function.

Example 10:  Finding Absolute Maxima and Minima from a Graph

For the function [latex]f[/latex] shown in Figure 14, find all absolute maxima and minima.

Figure 14

Show Solution

Observe the graph of [latex]f.[/latex] The graph attains an absolute maximum in two locations, [latex]x=-2[/latex] and [latex]x=2,[/latex] because at these locations, the graph attains its highest point on the domain of the function. The absolute maximum is the y-coordinate at [latex]x=-2[/latex] and [latex]x=2,[/latex] which is [latex]16.[/latex]

The graph attains an absolute minimum at [latex]x=3,[/latex] because it is the lowest point on the domain of the function’s graph. The absolute minimum is the y-coordinate at [latex]x=3,[/latex] which is [latex]-10.[/latex]