Consider a right triangle △ ABC, with the right angle at C and with lengths a, b, and c, as in the Figure 1 below. For the acute angle A, call the leg BC its opposite side, and call the leg AC its adjacent side. Recall that the hypotenuse of the triangle is always opposite the right angle.  In the triangle below, this is the side AB. The ratios of sides of a right triangle occur often enough in practical applications to warrant their own names, so we define the six trigonometric functions of A as follows:

Figure 1:  Sides of a right triangle with respect to angle A.

We will usually use the abbreviated names of the functions. Notice from Table 1 that the pairs sin(A) and csc(A), cos(A) and sec(A), and tan(A) and cot(A) are reciprocals:

Example 1:  Finding Trigonometric Functions Given Sides

For the right triangle △ ABC shown in Figure 2 below, find the values of all six trigonometric functions of the acute angles A and B.

 

 

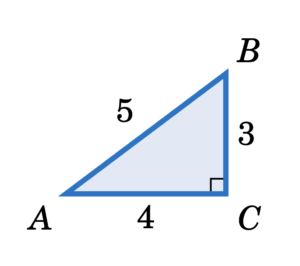
Figure 2: A Given Right Triangle

Show Solution

The hypotenuse of △ ABC has length 5. For angle A, the opposite side BC has length 3 and the adjacent side AC has length 4. Thus:

[latex]\sin\left(A\right) =\frac{Opposite}{Hypotenuse}=\frac{3}{5}[/latex]	[latex]\cos\left(A\right) =\frac{Adjacent}{Hypotenuse}=\frac{4}{5}[/latex]	[latex]\tan\left(A\right) =\frac{Opposite}{Adjacent}=\frac{3}{4}[/latex]
[latex]\csc\left(A\right) =\frac{Hypotenuse}{Opposite}=\frac{5}{3}[/latex]	[latex]\sec\left(A\right) =\frac{Hypotenuse}{Adjacent}=\frac{5}{4}[/latex]	[latex]\cot\left(A\right) =\frac{Adjacent}{Opposite}=\frac{4}{3}[/latex]

For angle B, the opposite side AC has length 4 and the adjacent side BC has length 3. Thus:

[latex]\sin \left(B\right) =\frac{Opposite}{Hypotenuse}=\frac{4}{5}[/latex]	[latex]\cos\left(B\right) =\frac{Adjacent}{Hypotenuse}=\frac{3}{5}[/latex]	[latex]\tan\left(B\right) =\frac{Opposite}{Adjacent}=\frac{4}{3}[/latex]
[latex]\csc\left(B\right) =\frac{Hypotenuse}{Opposite}=\frac{5}{4}[/latex]	[latex]\sec\left(B\right) =\frac{Hypotenuse}{Adjacent}=\frac{5}{3}[/latex]	[latex]\cot\left(B\right)=\frac{Adjacent}{Opposite}=\frac{3}{4}[/latex]

Notice in Example 1 that we did not specify the units for the lengths. This raises the possibility that our answers depended on a triangle of a specific physical size. For example, suppose that two different students are reading this textbook: one in the United States and one in Germany. The American student thinks that the lengths 3, 4, and 5 in Example 1 are measured in inches, while the German student thinks that they are measured in centimeters. Since 1 in ≈ 2.54 cm, the students are using triangles of different physical sizes (see Figure 3 below, not drawn to scale).

Figure 3.  △ ABC ∼ △ A′B′C′ This figure shows two 3,4,5 triangles. The first triangle is a 3,4,5 triangle in inches, the second is a 3,4,5 triangle in centimeters. The third visual shows that these sides correspond to each other.

If the American triangle is △ ABC and the German triangle is △ A ′B ′C ′ , then we see from Figure 1 that △ ABC is similar to △ A ′B ′C ′, and hence the corresponding angles are equal and the ratios of the corresponding sides are equal. In fact, we know that common ratio: the sides of △ ABC are approximately 2.54 times longer than the corresponding sides of △ A ′B ′C ′. So when the American student calculates sin A and the German student calculates sin A ′, they get the same answer:

[latex]\Delta ABC\sim\Delta A'B'C'\Rightarrow \frac{BC}{B'C'}=\frac{AB}{A'B'}\Rightarrow \frac{BC}{AB}=\frac{B'C'}{A'B'}\Rightarrow \sin(A)=\sin(A')[/latex]

Likewise, the other values of the trigonometric functions of A and A ′ are the same. In fact, our argument was general enough to work with any similar right triangles. This leads us to the following conclusion:

Since we defined the trigonometric functions in terms of ratios of sides, you can think of the units of measurement for those sides as canceling out in those ratios. This means that the values of the trigonometric functions are unitless numbers. So when the American student calculated 3/5 as the value of sin(A) in Example 1, that is the same as the 3/5 that the German student calculated, despite the different units for the lengths of the sides.

Example 2:  Finding Trigonometric Values for a 45 Degree Angle

Find the values of all six trigonometric functions of 45º.

Figure 4. A 45°-45°-90° Right Triangle

Show Solution

Since we may use any right triangle which has 45º as one of the angles, use the simplest one: take a square whose sides are all 1 unit long and divide it in half diagonally, as in the figure on the right. Since the two legs of the triangle △ ABC have the same length, △ ABC is an isosceles triangle, which means that the angles A and B are equal. So since A + B = 90º , this means that we must have A = B = 45º . By the Pythagorean Theorem, the length c of the hypotenuse is given by

[latex]{{c}^{2}}={{1}^{2}}+{{1}^{2}}=2\Rightarrow c=\sqrt[\leftroot{1}\uproot{2} ]{2}[/latex]

Thus, using the angle A we get:

[latex]\sin {\left({45}^{\circ }\right)}=\frac{Opposite}{Hypotenuse}=\frac{1}{\sqrt[\leftroot{1}\uproot{2} ]{2}}[/latex]	[latex]\cos{\left({45}^{\circ }\right)}=\frac{Adjacent}{Hypotenuse}=\frac{1}{\sqrt[\leftroot{1}\uproot{2} ]{2}}[/latex]	[latex]\tan{\left({45}^{\circ }\right)}=\frac{Opposite}{Adjacent}=\frac{1}{1}={1}[/latex]
[latex]\csc{\left({45}^{\circ }\right)}=\frac{Hypotenuse}{Opposite}=\sqrt[\leftroot{1}\uproot{2} ]{2}[/latex]	[latex]\sec{\left({45}^{\circ }\right)}=\frac{Hypotenuse}{Adjacent}=\sqrt[\leftroot{1}\uproot{2} ]{2}[/latex]	[latex]\cot{\left({45}^{\circ }\right)}=\frac{Adjacent}{Opposite}=\frac{1}{1}={1}[/latex]

Note that we would have obtained the same answers if we had used any right triangle similar to △ ABC. For example, if we multiply each side of △ ABC by [latex]\sqrt[\leftroot{1}\uproot{2}]{2}[/latex], then we would have a similar triangle with legs of length [latex]\sqrt[\leftroot{1}\uproot{2}]{2}[/latex] and hypotenuse of length 2. This would give us [latex]\mathrm{sin}\left(45^{\circ }\right)=\frac{\sqrt[\leftroot{1}\uproot{2}]{2}}{2}[/latex] , which equals [latex]\frac{\sqrt[\leftroot{1}\uproot{2}]{2}}{\sqrt[\leftroot{1}\uproot{2}]{2}\cdot\sqrt[\leftroot{1}\uproot{2}]{2}}=\frac{1}{\sqrt[\leftroot{1}\uproot{2}]{2}}[/latex] as before. The same goes for the other functions.

Example 3:  Finding Trigonometric Values for 30 and 60 Degree Angles

Find the values of all six trigonometric functions of 60º.

Figure 5. A 30°-60°-90° Right Triangle

Show Solution

Since we may use any right triangle which has 60º as one of the angles, we will use a simple one: take a triangle whose sides are all 2 units long and divide it in half by drawing the bisector from one vertex to the opposite side, as in the figure above. Since the original triangle was an equilateral triangle (i.e. all three sides had the same length), its three angles were all the same, namely 60º . Recall from elementary geometry that the bisector from the vertex angle of an equilateral triangle to its opposite side bisects both the vertex angle and the opposite side. So as in Figure 5 shown, the triangle △ ABC has angle A = 60º and angle B = 30º , which forces the angle C to be 90º . Thus, △ ABC is a right triangle. We see that the hypotenuse has length c = AB = 2 and the leg AC has length b = AC = 1. By the Pythagorean Theorem, the length a of the leg BC is given by

[latex]{{a}^{2}}+{{b}^{2}}={{c}^{2}}\Rightarrow {{a}^{2}}={{2}^{2}}-{{1}^{2}}=3\Rightarrow a=\sqrt[\leftroot{1}\uproot{2}]{3}[/latex]

Thus, using the angle A we get:

[latex]\sin \left({{60}^{\circ }}\right) =\frac{Opposite}{Hypotenuse}=\frac{\sqrt[\leftroot{1}\uproot{2} ]{3}}{2}[/latex]	[latex]\cos\left({{60}^{\circ }}\right) =\frac{Adjacent}{Hypotenuse}=\frac{1}{2}[/latex]	[latex]\tan\left({{60}^{\circ }}\right) =\frac{Opposite}{Adjacent}=\frac{\sqrt[\leftroot{1}\uproot{2}]{3}}{1}={\sqrt{3}}[/latex]
[latex]\csc\left({{60}^{\circ }}\right) =\frac{Hypotenuse}{Opposite}=\frac{2}{\sqrt[\leftroot{1}\uproot{2}]{3}}[/latex]	[latex]\sec\left({{60}^{\circ }}\right) =\frac{Hypotenuse}{Adjacent}={2}[/latex]	[latex]\cot\left({{60}^{\circ }}\right) =\frac{Adjacent}{Opposite}=\frac{1}{\sqrt[\leftroot{1}\uproot{2}]{3}}[/latex]

Notice that, as a bonus, we get the values of all six trigonometric functions of 30º , by using angle B = 30º in the same triangle △ ABC above:

[latex]\sin\left({{30}^{\circ }}\right) =\frac{Opposite}{Hypotenuse}=\frac{1}{2}[/latex]	[latex]\cos\left({{30}^{\circ }}\right) =\frac{Adjacent}{Hypotenuse}=\frac{\sqrt[\leftroot{1}\uproot{2}]{3}}{2}[/latex]	[latex]\tan\left({{30}^{\circ }}\right) =\frac{Opposite}{Adjacent}=\frac{1}{\sqrt[\leftroot{1}\uproot{2}]{3}}[/latex]
[latex]\csc\left({{30}^{\circ }}\right) =\frac{Hypotenuse}{Opposite}={2}[/latex]	[latex]\sec\left({{30}^{\circ }}\right) =\frac{Hypotenuse}{Adjacent}=\frac{2}{\sqrt[\leftroot{1}\uproot{2}]{3}}[/latex]	[latex]\cot\left({{30}^{\circ }}\right) =\frac{Adjacent}{opposite}=\frac{\sqrt[\leftroot{1}\uproot{2}]{3}}{1}={\sqrt{3}}[/latex]

Figure 6: Two general right triangles (any a > 0)

The angles 30º , 45º , and 60º arise often in applications. We can see what any 45º− 45º−90º and 30º−60º−90º right triangles look like, as in Figure 6 above.  Notice that the sides can now be any length that fits these ratios, and not just the sides of [latex]1-2-\sqrt{3}\text{ or }1-1-\sqrt[\leftroot{1}\uproot{2}]{2}.[/latex]  For example, the sides of a 30º−60º−90º right triangle might be [latex]4 - 8 - 4\sqrt[\leftroot{1}\uproot{2}]{3}.[/latex]

Example 4:  Given One Trigonometric Value, Find Remaining Values

A is an acute angle such that [latex]\sin\left({A}\right)=\frac{2}{3}[/latex] . Find the values of the other trigonometric functions of A.

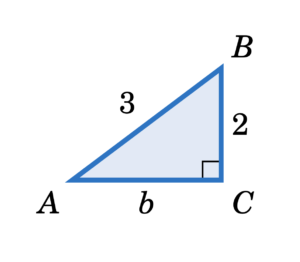
Figure 6. A right triangle where [latex]\sin\left(A\right)=\frac{2}{3}[/latex]

Show Solution

In general it helps to draw a right triangle to solve problems of this type. The reason is that the trigonometric functions were defined in terms of ratios of sides of a right triangle, and you are given one such function (the sine, in this case) already in terms of a ratio: [latex]\sin\left({A}\right)=\frac{2}{3}[/latex] . Since sin(A) is defined as [latex]\frac{opposite}{hypotenuse}[/latex], use 2 as the length of the side opposite A and use 3 as the length of the hypotenuse in a right triangle △ ABC as shown in Figure 6, so that [latex]\sin\left({A}\right)=\frac{2}{3}[/latex] . The adjacent side to A has unknown length b, but we can use the Pythagorean Theorem to find it:

[latex]{{2}^{2}}+{{b}^{2}}={{3}^{2}}\Rightarrow {{b}^{2}}=9-4=5\Rightarrow b=\sqrt[\leftroot{1}\uproot{2}]{5}[/latex]

We now know the lengths of all sides of the triangle △ ABC, so we have:

[latex]\cos \left(A\right)=\frac{Adjacent}{Hypotenuse}=\frac{\sqrt[\leftroot{1}\uproot{2}]{5}}{3}[/latex]

[latex]\tan\left(A\right)=\frac{Opposite}{Adjacent}=\frac{2}{\sqrt[\leftroot{1}\uproot{2}]{5}}[/latex]

[latex]\csc\left(A\right)=\frac{Hypotenuse}{Opposite}=\frac{3}{2}[/latex]

[latex]\sec\left(A\right)=\frac{Hypotenuse}{Adjacent}=\frac{3}{\sqrt[\leftroot{1}\uproot{2}]{5}}[/latex]

[latex]\cot\left(A\right)=\frac{Adjacent}{Opposite}=\frac{\sqrt[\leftroot{1}\uproot{2}]{5}}{2}[/latex]

You may have noticed the connections between the sine and cosine, secant and cosecant, and tangent and cotangent of the complementary angles in Examples 3 and 4. Generalizing those examples gives us the following theorem:

So sine and cosine are cofunctions, secant and cosecant are cofunctions, and tangent and cotangent are cofunctions. That is how the functions cosine, cosecant, and cotangent got the “co” in their names. The Cofunction Theorem says that any trigonometric function of an acute angle is equal to its co-function of the complementary angle.