8.3 The Ideal Gas Law

Learning Objectives

By the end of this section, you will be able to:

Use the ideal gas law, and related gas laws, to compute the values of various gas properties under specified conditions

The Ideal Gas Law

To this point, four separate laws have been discussed that relate pressure, volume, temperature, and the number of moles of the gas:

Boyle’s law: PV = constant at constant T and n
Gay-Lussac’s law: [latex]\large\frac{P}{T}[/latex] = constant at constant V and n
Charles’s law: [latex]\large\frac{V}{T}[/latex] = constant at constant P and n
Avogadro’s law: [latex]\large\frac{V}{n}[/latex] = constant at constant P and T

Combining these four laws yields the ideal gas law, a relation between the pressure, volume, temperature, and number of moles of a gas:

[latex]\large PV=nRT[/latex]

where P is the pressure of a gas, V is its volume, n is the number of moles of the gas, T is its temperature on the kelvin scale, and R is a constant called the ideal gas constant or the universal gas constant. The units used to express pressure, volume, and temperature will determine the proper form of the gas constant as required by dimensional analysis, the most commonly encountered values being 0.08206 L atm mol^–1 K^–1 and 8.314 J L mol^–1 K^–1.

Gases whose properties of P, V, and T are accurately described by the ideal gas law (or the other gas laws) are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter. Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures.

The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit use of the ideal gas law to calculate the fifth term as demonstrated in the following example exercises.

Example 1: Using the Ideal Gas Law

Methane, CH₄, is being considered for use as an alternative automotive fuel to replace gasoline. One gallon of gasoline could be replaced by 655 g of CH₄. What is the volume of this much methane at 25 °C and 745 torr?

Show Answer

Check Your Learning

Calculate the pressure in bar of 2520 moles of hydrogen gas stored at 27 °C in the 180-L storage tank of a modern hydrogen-powered car.

Show Answer

Standard Conditions of Temperature and Pressure

We have seen that the volume of a given quantity of gas and the number of molecules (moles) in a given volume of gas vary with changes in pressure and temperature. Chemists sometimes make comparisons against a standard temperature and pressure (STP) for reporting properties of gases: 273.15 K and 1 atm (101.325 kPa). At STP, an ideal gas has a volume of about 22.4 L—this is referred to as the standard molar volume (Figure 10).

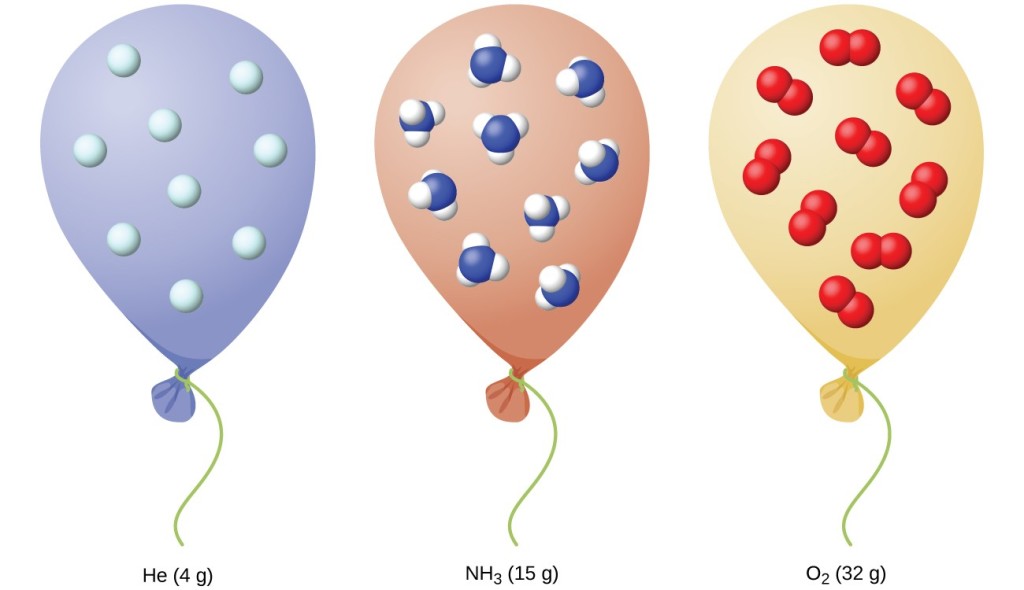
This figure shows three balloons each filled with H e, N H subscript 2, and O subscript 2 respectively. Beneath the first balloon is the label “4 g of He” Beneath the second balloon is the label, “15 g of N H subscript 2.” Beneath the third balloon is the label “32 g of O subscript 2.” Each balloon contains the same number of molecules of their respective gases.

Figure 1. Since the number of moles in a given volume of gas varies with pressure and temperature changes, chemists use standard temperature and pressure (273.15 K and 1 atm or 101.325 kPa) to report properties of gases.

Key Concepts and Summary

The equations describing these laws are special cases of the ideal gas law, PV = nRT, where P is the pressure of the gas, V is its volume, n is the number of moles of the gas, T is its kelvin temperature, and R is the ideal (universal) gas constant.

Key Equations

PV = nRT

Exercises

A weather balloon contains 8.80 moles of helium at a pressure of 0.992 atm and a temperature of 25 °C at ground level. What is the volume of the balloon under these conditions?
The volume of an automobile air bag was 66.8 L when inflated at 25 °C with 77.8 g of nitrogen gas. What was the pressure in the bag in kPa?
How many moles of gaseous boron trifluoride, BF₃, are contained in a 4.3410 L bulb at 788.0 K if the pressure is 1.220 atm? How many grams of BF₃?
Iodine, I₂, is a solid at room temperature but sublimes (converts from a solid into a gas) when warmed. What is the temperature in a 73.3 mL bulb that contains 0.292 g of I₂ vapor at a pressure of 0.462 atm?
How many grams of gas are present in each of the following cases?
1. 0.100 L of CO₂ at 307 torr and 26 °C
2. 8.75 L of C₂H₄, at 378.3 kPa and 483 K
3. 221 mL of Ar at 0.23 torr and –54 °C
A high altitude balloon is filled with 1.41 × 10⁴ L of hydrogen at a temperature of 21 °C and a pressure of 745 torr. What is the volume of the balloon at a height of 20 km, where the temperature is –48 °C and the pressure is 63.1 torr?
A cylinder of medical oxygen has a volume of 35.4 L, and contains O₂ at a pressure of 151 atm and a temperature of 25 °C. What volume of O₂ does this correspond to at normal body conditions, that is, 1 atm and 37 °C?
A large scuba tank (Figure 8) with a volume of 18 L is rated for a pressure of 220 bar. The tank is filled at 20 °C and contains enough air to supply 1860 L of air to a diver at a pressure of 2.37 atm (a depth of 45 feet). Was the tank filled to capacity at 20 °C?
A 20.0 L cylinder containing 11.34 kg of butane, C₄H₁₀, was opened to the atmosphere. Calculate the mass of the gas remaining in the cylinder if it were opened and the gas escaped until the pressure in the cylinder was equal to the atmospheric pressure, 0.983 atm, and a temperature of 27 °C.
While resting, the average 70 kg human male consumes 14 L of pure O₂ per hour at 25 °C and 100 kPa. How many moles of O₂ are consumed by a 70 kg man while resting for 1.0 h?
A liter of methane gas, CH₄, at STP contains more atoms of hydrogen than does a liter of pure hydrogen gas, H₂, at STP. Using Avogadro’s law as a starting point, explain why.
The effect of chlorofluorocarbons (such as CCl₂F₂) on the depletion of the ozone layer is well known. The use of substitutes, such as CH₃CH₂F(g), for the chlorofluorocarbons, has largely corrected the problem. Calculate the volume occupied by 10.0 g of each of these compounds at STP:
1. CCl₂F₂(g)
2. CH₃CH₂F(g)

Selected Answers

1. PV = nRT

[latex]V=\frac{nRT}{P}=\frac{8.80\cancel{\text{mol}}\times 0.08206\text{ L}\cancel{\text{atm}}{\cancel{\text{mol}}}^{{-1}}\cancel{{\text{K}}^{{-1}}}\times 298.15\cancel{\text{K}}}{0.992\cancel{\text{atm}}}=217\text{ L}[/latex]

3. [latex]n=\frac{PV}{RT}\frac{1.220\cancel{\text{atm}}\left(4.3410\text{L}\right)}{\left(0.08206\text{L}\cancel{\text{atm}}\text{ mol}{{-1}}^{}\cancel{{\text{K}}^{{-1}}}\right)\left(788.0\cancel{\text{K}}\right)}=0.08190\text{mol}=8.190\times {10}^{{-2}}\text{mol}[/latex]

[latex]n\times \text{molar mass}=8.190\times {10}^{{-2}}\cancel{\text{mol}}\times 67.8052\text{g}{\cancel{\text{mol}}}^{{-1}}=5.553\text{g}[/latex]

5. In each of these problems, we are given a volume, pressure, and temperature. We can obtain moles from this information using the molar mass, m = nℳ, where ℳ is the molar mass:

[latex]P,V,T\,\,\,{\xrightarrow{n=PV\text{/}RT}}\,\,\,n,\,\,\,{\xrightarrow{m=n\left(\text{molar mass}\right)}}\,\,\,\text{grams}[/latex]

or we can combine these equations to obtain:

[latex]\text{mass}=m=\frac{PV}{RT}\times[/latex]ℳ

[latex]\begin{array}{l}\\307\cancel{\text{torr}}\times \frac{1\text{atm}}{760\cancel{\text{torr}}}=0.4039\text{ atm }25^\circ{\text{ C}}=299.1 \text{ K}\\ \text{Mass}=m=\frac{0.4039\cancel{\text{atm}}\left(0.100\cancel{\text{L}}\right)}{0.08206\cancel{\text{L}}\cancel{\text{atm}}{\text{mol}}^{{-1}}\cancel{{\text{K}}^{{-1}}}\left(299.1\cancel{\text{K}}\right)}\times 44.01\text{g}{\text{mol}}^{{-1}}=7.24\times {10}^{{-2}}\text{g}\end{array}[/latex]
[latex]\text{Mass}=m=\frac{378.3\cancel{\text{kPa}}\left(8.75\cancel{\text{L}}\right)}{8.314\cancel{\text{L}}\cancel{\text{kPa}}{\text{mol}}^{{-1}}\cancel{{\text{K}}^{{-1}}}\left(483\cancel{\text{K}}\right)}\times 28.05376\text{ g}{\text{mol}}^{{-1}}=23.1\text{g}[/latex]
[latex]\begin{array}{l}\\ \\ 221\cancel{\text{mL}}\times \frac{1\text{L}}{1000\cancel{\text{mL}}}=0.221\text{L}-54^{\circ}\text{C}+273.15=219.15\text{K}\\ 0.23\cancel{\text{torr}}\times \frac{1\text{atm}}{760\cancel{\text{torr}}}=3.03\times {10}^{{-4}}\text{atm}\\ \text{Mass}=m=\frac{3.03\times {10}^{{-4}}\cancel{\text{atm}}\left(0.221\cancel{\text{L}}\right)}{0.08206\cancel{\text{L}}\cancel{\text{atm}}{\text{mol}}^{{-1}}\cancel{{\text{K}}^{{-1}}}\left(219.15\cancel{\text{K}}\right)}\times 39.978\text{ g}{\text{mol}}^{{-1}}=1.5\times {10}^{{-4}}\text{g}\end{array}[/latex]

7. [latex]\frac{{P}_{2}}{{T}_{2}}=\frac{{P}_{1}}{{T}_{1}}[/latex]

T₂ = 49.5 + 273.15 = 322.65 K

[latex]{P}_{2}=\frac{{P}_{1}{T}_{2}}{{T}_{1}}=149.6\text{atm}\times \frac{322.65}{278.15}=173.5\text{ atm}[/latex]

9. Calculate the amount of butane in 20.0 L at 0.983 atm and 27°C. The original amount in the container does not matter. [latex]n=\frac{PV}{RT}=\frac{0.983\cancel{\text{atm}}\times 20.0\cancel{\text{L}}}{0.08206\cancel{\text{L}}\cancel{\text{atm}}{\text{mol}}^{{-1}}\cancel{{\text{K}}^{{-1}}}\left(300.1\cancel{\text{K}}\right)}=0.798\text{mol}[/latex] Mass of butane = 0.798 mol × 58.1234 g/mol = 46.4 g

12. The volume is as follows:

Determine the molar mass of CCl₂F₂ then calculate the moles of CCl₂F₂(g) present. Use the ideal gas law PV = nRT to calculate the volume of CCl₂F₂(g):
[latex]\text{10.0 g }{\text{CCl}}_{2}{\text{F}}_{2}\times \frac{1\text{ mol}{\text{CC1}}_{2}{\text{F}}_{2}}{120.91\text{ g }{\text{CCl}}_{2}{\text{F}}_{2}}=0.0827\text{ mol }{\text{CCl}}_{2}{\text{F}}_{2}[/latex]
PV = nRT, where n = # mol CCl₂F₂[latex]1\text{ atm }\times V=0.0827\text{ mol }\times \frac{0.0821\text{ L atm}}{\text{mol K}}\times 273\text{ K}=1.85\text{ L }{\text{CCl}}_{2}{\text{F}}_{2};[/latex]
[latex]10.0\text{ g }{\text{CH}}_{3}{\text{CH}}_{2}\text{F}\times \frac{1\text{ mol }{\text{CH}}_{3}{\text{CH}}_{2}\text{F}}{48.07{\text{ g CH}}_{3}{\text{CH}}_{2}\text{F}}=0.208\text{ mol }{\text{CH}}_{3}{\text{CH}}_{2}\text{F}[/latex]
PV = nRT, with n = # mol CH₃CH₂F
1 atm × V = 0.208 mol × 0.0821 L atm/mol K × 273 K = 4.66 L CH₃ CH₂ F

Glossary

ideal gas: hypothetical gas whose physical properties are perfectly described by the gas laws

ideal gas constant (R): constant derived from the ideal gas equation R = 0.08226 L atm mol^–1 K^–1 or 8.314 L kPa mol^–1 K^–1

ideal gas law: relation between the pressure, volume, amount, and temperature of a gas under conditions derived by combination of the simple gas laws

standard conditions of temperature and pressure (STP): 273.15 K (0 °C) and 1 atm (101.325 kPa)

standard molar volume: volume of 1 mole of gas at STP, approximately 22.4 L for gases behaving ideally

Chapter 8. Gases