6.3 Molecular Shape

Learning Objectives

By the end of this section, you will be able to:

  • Predict the structures of small molecules using valence shell electron pair repulsion (VSEPR) theory

Thus far, we have used two-dimensional Lewis structures to represent molecules. However, molecular structure is actually three-dimensional, and it is important to be able to describe molecular bonds in terms of their distances, angles, and relative arrangements in space (Figure 1). A bond angle is the angle between any two bonds that include a common atom, usually measured in degrees. A bond distance (or bond length) is the distance between the nuclei of two bonded atoms along the straight line joining the nuclei. Bond distances are measured in Ångstroms (1 Å = 10–10 m) or picometers (1 pm = 10–12 m, 100 pm = 1 Å).

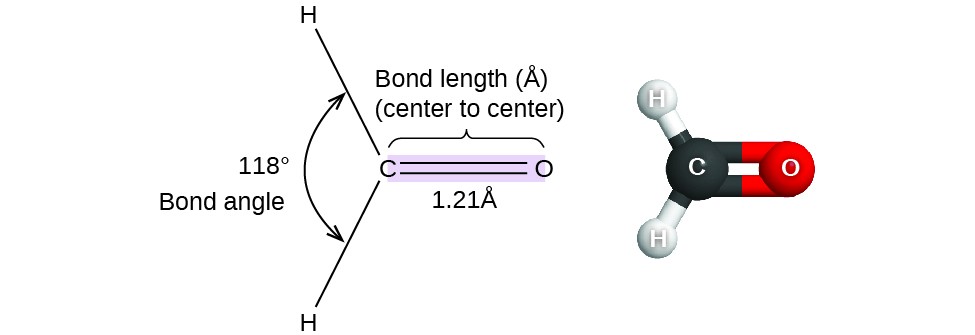
A pair of images are shown. The left image shows a carbon atom with three atoms bonded in a triangular arrangement around it. There are two hydrogen atoms bonded on the left side of the carbon and the angle between them is labeled, “118 degrees” and, “Bond angle.” The carbon is also double bonded to an oxygen atom. The double bond is shaded and there is a bracket which labels the bond, “Bond length ( angstrom ), ( center to center ),” and, “1.21 angstrom.” The right image shows a ball-and-stick model of the same elements. The hydrogen atoms are white, the carbon atom is black, and the oxygen atom is red.

Figure 1. Bond distances (lengths) and angles are shown for the formaldehyde molecule, H2CO.

VSEPR Theory

Valence shell electron-pair repulsion theory (VSEPR theory) enables us to predict the molecular structure, including approximate bond angles around a central atom, of a molecule from an examination of the number of bonds and lone electron pairs in its Lewis structure. The VSEPR model assumes that electron pairs in the valence shell of a central atom will adopt an arrangement that minimizes repulsions between these electron pairs by maximizing the distance between them. The electrons in the valence shell of a central atom form either bonding pairs of electrons, located primarily between bonded atoms, or lone pairs. The electrostatic repulsion of these electrons is reduced when the various regions of high electron density assume positions as far from each other as possible.

VSEPR theory predicts the arrangement of electron pairs around each central atom and, usually, the correct arrangement of atoms in a molecule. We should understand, however, that the theory only considers electron-pair repulsions. Other interactions, such as nuclear-nuclear repulsions and nuclear-electron attractions, are also involved in the final arrangement that atoms adopt in a particular molecular structure.

As a simple example of VSEPR theory, let us predict the structure of a gaseous CO2 molecule. The Lewis structure of CO2 (Figure 2) shows only two electron pairs around the central carbon atom. With two bonds and no lone pairs of electrons on the central atom, the bonds are as far apart as possible, and the electrostatic repulsion between these regions of high electron density is reduced to a minimum when they are on opposite sides of the central atom. The bond angle is 180° (Figure 2). Figure 3 illustrates this and other electron-pair geometries that minimize the repulsions among regions of high electron density (bonds and/or lone pairs). Two regions of electron density around a central atom in a molecule form a linear geometry; three regions form a trigonal planar geometry; four regions form a tetrahedral geometry; five regions form a trigonal bipyramidal geometry; and six regions form an octahedral geometry.

Figure 2. Carbon dioxide adopts a linear structure in which the two bonds are as far apart as possible, on opposite sides of the C atom

 

Figure 3 Basic electron-pair geometries predicted by VSEPR theory maximize the space around any region of electron density (bonds or lone pairs).

Electron-Pair Geometry versus Molecular Structure

It is important to note that electron-pair geometry around a central atom is not the same thing as its molecular structure. The electron-pair geometries shown in Figure 3 describe all regions where electrons are located, bonds as well as lone pairs. Molecular structure describes the location of the atoms, not the electrons.

A Lewis structure shows a carbon atom single bonded to four hydrogen atoms. This structure uses wedges and dashes to give it a three dimensional appearance.

Figure 4. The molecular structure of the methane molecule, CH4, is shown with a tetrahedral arrangement of the hydrogen atoms.

We differentiate between these two situations by naming the geometry that includes all electron pairs the electron-pair geometry. The structure that includes only the placement of the atoms in the molecule is called the molecular structure. The electron-pair geometries will be the same as the molecular structures when there are no lone electron pairs around the central atom, but they will be different when there are lone pairs present on the central atom.

VSEPR structures like the one in Figure 4 are often drawn using the wedge and dash notation, in which solid lines represent bonds in the plane of the page, solid wedges represent bonds coming up out of the plane, and dashed lines represent bonds going down into the plane. For example, the methane molecule, CH4, which is the major component of natural gas, has four bonding pairs of electrons around the central carbon atom; the electron-pair geometry is tetrahedral, as is the molecular structure (Figure 4). On the other hand, the ammonia molecule, NH3, also has four electron pairs associated with the nitrogen atom, and thus has a tetrahedral electron-pair geometry. One of these regions, however, is a lone pair, which is not included in the molecular structure, and this lone pair influences the shape of the molecule (Figure 5).

Three images are shown and labeled, “a,” “b,” and “c.” Image a shows a nitrogen atom single bonded to three hydrogen atoms. There are four oval-shaped orbs that surround each hydrogen and one facing away from the rest of the molecule. These orbs are located in a tetrahedral arrangement. Image b shows a ball-and-stick model of the nitrogen single bonded to the three hydrogen atoms. Image c is the same as image a, but there are four curved, double headed arrows that circle the molecule and are labeled, “106.8 degrees.”

Figure 5. (a) The electron-pair geometry for the ammonia molecule is tetrahedral with one lone pair and three single bonds. (b) The trigonal pyramidal molecular structure is determined from the electron-pair geometry. (c) The actual bond angles deviate slightly from the idealized angles, because the lone pair takes up a larger region of space than do the single bonds, causing the HNH angle to be slightly smaller than 109.5°.

As seen in Figure 5, small distortions from the ideal angles in Figure 6 can result from differences in repulsion between various regions of electron density. VSEPR theory predicts these distortions by establishing an order of repulsions and an order of the amount of space occupied by different kinds of electron pairs. The order of electron-pair repulsions from greatest to least repulsion is:

lone pair-lone pair > lone pair-bonding pair > bonding pair-bonding pair

This order of repulsions determines the amount of space occupied by different regions of electrons. A lone pair of electrons occupies a larger region of space than the electrons in a triple bond; in turn, electrons in a triple bond occupy more space than those in a double bond, and so on. The order of sizes from largest to smallest is:

lone pair > triple bond > double bond>single bond

Consider formaldehyde, H2CO, which is used as a preservative for biological and anatomical specimens (Figure 1). This molecule has regions of high electron density that consist of two single bonds and one double bond. The basic geometry is trigonal planar with 120° bond angles, but we see that the double bond causes slightly larger angles (121°), and the angle between the single bonds is slightly smaller (118°).

In the ammonia molecule, the three hydrogen atoms attached to the central nitrogen are not arranged in a flat, trigonal planar molecular structure, but rather in a three-dimensional trigonal pyramid (Figure 5) with the nitrogen atom at the apex and the three hydrogen atoms forming the base. The ideal bond angles in a trigonal pyramid are based on the tetrahedral electron pair geometry. Again, there are slight deviations from the ideal because lone pairs occupy larger regions of space than do bonding electrons. The H–N–H bond angles in NH3 are slightly smaller than the 109.5° angle in a regular tetrahedron (Figure 3) because the lone pair-bonding pair repulsion is greater than the bonding pair-bonding pair repulsion (Figure 5). Figure 6 illustrates the ideal molecular structures, which are predicted based on the electron-pair geometries for various combinations of lone pairs and bonding pairs.

Figure 6. The molecular structures are identical to the electron-pair geometries when there are no lone pairs present (first column). For a particular number of electron pairs (row), the molecular structures for one or more lone pairs are determined based on modifications of the corresponding electron-pair geometry.

According to VSEPR theory, the terminal atom locations (Xs in Figure 6) are equivalent within the linear, trigonal planar, and tetrahedral electron-pair geometries (the first three rows of the table). It does not matter which X is replaced with a lone pair, because the molecules can be rotated to convert positions.

Predicting Electron Pair Geometry and Molecular Structure

The following procedure uses VSEPR theory to determine the electron pair geometries and the molecular structures:

  1. Write the Lewis structure of the molecule or polyatomic ion.
  2. Count the number of regions of electron density (lone pairs and bonds) around the central atom. A single, double, or triple bond counts as one region of electron density.
  3. Identify the electron-pair geometry based on the number of regions of electron density: linear, trigonal planar, or tetrahedral. (Figure 6, first column).
  4. Use the number of lone pairs to determine the molecular structure (Figure 6). If more than one arrangement of lone pairs and chemical bonds is possible, choose the one that will minimize repulsions, remembering that lone pairs occupy more space than multiple bonds, which occupy more space than single bonds.

The following examples illustrate the use of VSEPR theory to predict the molecular structure of molecules or ions that have no lone pairs of electrons. In this case, the molecular structure is identical to the electron pair geometry.

Example 1: Predicting Electron-pair Geometry and Molecular Structure

Predict the electron-pair geometry and molecular structure for phosgene, COCl2, a chemical warfare agent used during World War I

The next several examples illustrate the effect of lone pairs of electrons on molecular structure.

Example 2: Predicting Electron-pair Geometry and Molecular Structure: Lone Pairs on the Central Atom

Predict the electron-pair geometry and molecular structure of a water molecule.

Example 3: Molecular Simulation

Using molecular shape simulator allows us to control whether bond angles and/or lone pairs are displayed by checking or unchecking the boxes under “Options” on the right. We can also use the “Name” checkboxes at bottom-left to display or hide the electron pair geometry (called “electron geometry” in the simulator) and/or molecular structure (called “molecular shape” in the simulator).

Build the molecule HCN in the simulator based on the following Lewis structure:

[latex]\text{H-C}\equiv \text{N}[/latex]

Click on each bond type or lone pair at right to add that group to the central atom. Once you have the complete molecule, rotate it to examine the predicted molecular structure. What molecular structure is this?

Key Concepts and Summary

VSEPR theory predicts the three-dimensional arrangement of atoms in a molecule. It states that valence electrons will assume an electron-pair geometry that minimizes repulsions between areas of high electron density (bonds and/or lone pairs). Molecular structure, which refers only to the placement of atoms in a molecule and not the electrons, is equivalent to electron-pair geometry only when there are no lone electron pairs around the central atom.

Exercises

  1. Explain the difference between electron-pair geometry and molecular structure.
  2. Why is the H–N–H angle in NH3 smaller than the H–C–H bond angle in CH4? Why is the H–N–H angle in [latex]{\text{NH}}_{4}^{+}[/latex] identical to the H–C–H bond angle in CH4?
  3. Identify the electron pair geometry and the molecular structure of each of the following molecules:
    1. CF4
    2. PCl3
    3. SeF4
  4. Identify the electron pair geometry and the molecular structure of each of the following molecules:
    1. ClNO (N is the central atom)
    2. Cl2CO (C is the central atom)
    3. Cl2SO (S is the central atom)
    4. Cl2SeO (Se is the central atom)
    5. F2SO (S is the central atom)
  5. A molecule with the formula AB2, in which A and B represent different atoms, could have one of three different shapes. Sketch and name the three different shapes that this molecule might have. Give an example of a molecule or ion for each shape.
  6. A molecule with the formula AB3, in which A and B represent different atoms, could have one of three different shapes. Sketch and name the three different shapes that this molecule might have. Give an example of a molecule or ion that has each shape.
  7. Use the PhET Molecule Shape simulator to build a molecule. Starting with the central atom, click on the double bond to add one double bond. Then add one single bond and one lone pair. Rotate the molecule to observe the complete geometry. Name the electron group geometry and molecular structure and predict the bond angle. Then click the check boxes at the bottom and right of the simulator to check your answers.
  8. Use the PhET Molecule Shape simulator to explore real molecules. On the Real Molecules tab, select H2O. Switch between the “real” and “model” modes. Explain the difference observed.
  9. Use the PhET Molecule Shape simulator to explore real molecules. On the Real Molecules tab, select “model” mode and S2O. What is the model bond angle? Explain whether the “real” bond angle should be larger or smaller than the ideal model angle.

Glossary

bond angle: angle between any two covalent bonds that share a common atom

bond distance: (also, bond length) distance between the nuclei of two bonded atoms

electron-pair geometry: arrangement around a central atom of all regions of electron density (bonds, lone pairs, or unpaired electrons)

linear: shape in which two outside groups are placed on opposite sides of a central atom

molecular structure: structure that includes only the placement of the atoms in the molecule

tetrahedral: shape in which four outside groups are placed around a central atom such that a three-dimensional shape is generated with four corners and 109.5° angles between each pair and the central atom

trigonal planar: shape in which three outside groups are placed in a flat triangle around a central atom with 120° angles between each pair and the central atom

valence shell electron-pair repulsion theory (VSEPR): theory used to predict the bond angles in a molecule based on positioning regions of high electron density as far apart as possible to minimize electrostatic repulsion

vector: quantity having magnitude and direction