Uncertainty of Measurement

If you use a calculator to evaluate the expression 337 ÷ 217, you will get the following:

337 ÷ 217 = 1.55299539171…

and so on for many more digits.  Although this answer is correct, it is somewhat presumptuous. You start with two values that each have three digits, and the answer has twelve digits?  That does not make much sense from a strict numerical point of view.

Consider using a graduated cylinder to measure the volume of a liquid, as shown in Figure 2.1. The numbers of measured quantities, unlike defined or directly counted quantities, are not exact. To measure the volume of liquid in a graduated cylinder, you should make a reading at the bottom of the meniscus, the lowest point on the curved surface of the liquid.

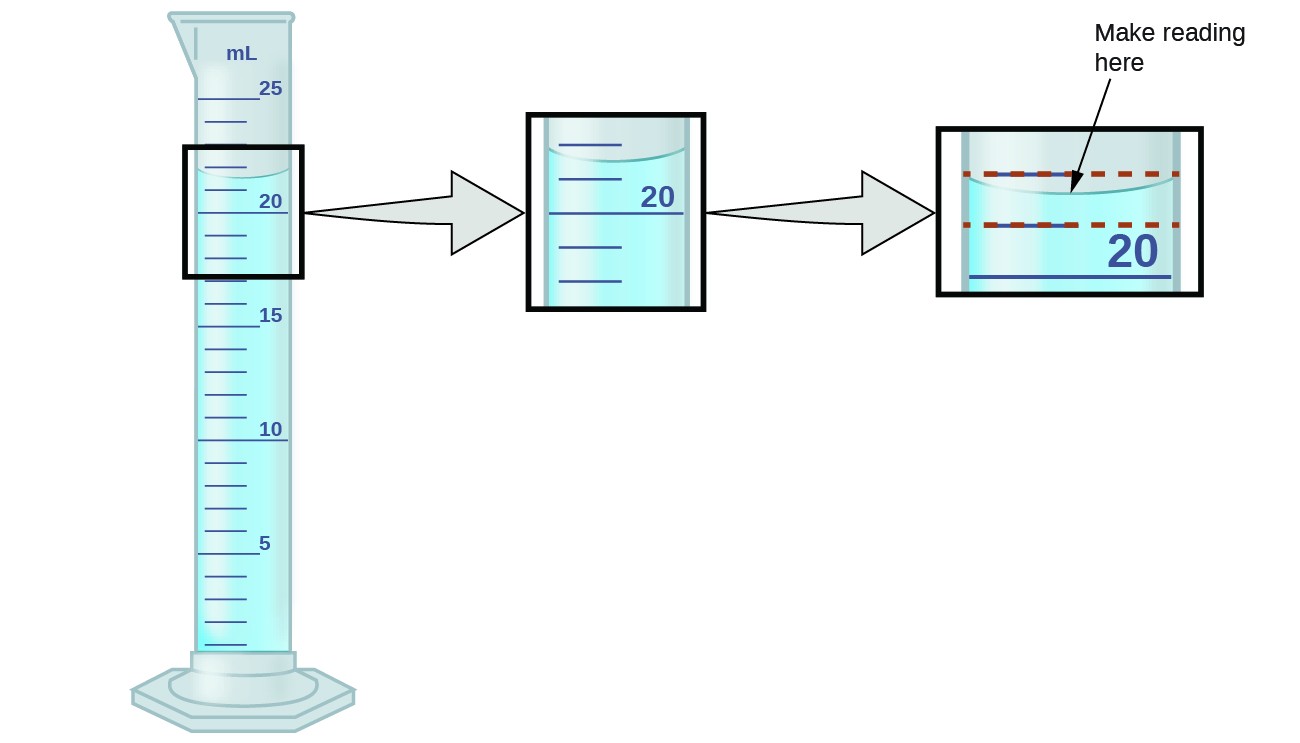
Figure 2.1. To measure the volume of liquid in this graduated cylinder, you must mentally subdivide the distance between the 21 and 22 mL marks into tenths of a milliliter, and then make a reading (estimate) at the bottom of the meniscus.

Refer to the illustration in Figure 2.1. The bottom of the meniscus in this case clearly lies between the 21 and 22 markings, meaning the liquid volume is certainly greater than 21 mL but less than 22 mL. The meniscus appears to be a bit closer to the 22-mL mark than to the 21-mL mark, and so a reasonable estimate of the liquid’s volume would be 21.6 mL. In the number 21.6, then, the digits 2 and 1 are certain, but the 6 is an estimate. Some people might estimate the meniscus position to be equally distant from each of the markings and estimate the tenth-place digit as 5, while others may think it to be even closer to the 22-mL mark and estimate this digit to be 7. Note that it would be pointless to attempt to estimate a digit for the hundredths place, given that the tenths-place digit is uncertain. In general, numerical scales such as the one on this graduated cylinder will permit measurements to one-tenth of the smallest scale division. The scale in this case has 1-mL divisions, and so volumes may be measured to the nearest 0.1 mL.

This concept holds true for all measurements, even if you do not actively make an estimate. If you place a quarter on a standard electronic balance, you may obtain a reading of 6.72 g. The digits 6 and 7 are certain, and the 2 indicates that the mass of the quarter is likely between 6.71 and 6.73 grams. The quarter weighs about 6.72 grams, with a nominal uncertainty in the measurement of ± 0.01 gram. If we weigh the quarter on a more sensitive balance, we may find that its mass is 6.723 g. This means its mass lies between 6.722 and 6.724 grams, an uncertainty of 0.001 gram. Every measurement has some uncertainty, which depends on the device used (and the user’s ability). All of the digits in a measurement, including the uncertain last digit, are called significant figures or significant digits. Note that zero may be a measured value; for example, if you stand on a scale that shows weight to the nearest pound and it shows “120,” then the 1 (hundreds), 2 (tens) and 0 (ones) are all significant (measured) values.

Example 1: uncertainty of Measurements

1. Record the following measurement to the proper number of significant figures
2. Record the following measurement to the proper number of significant figures

Show Answer

1. The arrow is between 4.0 and 5.0, so the measurement is at least 4.0. The arrow is between the third and fourth small tick marks, so it’s at least 0.3. We will have to estimate the last place. It looks like about one-third of the way across the space, so let us estimate the hundredths place as 3. Combining the digits, we have a measurement of 4.33 psi (psi stands for “pounds per square inch” and is a unit of pressure, like air in a tire). We say that the measurement is reported to three significant figures.
2. The rectangle is at least 1.0 cm wide but certainly not 2.0 cm wide, so the first significant digit is 1. The rectangle’s width is past the second tick mark but not the third; if each tick mark represents 0.1, then the rectangle is at least 0.2 in the next significant digit. We have to estimate the next place because there are no markings to guide us. It appears to be about halfway between 0.2 and 0.3, so we will estimate the next place to be a 5. Thus, the measured width of the rectangle is 1.25 cm. Again, the measurement is reported to three significant figures.

Check Your Learning

What would be the reported width of this rectangle?

Show Answer

0.63 cm

How Many Significant Figures are in a Given Measurement?

In many cases, you will be given a measurement. How do we know what digits are significant?  For example, the reported population of the United States is 306,000,000.  Does that mean that it is exactly three hundred six million or is some estimation occurring? Nonzero digits are always significant figures.  However, a zero may or not be significant.

The following conventions dictate which numbers in a reported measurement are significant and which are not significant:

So, by these rules, the population figure of the United States has only three significant figures: the 3, the 6, and the zero between them.  The remaining six zeros simply put the 306 in the millions position.