Objectives
After completing this section, you should be able to
- depict the staggered and eclipsed conformers of propane (or a similar compound) using sawhorse representations and Newman projections.
- sketch a graph of energy versus bond rotation for propane (or a similar compound) and discuss the graph in terms of torsional strain.
- depict the anti, gauche, eclipsed and fully eclipsed conformers of butane (or a similar compound), using sawhorse representations and Newman projections.
- sketch a graph of energy versus ($\ce{\sf{C{2}-C{3}}}$) bond rotation for butane (or a similar compound), and discuss it in terms of torsional and steric repulsion.
- assess which of two (or more) conformers of a given compound is likely to predominate at room temperature from a semi-quantitative knowledge of the energy costs of the interactions involved.
Key Terms
Make certain that you can define, and use in context, the key terms below.
- anti conformation
- gauche conformation
- eclipsed conformation
- steric repulsion
In butane, there are now three rotating carbon-carbon bonds to consider, but we will focus on the middle bond between C2 and C3. Below are two representations of butane in a conformation which puts the two CH3 groups (C1 and C4) in the eclipsed position.

This is the highest energy conformation for butane, due to what is called ‘van der Waals repulsion’, or ‘steric repulsion’, between the two rather bulky methyl groups.
What is van der Waals repulsion? Didn’t we just learn in Chapter 2 that the van der Waals force between two nonpolar groups is an attractive force? Consider this: you probably like to be near your friends, but no matter how close you are you probably don’t want to share a one-room apartment with five of them. When the two methyl groups are brought too close together, the overall resulting noncovalent interaction is repulsive rather than attractive. The result is that their respective electron densities repel one another.
If we rotate the front, (blue) carbon by 60°clockwise, the butane molecule is now in a staggered conformation.

This is more specifically referred to as the ‘gauche’ conformation of butane. Notice that although they are staggered, the two methyl groups are not as far apart as they could possibly be. There is still significant steric repulsion between the two bulky groups. A further rotation of 60°gives us a second eclipsed conformation (B) in which both methyl groups are lined up with hydrogen atoms.

Due to steric repulsion between methyl and hydrogen substituents, this eclipsed conformation B is higher in energy than the gauche conformation. However, because there is no methyl-to-methyl eclipsing, it is lower in energy than eclipsed conformation A.
One more 60 rotation produces the ‘anti’ conformation, where the two methyl groups are positioned opposite each other and steric repulsion is minimized.

This is the lowest energy conformation for butane.
The diagram below summarizes the relative energies for the various eclipsed, staggered, and gauche conformations.

At room temperature, butane is most likely to be in the lowest-energy anti conformation at any given moment in time, although the energy barrier between the anti and eclipsed conformations is not high enough to prevent constant rotation except at very low temperatures. For this reason (and also simply for ease of drawing), it is conventional to draw straight-chain alkanes in a zigzag form, which implies anti conformation at all carbon-carbon bonds.

The following diagram illustrates the change in potential energy that occurs with rotation about the C2–C3 bond.
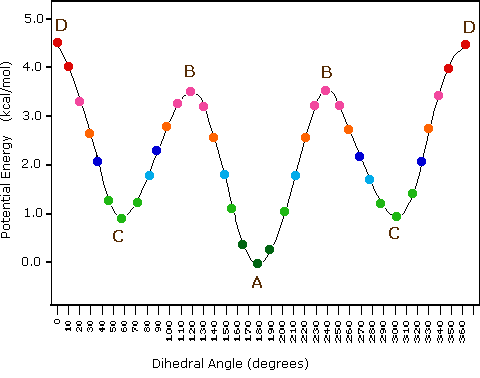
Figure X: Potential curve vs dihedral angle of the C2-C3 bond of butane.
Exercises
Exercises
Question
Draw the energy diagram for the rotation of the bond highlighted in pentane.
![]()
Solution
Contributors
- Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
- Prof. Steven Farmer (Sonoma State University)
- Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)
- Jim Clark (Chemguide.co.uk)
- William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry




