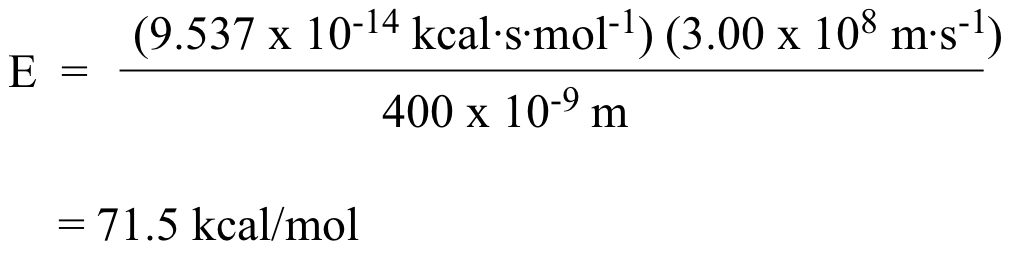The electromagnetic spectrum

Electromagnetic radiation, as you may recall from a previous chemistry or physics class, is composed of electrical and magnetic waves which oscillate on perpendicular planes. Visible light is electromagnetic radiation. So are the gamma rays that are emitted by spent nuclear fuel, the x-rays that a doctor uses to visualize your bones, the ultraviolet light that causes a painful sunburn when you forget to apply sun block, the infrared light that the army uses in night-vision goggles, the microwaves that you use to heat up your frozen burritos, and the radio-frequency waves that bring music to anybody who is old-fashioned enough to still listen to FM or AM radio.

Just like ocean waves, electromagnetic waves travel in a defined direction. While the speed of ocean waves can vary, however, the speed of electromagnetic waves – commonly referred to as the speed of light – is essentially a constant, approximately 300 million meters per second. This is true whether we are talking about gamma radiation or visible light. Obviously, there is a big difference between these two types of waves – we are surrounded by the latter for more than half of our time on earth, whereas we hopefully never become exposed to the former to any significant degree.  The different properties of the various types of electromagnetic radiation are due to differences in their wavelengths, and the corresponding differences in their energies: shorter wavelengths correspond to higher energy. 

High-energy radiation (such as gamma- and x-rays) is composed of very short waves – as short as 10^-16 meter from crest to crest.  Longer waves are far less energetic, and thus are less dangerous to living things.  Visible light waves are in the range of 400 – 700 nm (nanometers, or 10^-9 m), while radio waves can be several hundred meters in length.

The notion that electromagnetic radiation contains a quantifiable amount of energy can perhaps be better understood if we talk about light as a stream of particles, called photons, rather than as a wave. (Recall the concept known as ‘wave-particle duality’:  at the quantum level, wave behavior and particle behavior become indistinguishable, and very small particles have an observable ‘wavelength’). If we describe light as a stream of photons, the energy of a particular wavelength can be expressed as:

E =  hc/λ

where E is energy in kcal/mol,  λ (the Greek letter lambda) is wavelength in meters, c is 3.00 x 10⁸ m/s (the speed of light), and h is 9.537 x 10^-14 kcal•s•mol^-1, a number known as Planck’s constant.

Because electromagnetic radiation travels at a constant speed, each wavelength corresponds to a given frequency, which is the number of times per second that a crest passes a given point. Longer waves have lower frequencies, and shorter waves have higher frequencies.  Frequency is commonly reported in hertz (Hz),  meaning ‘cycles per second’, or ‘waves per second’. The standard unit for frequency is s^-1.

When talking about electromagnetic waves, we can refer either to wavelength or to frequency – the two values are interconverted using the simple expression:

λν = c

where ν (the Greek letter ‘nu’) is frequency in s^-1.  Visible red light with a wavelength of 700 nm, for example, has a frequency of 4.29 x 10¹⁴ Hz, and an energy of 40.9 kcal per mole of photons.

The full range of electromagnetic radiation wavelengths is referred to as the electromagnetic spectrum.

Notice in the figure above that visible light takes up just a narrow band of the full spectrum.  White light from the sun or a light bulb is a mixture of all of the visible wavelengths.  You see the visible region of the electromagnetic spectrum divided into its different wavelengths every time you see a rainbow: violet light has the shortest wavelength, and red light has the longest.

The energy of molecular vibration is quantized rather than continuous, meaning that a molecule can only stretch and bend at certain ‘allowed’ frequencies.  If a molecule is exposed to electromagnetic radiation that matches the frequency of one of its vibrational modes,  it will in most cases absorb energy from the radiation and jump to a higher vibrational energy state – what this means is that the amplitude of the vibration will increase, but the vibrational frequency will remain the same.  The difference in energy between the two vibrational states is equal to the energy associated with the wavelength of radiation that was absorbed.  It turns out that it is the infrared region of the electromagnetic spectrum which contains frequencies corresponding to the vibrational frequencies of organic bonds.

Let’s take 2-hexanone as an example.  Picture the carbonyl bond of the ketone group as a spring.  This spring is constantly bouncing back and forth, stretching and compressing, pushing the carbon and oxygen atoms further apart and then pulling them together.  This is the stretching mode of the carbonyl bond.  In the space of one second, the spring ‘bounces’ back and forth 5.15 x 10¹³ times – in other words,  the ground-state frequency of carbonyl  stretching for a the ketone group is about 5.15 x 10¹³ Hz.

If our ketone sample is irradiated with infrared light, the carbonyl bond will specifically absorb light with this same frequency, which by equations 4.1 and 4.2 corresponds to a wavelength of 5.83 x 10^-6 m and an energy of 4.91 kcal/mol.  When the carbonyl bond absorbs this energy, it jumps up to an excited vibrational state.

The value of ΔE – the energy difference between the low energy (ground)  and high energy (excited) vibrational states – is equal to 4.91 kcal/mol, the same as the energy associated with the absorbed light frequency.  The molecule does not remain in its excited vibrational state for very long, but quickly releases energy to the surrounding environment in form of heat, and returns to the ground state.

With an instrument called an infrared spectrophotometer, we can ‘see’ this vibrational transition.  In the spectrophotometer, infrared light with frequencies ranging from about 10¹³ to 10¹⁴ Hz  is passed though our sample of cyclohexane.  Most frequencies pass right through the sample and are recorded by a detector on the other side.

Our 5.15 x 10¹³ Hz carbonyl stretching frequency, however, is absorbed by the 2-hexanone sample, and so the detector records that the intensity of this frequency, after having passed through the sample, is something less than 100% of its initial intensity.

The vibrations of a 2-hexanone molecule are not, of course, limited to the simple stretching of the carbonyl bond.  The various carbon-carbon bonds also stretch and bend, as do the carbon-hydrogen bonds, and all of these vibrational modes also absorb different frequencies of infrared light.

The power of infrared spectroscopy arises from the observation that different functional groups have different characteristic absorption frequencies.   The carbonyl bond in a ketone, as we saw with our 2-hexanone example, typically absorbs in the range of  5.11 –  5.18 x 10¹³ Hz, depending on the molecule.   The carbon-carbon triple bond of an alkyne, on the other hand, absorbs in the range  6.30 – 6.80 x 10¹³ Hz.   The technique is therefore very useful as a means of identifying which functional groups are present in a molecule of interest.  If we pass infrared light through an unknown sample and find that it absorbs in the carbonyl frequency range but not in the alkyne range, we can infer that the molecule contains a carbonyl group but not an alkyne.

Some bonds absorb infrared light more strongly than others, and some bonds do not absorb at all. In order for a vibrational mode to absorb infrared light, it must result in a periodic change in the dipole moment of the molecule.  Such vibrations are said to be infrared active. In general, the greater the polarity of the bond, the stronger its IR absorption.  The carbonyl bond is very polar, and absorbs very strongly.  The carbon-carbon triple bond in most alkynes, in contrast, is much less polar, and thus a stretching vibration does not result in a large change in the overall dipole moment of the molecule. Alkyne groups absorb rather weakly compared to carbonyls.

Some kinds of vibrations are infrared inactive.  The stretching vibrations of completely symmetrical double and triple bonds, for example, do not result in a change in dipole moment, and therefore do not result in any absorption of light (but other bonds and vibrational modes in these molecules do absorb IR light).

Now, let’s  look at some actual output from IR spectroscopy experiments.  Below is the IR spectrum for 2-hexanone.

There are a number of things that need to be explained in order for you to understand what it is that we are looking at.  On the horizontal axis we see IR wavelengths expressed in terms of a unit called wavenumber (cm^-1), which tells us how many waves fit into one centimeter.   On the vertical axis we see ‘% transmittance’, which tells us how strongly light was absorbed at each frequency (100% transmittance means no absorption occurred at that frequency).  The solid line traces the values of % transmittance for every wavelength – the ‘peaks’ (which are actually pointing down) show regions of strong absorption.  For some reason, it is typical in IR spectroscopy to report wavenumber values rather than wavelength (in meters) or frequency (in Hz).  The ‘upside down’ vertical axis, with absorbance peaks pointing down rather than up, is also a curious convention in IR spectroscopy.  We wouldn’t  want to make things too easy for you!

Contributors

• Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
• Prof. Steven Farmer (Sonoma State University)
• William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
• Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)