8.4 Gas Laws

Boyle’s Law

The first relationship, discovered in the 17th century, is between the pressure of a gas and its volume. If the amount of gas in a sample and its temperature are kept constant, then as the pressure of a gas is increased, the volume of the gas decreases proportionately. This is an inverse relationship, written mathematically as

[latex]\text{P}\alpha\frac{1}{\text{V}}[/latex]

where the “∝” symbol means “is proportional to.” This is one form of Boyle’s law, which relates the pressure of a gas to its volume.  Figure 8.6 is a graph of Boyle’s data showing the downward curve typical of an inverse relationship.

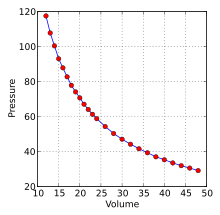
Figure 8.6 Graph of Boyle’s data on pressure and volume of a gas.  By Krishnavedala – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=16241859

A more useful form of Boyle’s law involves a change in conditions of a gas. For a given amount of gas at a constant temperature, if we know the initial pressure and volume of a gas sample and the pressure or volume changes, we can calculate what the new volume or pressure will be. That form of Boyle’s law is written

PiVi = PfVf

where the subscript i refers to initial conditions and the subscript f refers to final conditions.

To use PiVi = PfVf, you need to know any three of the variables so that you can algebraically calculate the fourth variable. Also, the pressure quantities must have the same units, as must the two volume quantities. If the two similar variables don’t have the same variables, one value must be converted to the other value’s unit.

Example 4

What happens to the volume of a gas if its pressure is increased? Assume all other conditions remain the same.

Solution

If the pressure of a gas is increased, the volume decreases in an inverse proportion.

Skill-Building Exercise

  1. What happens to the pressure of a gas if its volume is increased? Assume all other conditions remain the same.

Example 5

If a sample of gas has an initial pressure of 1.56 atm and an initial volume of 7.02 L, what is the final volume if the pressure is reduced to 0.987 atm? Assume that the amount and the temperature of the gas remain constant.

Solution

Identify the variables from the equation that are given in the problem.  1.56 atm is Pi, 7.02 L is Vi, and 0.987 atm is Pf. The unknown is the final volume—Vf. Use algebra to solve for Vf, then plug in the known numbers and calculate.

PiVi = PfVf

Dividing both sides by Pf  gives  [latex]\frac{\text{P}_\text{i}\text{V}_\text{i}}{\text{P}_\text{f}}=\frac{\cancel{\text{P}_\text{f}}\text{V}_\text{f}}{\cancel{\text{P}_\text{f}}}[/latex]

Turning the equation around and filling in values: [latex]\text{V}_\text{f}=\frac{1.56\cancel{\text{ atm}}\times{7.02\text{ L}}}{0.987\cancel{\text{ atm}}}=11.1\text{ L}[/latex]

Check whether the answer makes sense.  Pressure and volume are inversely related, so when pressure decreases, volume should increase, and the calculated answer makes sense.

Skill-Building Exercise

  1. If a sample of gas has an initial pressure of 3.66 atm and an initial volume of 11.8 L, what is the final pressure if the volume is reduced to 5.09 L? Assume that the amount and the temperature of the gas remain constant.

If the units of similar quantities are not the same, one of them must be converted to the other quantity’s units for the calculation to work out properly. It does not matter which quantity is converted to a different unit; the only thing that matters is that the conversion and subsequent algebra are performed properly. The following example illustrates this process.

Example 6

If a sample of gas has an initial pressure of 1.56 atm and an initial volume of 7.02 L, what is the final volume if the pressure is changed to 1,775 torr? Does the answer make sense? Assume that the amount and the temperature of the gas remain constant.

Solution

This example is similar to Example 5, with two exceptions: the unknown is Vf and the two pressures are expressed in different units. The units cancel only if the two pressures are expressed in the same unit, and it does not matter which one is changed. We will arbitrarily change the initial pressure from atm to torr:

[latex]1.56\cancel{\text{ atm}}\times{\frac{760\text{ torr}}{1\cancel{\text{ atm}}}}=1190\text{ torr}[/latex]

Now we can use Boyle’s law:  PiVi = PfVf but must rearrange to solve for Vf by dividing both sides by Pf before plugging in numbers.

[latex]\text{V}_\text{f}=\frac{\text{P}_\text{i}\text{V}_\text{i}}{\text{P}_\text{f}}[/latex]            so       [latex]\text{V}_\text{f}=\frac{1190\cancel{\text{ torr}}\times7.02\text{ L}}{1775\cancel{\text{ torr}}}=4.71\text{ L}[/latex]

Because the pressure increases, it makes sense that the volume decreases.

Skill-Building Exercise

  1. If a sample of gas has an initial pressure of 375 torr and an initial volume of 7.02 L, what is the final pressure if the volume is changed to 4,577 mL? Does the answer make sense? Assume that amount and the temperature of the gas remain constant.

To Your Health: Breathing

Breathing certainly is a major contribution to your health! Without breathing, we could not survive. Curiously, the act of breathing itself is little more than an application of Boyle’s law.

The lungs are a series of ever-narrowing tubes that end in a myriad of tiny sacs called alveoli. It is in the alveoli that oxygen from the air transfers to the bloodstream and carbon dioxide from the bloodstream transfers to the lungs for exhalation. For air to move in and out of the lungs, the volume inside the lungs must change, forcing the lungs to change pressure, just as predicted by Boyle’s law.  The difference between the pressure in the lungs and atmospheric pressure causes air to move from the region with greater pressure to the region with lower pressure.

The volume change is caused by the diaphragm, a sheet of muscle at the base of the lungs. During inhalation, the diaphragm contracts, flattens out, and moves down, expanding the volume of the lungs. Based on Boyle’s law, the increased volume is accompanied by a decrease in air pressure inside the lungs. Outside air pressure is greater, so air moves into the lungs. The pressure decrease is slight—only 3 torr, or about 0.4% of an atmosphere. We inhale only 0.5–1.0 L of air per normal breath.

During exhalation,  the diaphragm relaxes, moving upward into a domed shape. This slightly decreases the volume of the lungs, which according to Boyle’s law, slightly increases the pressure of the air in the lungs.  With the pressure of air in the lungs  about 1-2 torr higher than the outside air pressure, air leaves the lungs.  So with every breath, our own bodies rely on Boyle’s law.

Charles’s Law

Another simple gas law relates the volume of a gas to its temperature. Experiments indicate that as the temperature of a gas sample is increased, its volume increases as long as the pressure and the amount of gas remain constant. The way to write this mathematically is

V ∝ T

At this point, the concept of temperature must be clarified. Although the Kelvin scale is the preferred temperature scale, the Celsius scale is also a common temperature scale used in science. The Celsius scale is based on the melting and boiling points of water and is actually the common temperature scale used by most countries around the world. The only holdouts which still use the Fahrenheit scale are the Bahamas, Belize, the Cayman Islands, Palau, and the United States and its territories. The value of a Celsius temperature is directly related to its Kelvin value by a simple expression:

Kelvin temperature = Celsius temperature + 273.15*

Thus, it is easy to convert from one temperature scale to another.

*If the Celsius temperature is measured to the ones place, use 273.  If the measurement has the tenths place, use 273.2.  If hundredths are given, use 273.15.

Note

The Kelvin scale is an absolute scale because the zero point on the Kelvin scale is the coldest possible temperature, the temperature at which there is no movement of atoms and molecules. On the other temperature scales, absolute zero is −273.2°C, −459.7°F.  In Kelvin, if the temperature doubles, molecules actually have twice as much thermal energy.  That is not true in the relative scales Fahrenheit and Celsius.  For example, air molecules do not have much more thermal energy on a 90oF day than they have on a 45oF day, not even close to twice as much.

The expression relating a gas volume to its temperature begs the following question: to which temperature scale is the volume of a gas related? The answer is that gas volumes are directly related to the Kelvin temperature. Therefore, the temperature of a gas sample should always be expressed in (or converted to) a Kelvin temperature.

Example 7

What happens to the volume of a gas if its temperature is decreased? Assume that all other conditions remain constant.

Solution

If the temperature of a gas sample is decreased, the volume decreases as well.

Skill-Building Exercise

  1. What happens to the temperature of a gas if its volume is increased? Assume that all other conditions remain constant.

 

As with Boyle’s law, the relationship between volume and temperature can be expressed in terms of initial and final values of volume and temperature, as follows:

[latex]\frac{\text{V}_\text{i}}{\text{T}_\text{i}}=\frac{\text{V}_\text{f}}{\text{T}_\text{f}}[/latex]

where Vi and Ti are the initial volume and temperature, and Vf and Tf are the final volume and temperature. This is Charles’s law. The restriction on its use is that the pressure of the gas and the amount of gas must remain constant.

Example 8

A gas sample at 20.°C has an initial volume of 20.0 L. What is its volume if the temperature is changed to 60.°C? Does the answer make sense? Assume that the pressure and the amount of the gas remain constant.

Solution

Although the temperatures are given in degrees Celsius, we must convert them to the kelvins before we can use Charles’s law. Thus,

20.°C + 273 = 293 K = Ti
60.°C + 273 = 333 K = Tf

Next, solve the Charles’s Law equation for Vf , substitute in the known values, perform the calculation, and check whether the answer is reasonable.

[latex]\frac{\text{V}_\text{i}\text{T}_\text{f}}{\text{T}_\text{i}}=\frac{\text{V}_\text{f}\cancel{\text{T}_\text{f}}}{\cancel{\text{T}_\text{f}}}[/latex]    so   [latex]\text{V}_\text{f}=\frac{\text{V}_\text{i}\text{T}_\text{f}}{\text{T}_\text{i}}=\frac{333\cancel{\text{ K}}\times{20.0\text{ L}}}{293\cancel{\text{ K}}}=22.7\text{ L}[/latex]

This makes sense because volume increased as the temperature increased.

Skill-Building Exercise

  1. A gas sample at 35°C has an initial volume of 5.06 L. What is its volume if the temperature is changed to −35°C? Does the answer make sense? Assume that the pressure and the amount of the gas remain constant.

 

Combined Gas Law

Other gas laws can be constructed, but we will focus on only two more. The combined gas law brings Boyle’s and Charles’s laws together to relate pressure, volume, and temperature changes of a gas sample:

[latex]\frac{\text{P}_\text{i}\text{V}_\text{i}}{\text{T}_\text{i}}=\frac{\text{P}_\text{f}\text{V}_\text{f}}{\text{T}_\text{f}}[/latex]

To apply this gas law, the amount of gas should remain constant. As with the other gas laws, the temperature must be expressed in kelvins, and the units on the similar quantities should be the same. Because of the dependence on three quantities at the same time, it is difficult to tell in advance what will happen to one property of a gas sample as two other properties change. The best way to know is to work it out mathematically.

Example 9

A sample of gas has Pi = 1.50 atm, Vi = 10.5 L, and Ti = 300 K. What is the final volume if Pf = 0.750 atm and Tf = 350 K?

Solution: Use algebra to isolate Vf , then plug in values and calculate.

[latex]\frac{\text{P}_\text{i}\text{V}_\text{i}\text{T}_\text{f}}{\text{T}_\text{i}\text{P}_\text{f}}=\frac{\cancel{\text{P}_\text{f}}\text{V}_\text{f}\cancel{\text{T}_\text{f}}}{\cancel{\text{T}_\text{f}}\cancel{\text{P}_\text{f}}}[/latex]      so    [latex]\text{V}_\text{f}=\frac{\text{P}_\text{i}\text{V}_\text{i}\text{T}_\text{f}}{\text{T}_\text{i}\text{P}_\text{f}}=\frac{1.50\cancel{\text{ atm}}\times{10.5\text{ L}}\times{350\cancel{\text{ K}}}}{{\left(300\cancel{\text{ K}}\times{0.750\cancel{\text{ atm}}}\right)}}=24.5\text{ L}[/latex]

Skill-Building Exercise

  1. A sample of gas has Pi = 0.768 atm, Vi = 10.5 L, and Ti = 300 K. What is the final pressure if Vf = 7.85 L and Tf = 250 K?

Example 10

A balloon containing a sample of gas has a temperature of 22°C and a pressure of 1.09 atm in an airport in Cleveland. The balloon has a volume of 1,070 mL. The balloon is transported by plane to Denver, where the temperature is 11°C and the pressure is 655 torr. What is the new volume of the balloon?

Solution: Notice that this problem is very similar to Example 9.  The only difference is that some of the given values are not expressed in the right units and must be converted to the right units before plugging them into the equation.

The temperatures must be expressed in kelvins, and the pressure units are different so one of the quantities must be converted. Let us convert the atm to torr:

22°C + 273 = 295 K = Ti
11°C + 273 = 284 K = Tf
1.09  atm×[latex]\frac{760\text{ torr}}{1\text{ atm}}[/latex]=828 torr = Pi

Using the rearranged version of the combined gas law from Example 9 and plugging in the values for Problem 10:

[latex]\text{V}_\text{f}=\frac{\text{P}_\text{i}\text{V}_\text{i}\text{T}_\text{f}}{\text{T}_\text{i}\text{P}_\text{f}}=\frac{828\cancel{\text{ torr}}\times{1070\text{ mL}}\times{284\cancel{\text{ K}}}}{{\left(295\cancel{\text{ K}}\times{655\cancel{\text{ torr}}}\right)}}=1300\text{ mL}[/latex]

This is better expressed as 1.30 x 103 mL since the answer should have 3 sig figs.

Skill-Building Exercise

  1. A balloon used to lift weather instruments into the atmosphere contains gas having a volume of 1,150 L on the ground, where the pressure is 0.977 atm and the temperature is 18°C. Aloft, this gas has a pressure of 6.88 torr and a temperature of −15°C. What is the new volume of the gas?

 

The Ideal Gas Law

So far, the gas laws we have used have focused on changing one or more properties of the gas, such as its volume, pressure, or temperature. There is one gas law that relates all the independent properties of a gas under any particular condition, rather than a change in conditions. This gas law is called the ideal gas law. The formula of this law is as follows:

PV = nRT

In this equation, P is pressure, V is volume, n is amount of moles, and T is Kelvin temperature. R is called the ideal gas law constant and is a proportionality constant that relates the values of pressure, volume, amount, and temperature of a gas sample. The variables in this equation do not have the subscripts i and f to indicate an initial condition and a final condition. The ideal gas law relates the four independent properties of a gas under any conditions.

The value of R depends on what units are used to express the other quantities. If volume is expressed in liters and pressure in atmospheres, then the proper value of R is as follows:

R=0.08205 [latex]\frac{\text{L atm}}{\text{mol K}}[/latex]

This may seem like a strange unit, but that is what is required for the units to cancel.

Example 11

What is the volume in liters of 1.45 mol of N2 gas at 298 K and 3.995 atm?

Solution:

Using the ideal gas law, solve for V, then plug in the known values.

[latex]\frac{\cancel{\text{P}}\text{V}}{\cancel{\text{P}}}=\frac{\text{nRT}}{\text{P}}[/latex]  so   [latex]V=\frac{1.45\cancel{\text{mol}}\times{0.08205\frac{\text{L}{\cancel{\text{ atm}}}}{\cancel{\text{mol}}\cancel{\text{ K}}}}\times{298\cancel{\text{ K}}}}{3.995\cancel{\text{ atm}}}=8.87\text{ L}[/latex]

Note that the conditions of the gas are not changing. Rather, the ideal gas law allows us to determine what the fourth property of a gas (here, volume) must be if three other properties (here, amount, pressure, and temperature) are known.

Skill-Building Exercise

  1. What is the pressure of a sample of CO2 gas if 0.557 mol is held in a 20.0 L container at 451 K?

For convenience, scientists have selected 273.15 K (0°C) and 1.00 atm pressure as a set of standard conditions for gases. This combination of conditions is called standard temperature and pressure (STP). Under these conditions, 1 mol of any gas has about the same volume, 22.4 L. Because this volume is independent of the identity of a gas, the idea that 1 mol of gas has a volume of 22.4 L at STP makes a convenient conversion factor:

1 mol gas = 22.4 L (at STP)

Example 12

Cyclopropane (C3H6) is a gas that formerly was used as an anesthetic. How many moles of gas are there in a 100.0 L sample if the gas is at STP?

Solution

We can set up a simple, one-step conversion that relates moles and liters:

[latex]100.0\text{ L C}_3\text{H}_6\times{\frac{1\text{ mol}}{22.4\text{ L}}}=4.46\text{ mol C}_3\text{H}_6[/latex]

Skill-Building Exercise

  1. Freon is a trade name for a series of fluorine- and chlorine-containing gases that formerly were used in refrigeration systems. What volume does 8.75 mol of Freon have at STP?

Note

Many gases known as Freon are no longer used because their presence in the atmosphere destroys the ozone layer, which protects us from ultraviolet light from the sun.

Career Focus: Respiratory Therapist

Certain diseases—such as emphysema, lung cancer, and severe asthma—primarily affect the lungs. Respiratory therapists help patients with breathing-related problems. They can evaluate, help diagnose, and treat breathing disorders and even help provide emergency assistance in acute illness where breathing is compromised.

Most respiratory therapists must complete at least two years of college and earn an associate’s degree, although therapists can assume more responsibility if they have a bachelor’s degree. Therapists must also pass state or national certification exams. Once certified, respiratory therapists can work in hospitals, doctor’s offices, nursing homes, or patient’s homes. Therapists work with equipment such as oxygen tanks and respirators, may sometimes dispense medication to aid in breathing, perform tests, and educate patients in breathing exercises and other therapy.

Because respiratory therapists work directly with patients, the ability to work well with others is a must for this career. It is an important job because it deals with one of the most crucial functions of the body.

Concept Review Exercises

  1. What properties do the gas laws help us predict?

  2. What makes the ideal gas law different from the other gas laws?

Answers

Key Takeaway

  • The physical properties of gases are predictable using mathematical formulas known as gas laws.

Exercises

  1. What conditions of a gas sample should remain constant for Boyle’s law to be used?

  2. What conditions of a gas sample should remain constant for Charles’s law to be used?

  3. Does the identity of a gas matter when using Boyle’s law? Why or why not?

  4. Does the identity of a gas matter when using Charles’s law? Why or why not?

  5. A sample of nitrogen gas is confined to a balloon that has a volume of 1.88 L and a pressure of 1.334 atm. What will be the volume of the balloon if the pressure is changed to 0.662 atm? Assume that the temperature and the amount of the gas remain constant.

  6. A sample of helium gas in a piston has a volume of 86.4 mL under a pressure of 447 torr. What will be the volume of the helium if the pressure on the piston is increased to 1,240 torr? Assume that the temperature and the amount of the gas remain constant.

  7. If a gas has an initial pressure of 24,650 Pa and an initial volume of 376 mL, what is the final volume if the pressure of the gas is changed to 775 torr? Assume that the amount and the temperature of the gas remain constant.

  8. A gas sample has an initial volume of 0.9550 L and an initial pressure of 564.5 torr. What would the final pressure of the gas be if the volume is changed to 587.0 mL? Assume that the amount and the temperature of the gas remain constant.

  9. A person draws a normal breath of about 1.00 L. If the initial temperature of the air is 18°C and the air warms to 37°C, what is the new volume of the air? Assume that the pressure and amount of the gas remain constant.

  10. A person draws a normal breath of about 1.00 L. If the initial temperature of the air is −10°C and the air warms to 37°C, what is the new volume of the air? Assume that the pressure and the amount of the gas remain constant.

  11. An air/gas vapor mix in an automobile cylinder has an initial temperature of 450 K and a volume of 12.7 cm3. The gas mix is heated to 565°C. If pressure and amount are held constant, what is the final volume of the gas in cubic centimeters?

  12. Given the following conditions for a gas: Vi = 0.665 L, Ti = 23.6°C, Vf = 1.034 L. What is Tf in degrees Celsius and kelvins?

  13. Assuming the amount remains the same, what must be the final volume of a gas that has an initial volume of 387 mL, an initial pressure of 456 torr, an initial temperature of 65.0°C, a final pressure of 1.00 atm, and a final temperature of 300 K?

  14. When the nozzle of a spray can is depressed, 0.15 mL of gas expands to 0.44 mL, and its pressure drops from 788 torr to 1.00 atm. If the initial temperature of the gas is 22.0°C, what is the final temperature of the gas?

  15. Use the ideal gas law to show that 1 mol of a gas at STP has a volume of about 22.4 L.

  16. Use a standard conversion factor to determine a value of the ideal gas law constant R that has units of L·torr/mol·K.

  17. How many moles of gas are there in a 27.6 L sample at 298 K and a pressure of 1.44 atm?

  18. How many moles of gas are there in a 0.066 L sample at 298 K and a pressure of 0.154 atm?

  19. A 0.334 mol sample of carbon dioxide gas is confined to a volume of 20.0 L and has a pressure of 0.555 atm. What is the temperature of the carbon dioxide in kelvins and degrees Celsius?

  20. What must V be for a gas sample if n = 4.55 mol, P = 7.32 atm, and T = 285 K?

  21. What is the pressure of 0.0456 mol of Ne gas contained in a 7.50 L volume at 29°C?

  22. What is the pressure of 1.00 mol of Ar gas that has a volume of 843.0 mL and a temperature of −86.0°C?

Answers