5.5 Substitution

Learning Objectives

  • Use substitution to evaluate indefinite integrals.
  • Use substitution to evaluate definite integrals.

The Fundamental Theorem of Calculus gave us a method to evaluate integrals without using Riemann sums. The drawback of this method, though, is that we must be able to find an antiderivative, and this is not always easy. In this section we examine a technique, called integration by substitution, to help us find antiderivatives. Specifically, this method helps us find antiderivatives when the integrand is the result of a chain-rule derivative.

At first, the approach to the substitution procedure may not appear very obvious. However, it is primarily a visual task—that is, the integrand shows you what to do; it is a matter of recognizing the form of the function. So, what are we supposed to see? We are looking for an integrand of the form [latex]f\left[g(x)\right]{g}^{\prime }(x)dx.[/latex] For example, in the integral [latex]\int {({x}^{2}-3)}^{3}2xdx,[/latex] we have [latex]f(x)={x}^{3},g(x)={x}^{2}-3,[/latex] and [latex]g\text{'}(x)=2x.[/latex] Then,

[latex]f\left[g(x)\right]{g}^{\prime }(x)={({x}^{2}-3)}^{3}(2x),[/latex]

and we see that our integrand is in the correct form.

The method is called substitution because we substitute part of the integrand with the variable [latex]u[/latex] and part of the integrand with du. It is also referred to as change of variables because we are changing variables to obtain an expression that is easier to work with for applying the integration rules.

Substitution with Indefinite Integrals

Let [latex]u=g(x),,[/latex] where [latex]{g}^{\prime }(x)[/latex] is continuous over an interval, let [latex]f(x)[/latex] be continuous over the corresponding range of [latex]g[/latex], and let [latex]F(x)[/latex] be an antiderivative of [latex]f(x).[/latex] Then,

[latex]\begin{array}{cc}\int f\left[g(x)\right]{g}^{\prime }(x)dx\hfill & =\int f(u)du\hfill \\ & =F(u)+C\hfill \\ & =F(g(x))+C.\hfill \end{array}[/latex]

Proof

Let [latex]f[/latex], [latex]g[/latex], [latex]u[/latex], and F be as specified in the theorem. Then

[latex]\begin{array}{cc}\frac{d}{dx}F(g(x))\hfill & ={F}^{\prime }(g(x)){g}^{\prime }(x)\hfill \\ & =f\left[g(x)\right]{g}^{\prime }(x).\hfill \end{array}[/latex]

Integrating both sides with respect to [latex]x[/latex], we see that

[latex]\int f\left[g(x)\right]{g}^{\prime }(x)dx=F(g(x))+C.[/latex]

If we now substitute [latex]u=g(x),[/latex] and [latex]du=g\text{'}(x)dx,[/latex] we get

[latex]\begin{array}{cc}\int f\left[g(x)\right]{g}^{\prime }(x)dx\hfill & =\int f(u)du\hfill \\ & =F(u)+C\hfill \\ & =F(g(x))+C.\hfill \end{array}[/latex]

□

Returning to the problem we looked at originally, we let [latex]u={x}^{2}-3[/latex] and then [latex]du=2xdx.[/latex] Rewrite the integral in terms of [latex]u[/latex]:

[latex]{\int \underset{u}{\underbrace{({x}^{2}-3)}}}^{3}\underset{du}{\underbrace{(2xdx)}}=\int {u}^{3}du.[/latex]

Using the power rule for integrals, we have

[latex]\int {u}^{3}du=\frac{{u}^{4}}{4}+C.[/latex]

Substitute the original expression for [latex]x[/latex] back into the solution:

[latex]\frac{{u}^{4}}{4}+C=\frac{{({x}^{2}-3)}^{4}}{4}+C.[/latex]

We can generalize the procedure in the following Problem-Solving Strategy.

Problem-Solving Strategy: Integration by Substitution

  1. Look carefully at the integrand and select an expression [latex]g(x)[/latex] within the integrand to set equal to [latex]u[/latex]. Let’s select [latex]g(x).[/latex] such that [latex]{g}^{\prime }(x)[/latex] is also part of the integrand.
  2. Substitute [latex]u=g(x)[/latex] and [latex]du={g}^{\prime }(x)dx.[/latex] into the integral.
  3. We should now be able to evaluate the integral with respect to [latex]u[/latex]. If the integral can’t be evaluated we need to go back and select a different expression to use as [latex]u[/latex].
  4. Evaluate the integral in terms of [latex]u[/latex].
  5. Write the result in terms of [latex]x[/latex] and the expression [latex]g(x).[/latex]

Using Substitution to Find an Antiderivative

Use substitution to find the antiderivative of [latex]\int 6x{(3{x}^{2}+4)}^{4}dx.[/latex]

Use substitution to find the antiderivative of [latex]\int 3{x}^{2}{({x}^{3}-3)}^{2}dx.[/latex]

[latex]\int 3{x}^{2}{({x}^{3}-3)}^{2}dx=\frac{1}{3}{({x}^{3}-3)}^{3}+C[/latex]

Hint

Let [latex]u={x}^{3}-3.[/latex]

Sometimes we need to adjust the constants in our integral if they don’t match up exactly with the expressions we are substituting.

Using Substitution with Alteration

Use substitution to find the antiderivative of [latex]\int z\sqrt{{z}^{2}-5}dz.[/latex]

Use substitution to find the antiderivative of [latex]\int {x}^{2}{({x}^{3}+5)}^{9}dx.[/latex]

Hint

Multiply the du equation by [latex]\frac{1}{3}.[/latex]

Using Substitution with Integrals of Trigonometric Functions

Use substitution to evaluate the integral [latex]\int \frac{ \sin t}{{ \cos }^{3}t}dt.[/latex]

Use substitution to evaluate the integral [latex]\int \frac{ \cos t}{{ \sin }^{2}t}dt.[/latex]

Hint

Use the process from (Figure) to solve the problem.

Sometimes we need to manipulate an integral in ways that are more complicated than just multiplying or dividing by a constant. We need to eliminate all the expressions within the integrand that are in terms of the original variable. When we are done, [latex]u[/latex] should be the only variable in the integrand. In some cases, this means solving for the original variable in terms of [latex]u[/latex]. This technique should become clear in the next example.

Finding an Antiderivative Using [latex]u[/latex]-Substitution

Use substitution to find the antiderivative of [latex]\int \frac{x}{\sqrt{x-1}}dx.[/latex]

Use substitution to evaluate the indefinite integral [latex]\int { \cos }^{3}t \sin tdt.[/latex]

Hint

Use the process from (Figure) to solve the problem.

Substitution for Definite Integrals

Substitution can be used with definite integrals, too. However, using substitution to evaluate a definite integral requires a change to the limits of integration. If we change variables in the integrand, the limits of integration change as well.

Substitution with Definite Integrals

Let [latex]u=g(x)[/latex] and let [latex]{g}^{\text{′}}[/latex] be continuous over an interval [latex]\left[a,b\right],[/latex] and let [latex]f[/latex] be continuous over the range of [latex]u=g(x).[/latex] Then,

[latex]{\int }_{a}^{b}f(g(x)){g}^{\prime }(x)dx={\int }_{g(a)}^{g(b)}f(u)du.[/latex]

Although we will not formally prove this theorem, we justify it with some calculations here. From the substitution rule for indefinite integrals, if [latex]F(x)[/latex] is an antiderivative of [latex]f(x),[/latex] we have

[latex]\int f(g(x)){g}^{\prime }(x)dx=F(g(x))+C.[/latex]

Then

[latex]\begin{array}{cc}{\int }_{a}^{b}f\left[g(x)\right]{g}^{\prime }(x)dx\hfill & ={F(g(x))|}_{x=a}^{x=b}\hfill \\ & =F(g(b))-F(g(a))\hfill \\ & ={F(u)|}_{u=g(a)}^{u=g(b)}\hfill \\ \\ \\ & ={\int }_{g(a)}^{g(b)}f(u)du,\hfill \end{array}[/latex]

and we have the desired result.

Using Substitution to Evaluate a Definite Integral

Use substitution to evaluate [latex]{\int }_{0}^{1}{x}^{2}{(1+2{x}^{3})}^{5}dx.[/latex]

Use substitution to evaluate the definite integral [latex]{\int }_{-1}^{0}y{(2{y}^{2}-3)}^{5}dy.[/latex]

Hint

Use the steps from (Figure) to solve the problem.

Using Substitution with an Exponential Function

Use substitution to evaluate [latex]{\int }_{0}^{1}x{e}^{4{x}^{2}+3}dx.[/latex]

Use substitution to evaluate [latex]{\int }_{0}^{1}{x}^{2} \cos (\frac{\pi }{2}{x}^{3})dx.[/latex]

Hint

Use the process from (Figure) to solve the problem.

Substitution may be only one of the techniques needed to evaluate a definite integral. All of the properties and rules of integration apply independently, and trigonometric functions may need to be rewritten using a trigonometric identity before we can apply substitution. Also, we have the option of replacing the original expression for [latex]u[/latex] after we find the antiderivative, which means that we do not have to change the limits of integration. These two approaches are shown in (Figure).

Using Substitution to Evaluate a Trigonometric Integral

Use substitution to evaluate [latex]{\int }_{0}^{\pi \text{/}2}{ \cos }^{2}\theta d\theta .[/latex]

Key Concepts

  • Substitution is a technique that simplifies the integration of functions that are the result of a chain-rule derivative. The term ‘substitution’ refers to changing variables or substituting the variable [latex]u[/latex] and du for appropriate expressions in the integrand.
  • When using substitution for a definite integral, we also have to change the limits of integration.

Key Equations

  • Substitution with Indefinite Integrals
    [latex]\int f\left[g(x)\right]{g}^{\prime }(x)dx=\int f(u)du=F(u)+C=F(g(x))+C[/latex]
  • Substitution with Definite Integrals
    [latex]{\int }_{a}^{b}f(g(x))g\text{'}(x)dx={\int }_{g(a)}^{g(b)}f(u)du[/latex]

1. Why is [latex]u[/latex]-substitution referred to as change of variable?

2. If [latex]f=g\circ h,[/latex] when reversing the chain rule, [latex]\frac{d}{dx}(g\circ h)(x)={g}^{\prime }(h(x)){h}^{\prime }(x),[/latex] should you take [latex]u=g(x)[/latex] or [latex]u=h(x)?[/latex]

In the following exercises, verify each identity using differentiation. Then, using the indicated [latex]u[/latex]-substitution, identify [latex]f[/latex] such that the integral takes the form [latex]\int f(u)du.[/latex]

3. [latex]\int x\sqrt{x+1}dx=\frac{2}{15}{(x+1)}^{3\text{/}2}(3x-2)+C;u=x+1[/latex]

4. [latex]\int \frac{{x}^{2}}{\sqrt{x-1}}dx(x>1)=\frac{2}{15}\sqrt{x-1}(3{x}^{2}+4x+8)+C;u=x-1[/latex]

5. [latex]\int x\sqrt{4{x}^{2}+9}dx=\frac{1}{12}{(4{x}^{2}+9)}^{3\text{/}2}+C;u=4{x}^{2}+9[/latex]

6. [latex]\int \frac{x}{\sqrt{4{x}^{2}+9}}dx=\frac{1}{4}\sqrt{4{x}^{2}+9}+C;u=4{x}^{2}+9[/latex]

7. [latex]\int \frac{x}{{(4{x}^{2}+9)}^{2}}dx=-\frac{1}{8(4{x}^{2}+9)};u=4{x}^{2}+9[/latex]

In the following exercises, find the antiderivative using the indicated substitution.

8. [latex]\int {(x+1)}^{4}dx;u=x+1[/latex]

9. [latex]\int {(x-1)}^{5}dx;u=x-1[/latex]

10. [latex]\int {(2x-3)}^{-7}dx;u=2x-3[/latex]

11. [latex]\int {(3x-2)}^{-11}dx;u=3x-2[/latex]

12. [latex]\int \frac{x}{\sqrt{{x}^{2}+1}}dx;u={x}^{2}+1[/latex]

13. [latex]\int \frac{x}{\sqrt{1-{x}^{2}}}dx;u=1-{x}^{2}[/latex]

14. [latex]\int (x-1){({x}^{2}-2x)}^{3}dx;u={x}^{2}-2x[/latex]

15. [latex]\int ({x}^{2}-2x){({x}^{3}-3{x}^{2})}^{2}dx;u={x}^{3}=3{x}^{2}[/latex]

16. [latex]\int { \cos }^{3}\theta d\theta ;u= \sin \theta[/latex]([latex]Hint\text{:}{ \cos }^{2}\theta =1-{ \sin }^{2}\theta[/latex])

17. [latex]\int { \sin }^{3}\theta d\theta ;u= \cos \theta[/latex][latex](Hint\text{:}{ \sin }^{2}\theta =1-{ \cos }^{2}\theta)[/latex]

In the following exercises, use a suitable change of variables to determine the indefinite integral.

18. [latex]\int x{(1-x)}^{99}dx[/latex]

19. [latex]\int t{(1-{t}^{2})}^{10}dt[/latex]

20. [latex]\int {(11x-7)}^{-3}dx[/latex]

21. [latex]\int {(7x-11)}^{4}dx[/latex]

22. [latex]\int { \cos }^{3}\theta \sin \theta d\theta[/latex]

23. [latex]\int { \sin }^{7}\theta \cos \theta d\theta[/latex]

24. [latex]\int { \cos }^{2}(\pi t) \sin (\pi t)dt[/latex]

25. [latex]\int { \sin }^{2}x{ \cos }^{3}xdx[/latex][latex](Hint\text{:}{ \sin }^{2}x+{ \cos }^{2}x=1)[/latex]

26. [latex]\int t \sin ({t}^{2}) \cos ({t}^{2})dt[/latex]

27. [latex]\int {t}^{2}{ \cos }^{2}({t}^{3}) \sin ({t}^{3})dt[/latex]

28. [latex]\int \frac{{x}^{2}}{{({x}^{3}-3)}^{2}}dx[/latex]

29. [latex]\int \frac{{x}^{3}}{\sqrt{1-{x}^{2}}}dx[/latex]

30. [latex]\int \frac{{y}^{5}}{{(1-{y}^{3})}^{3\text{/}2}}dy[/latex]

31. [latex]{\int \cos \theta (1- \cos \theta )}^{99} \sin \theta d\theta[/latex]

32. [latex]{\int (1-{ \cos }^{3}\theta )}^{10}{ \cos }^{2}\theta \sin \theta d\theta[/latex]

33. [latex]\int ( \cos \theta -1){({ \cos }^{2}\theta -2 \cos \theta )}^{3} \sin \theta d\theta[/latex]

34. [latex]\int ({ \sin }^{2}\theta -2 \sin \theta ){({ \sin }^{3}\theta -3{ \sin }^{2}\theta )}^{3} \cos \theta d\theta[/latex]

In the following exercises, use a calculator to estimate the area under the curve using left Riemann sums with 50 terms, then use substitution to solve for the exact answer.

35. [T][latex]y=3{(1-x)}^{2}[/latex] over [latex]\left[0,2\right][/latex]

36. [T][latex]y=x{(1-{x}^{2})}^{3}[/latex] over [latex]\left[-1,2\right][/latex]

37. [T][latex]y= \sin x{(1- \cos x)}^{2}[/latex] over [latex]\left[0,\pi \right][/latex]

38. [T][latex]y=\frac{x}{{({x}^{2}+1)}^{2}}[/latex] over [latex]\left[-1,1\right][/latex]

In the following exercises, use a change of variables to evaluate the definite integral.

39. [latex]{\int }_{0}^{1}x\sqrt{1-{x}^{2}}dx[/latex]

40. [latex]{\int }_{0}^{1}\frac{x}{\sqrt{1+{x}^{2}}}dx[/latex]

41. [latex]{\int }_{0}^{2}\frac{t}{\sqrt{5+{t}^{2}}}dt[/latex]

42. [latex]{\int }_{0}^{1}\frac{t}{\sqrt{1+{t}^{3}}}dt[/latex]

43. [latex]{\int }_{0}^{\pi \text{/}4}{ \sec }^{2}\theta \tan \theta d\theta[/latex]

44. [latex]{\int }_{0}^{\pi \text{/}4}\frac{ \sin \theta }{{ \cos }^{4}\theta }d\theta[/latex]

In the following exercises, evaluate the indefinite integral [latex]\int f(x)dx[/latex] with constant [latex]C=0[/latex] using [latex]u[/latex]-substitution. Then, graph the function and the antiderivative over the indicated interval. If possible, estimate a value of C that would need to be added to the antiderivative to make it equal to the definite integral [latex]F(x)={\int }_{a}^{x}f(t)dt,[/latex] with [latex]a[/latex] the left endpoint of the given interval.

45. [T][latex]\int (2x+1){e}^{{x}^{2}+x-6}dx[/latex] over [latex]\left[-3,2\right][/latex]

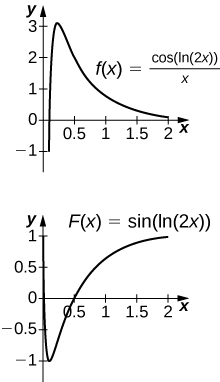
46. [T][latex]\int \frac{ \cos (\text{ln}(2x))}{x}dx[/latex] on [latex]\left[0,2\right][/latex]

47. [T][latex]\int \frac{3{x}^{2}+2x+1}{\sqrt{{x}^{3}+{x}^{2}+x+4}}dx[/latex] over [latex]\left[-1,2\right][/latex]

48. [T][latex]\int \frac{ \sin x}{{ \cos }^{3}x}dx[/latex] over [latex]\left[-\frac{\pi }{3},\frac{\pi }{3}\right][/latex]

49. [T][latex]\int (x+2){e}^{\text{−}{x}^{2}-4x+3}dx[/latex] over [latex]\left[-5,1\right][/latex]

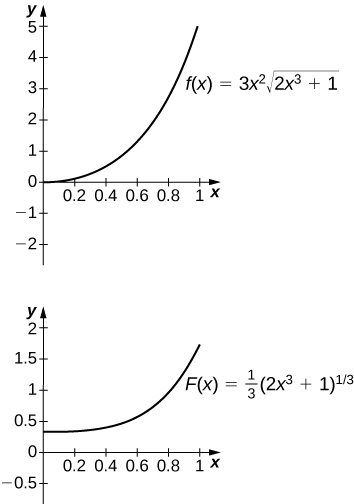
50. [T][latex]\int 3{x}^{2}\sqrt{2{x}^{3}+1}dx[/latex] over [latex]\left[0,1\right][/latex]

51. If [latex]h(a)=h(b)[/latex] in [latex]{\int }_{a}^{b}g\text{'}(h(x))h(x)dx,[/latex] what can you say about the value of the integral?

52. Is the substitution [latex]u=1-{x}^{2}[/latex] in the definite integral [latex]{\int }_{0}^{2}\frac{x}{1-{x}^{2}}dx[/latex] okay? If not, why not?

In the following exercises, use a change of variables to show that each definite integral is equal to zero.

53. [latex]{\int }_{0}^{\pi }{ \cos }^{2}(2\theta ) \sin (2\theta )d\theta[/latex]

54. [latex]{\int }_{0}^{\sqrt{\pi }}t \cos ({t}^{2}) \sin ({t}^{2})dt[/latex]

55. [latex]{\int }_{0}^{1}(1-2t)dt[/latex]

56. [latex]{\int }_{0}^{1}\frac{1-2t}{(1+{(t-\frac{1}{2})}^{2})}dt[/latex]

57. [latex]{\int }_{0}^{\pi } \sin ({(t-\frac{\pi }{2})}^{3}) \cos (t-\frac{\pi }{2})dt[/latex]

58. [latex]{\int }_{0}^{2}(1-t) \cos (\pi t)dt[/latex]

59. [latex]{\int }_{\pi \text{/}4}^{3\pi \text{/}4}{ \sin }^{2}t \cos tdt[/latex]

60. Show that the average value of [latex]f(x)[/latex] over an interval [latex]\left[a,b\right][/latex] is the same as the average value of [latex]f(cx)[/latex] over the interval [latex]\left[\frac{a}{c},\frac{b}{c}\right][/latex] for [latex]c>0.[/latex]

61. Find the area under the graph of [latex]f(t)=\frac{t}{{(1+{t}^{2})}^{a}}[/latex] between [latex]t=0[/latex] and [latex]t=x[/latex] where [latex]a>0[/latex] and [latex]a\ne 1[/latex] is fixed, and evaluate the limit as [latex]x\to \infty .[/latex]

62. Find the area under the graph of [latex]g(t)=\frac{t}{{(1-{t}^{2})}^{a}}[/latex] between [latex]t=0[/latex] and [latex]t=x,[/latex] where [latex]00[/latex] is fixed. Evaluate the limit as [latex]x\to 1.[/latex]

63. The area of a semicircle of radius 1 can be expressed as [latex]{\int }_{-1}^{1}\sqrt{1-{x}^{2}}dx.[/latex] Use the substitution [latex]x= \cos t[/latex] to express the area of a semicircle as the integral of a trigonometric function. You do not need to compute the integral.

64. The area of the top half of an ellipse with a major axis that is the [latex]x[/latex]-axis from [latex]x=-1[/latex] to [latex]a[/latex] and with a minor axis that is the [latex]y[/latex]-axis from [latex]y=\text{−}b[/latex] to [latex]b[/latex] can be written as [latex]{\int }_{\text{−}a}^{a}b\sqrt{1-\frac{{x}^{2}}{{a}^{2}}}dx.[/latex] Use the substitution [latex]x=a \cos t[/latex] to express this area in terms of an integral of a trigonometric function. You do not need to compute the integral.

65. [T] The following graph is of a function of the form [latex]f(t)=a \sin (nt)+b \sin (mt).[/latex] Estimate the coefficients [latex]a[/latex] and [latex]b[/latex], and the frequency parameters [latex]n[/latex] and [latex]m[/latex]. Use these estimates to approximate [latex]{\int }_{0}^{\pi }f(t)dt.[/latex]

A graph of a function of the given form over [0, 2pi], which has six turning points. They are located at just before pi/4, just after pi/2, between 3pi/4 and pi, between pi and 5pi/4, just before 3pi/2, and just after 7pi/4 at about 3, -2, 1, -1, 2, and -3. It begins at the origin and ends at (2pi, 0). It crosses the x axis between pi/4 and pi/2, just before 3pi/4, pi, just after 5pi/4, and between 3pi/2 and 4pi/4.

66. [T] The following graph is of a function of the form [latex]f(x)=a \cos (nt)+b \cos (mt).[/latex] Estimate the coefficients [latex]a[/latex] and [latex]b[/latex] and the frequency parameters [latex]n[/latex] and [latex]m[/latex]. Use these estimates to approximate [latex]{\int }_{0}^{\pi }f(t)dt.[/latex]

The graph of a function of the given form over [0, 2pi]. It begins at (0,1) and ends at (2pi, 1). It has five turning points, located just after pi/4, between pi/2 and 3pi/4, pi, between 5pi/4 and 3pi/2, and just before 7pi/4 at about -1.5, 2.5, -3, 2.5, and -1. It crosses the x axis between 0 and pi/4, just before pi/2, just after 3pi/4, just before 5pi/4, just after 3pi/2, and between 7pi/4 and 2pi.

Glossary

change of variables
the substitution of a variable, such as [latex]u[/latex], for an expression in the integrand
integration by substitution
a technique for integration that allows integration of functions that are the result of a chain-rule derivative