Proofs, Identities, and Toolkit Functions

Appendix

Important Proofs and Derivations

Product Rule

[latex]{\mathrm{log}}_{a}xy={\mathrm{log}}_{a}x+{\mathrm{log}}_{a}y[/latex]

Proof:

Let[latex]\,m={\mathrm{log}}_{a}x\,[/latex]and[latex]\,n={\mathrm{log}}_{a}y.[/latex]

Write in exponent form.

[latex]x={a}^{m}\,[/latex]and[latex]\,y={a}^{n}.[/latex]

Multiply.

[latex]xy={a}^{m}{a}^{n}={a}^{m+n}[/latex]

[latex]\begin{array}{ccc}\hfill {a}^{m+n}& =& xy\hfill \\ \hfill {\mathrm{log}}_{a}\left(xy\right)& =& m+n\hfill \\ & =& {\mathrm{log}}_{a}x+{\mathrm{log}}_{b}y\hfill \end{array}[/latex]

Change of Base Rule

[latex]\begin{array}{l}\hfill \\ {\mathrm{log}}_{a}b=\frac{{\mathrm{log}}_{c}b}{{\mathrm{log}}_{c}a}\hfill \\ {\mathrm{log}}_{a}b=\frac{1}{{\mathrm{log}}_{b}a}\hfill \end{array}[/latex]

where[latex]\,x\,[/latex]and[latex]\,y\,[/latex]are positive, and[latex]\,a>0,a\ne 1.[/latex]

Proof:

Let[latex]\,x={\mathrm{log}}_{a}b.[/latex]

Write in exponent form.

[latex]{a}^{x}=b[/latex]

Take the[latex]\,{\mathrm{log}}_{c}\,[/latex]of both sides.

[latex]\begin{array}{ccc}\hfill {\mathrm{log}}_{c}{a}^{x}& =& {\mathrm{log}}_{c}b\hfill \\ \hfill x{\mathrm{log}}_{c}a& =& {\mathrm{log}}_{c}b\hfill \\ \hfill x& =& \frac{{\mathrm{log}}_{c}b}{{\mathrm{log}}_{c}a}\hfill \\ \hfill {\mathrm{log}}_{a}b& =& \frac{{\mathrm{log}}_{c}b}{{\mathrm{log}}_{a}b}\hfill \end{array}[/latex]

When[latex]\,c=b,[/latex]

[latex]{\mathrm{log}}_{a}b=\frac{{\mathrm{log}}_{b}b}{{\mathrm{log}}_{b}a}=\frac{1}{{\mathrm{log}}_{b}a}[/latex]

Heron’s Formula

[latex]A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}[/latex]

where[latex]\,s=\frac{a+b+c}{2}[/latex]

Proof:

Let[latex]\,a,[/latex][latex]b,[/latex]and[latex]\,c\,[/latex]be the sides of a triangle, and[latex]\,h\,[/latex]be the height.

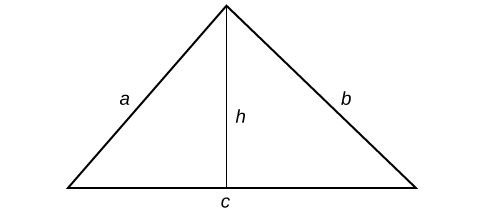
A triangle with sides labeled: a, b and c. A line runs through the center of the triangle, bisecting the top angle; this line is labeled: h.

Figure 1.

So[latex]\,s=\frac{a+b+c}{2}[/latex].

We can further name the parts of the base in each triangle established by the height such that[latex]\,p+q=c.[/latex]

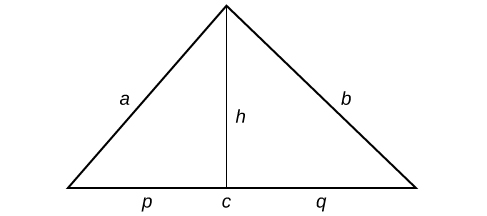
A triangle with sides labeled: a, b, and c. A line runs through the center of the triangle bisecting the angle at the top; this line is labeled: h. The two new line segments on the base of the triangle are labeled: p and q.

Figure 2.

Using the Pythagorean Theorem,[latex]\,{h}^{2}+{p}^{2}={a}^{2}\,[/latex]and[latex]\,{h}^{2}+{q}^{2}={b}^{2}.[/latex]

Since[latex]\,q=c-p,[/latex]then[latex]\,{q}^{2}={\left(c-p\right)}^{2}.\,[/latex]Expanding, we find that[latex]\,{q}^{2}={c}^{2}-2cp+{p}^{2}.[/latex]

We can then add[latex]\,{h}^{2}\,[/latex]to each side of the equation to get[latex]\,{h}^{2}+{q}^{2}={h}^{2}+{c}^{2}-2cp+{p}^{2}.[/latex]

Substitute this result into the equation[latex]\,{h}^{2}+{q}^{2}={b}^{2}\,[/latex]yields[latex]\,{b}^{2}={h}^{2}+{c}^{2}-2cp+{p}^{2}.[/latex]

Then replacing[latex]\,{h}^{2}+{p}^{2}\,[/latex]with[latex]\,{a}^{2}\,[/latex]gives[latex]\,{b}^{2}={a}^{2}-2cp+{c}^{2}.[/latex]

Solve for[latex]\,p\,[/latex]to get

[latex]p=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2c}[/latex]

Since[latex]\,{h}^{2}={a}^{2}-{p}^{2},[/latex]we get an expression in terms of[latex]\,a,[/latex][latex]b,[/latex]and [latex]\,c.[/latex]

[latex]\begin{array}{ccc}\hfill {h}^{2}& =& {a}^{2}-{p}^{2}\hfill \\ & =& \left(a+p\right)\left(a-p\right)\hfill \\ & =& \left[a+\frac{\left({a}^{2}+{c}^{2}-{b}^{2}\right)}{2c}\right]\left[a-\frac{\left({a}^{2}+{c}^{2}-{b}^{2}\right)}{2c}\right]\hfill \\ & =& \frac{\left(2ac+{a}^{2}+{c}^{2}-{b}^{2}\right)\left(2ac-{a}^{2}-{c}^{2}+{b}^{2}\right)}{4{c}^{2}}\hfill \\ & =& \frac{\left({\left(a+c\right)}^{2}-{b}^{2}\right)\left({b}^{2}-{\left(a-c\right)}^{2}\right)}{4{c}^{2}}\hfill \\ & =& \frac{\left(a+b+c\right)\left(a+c-b\right)\left(b+a-c\right)\left(b-a+c\right)}{4{c}^{2}}\hfill \\ & =& \frac{\left(a+b+c\right)\left(-a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)}{4{c}^{2}}\hfill \\ & =& \frac{2s\cdot \left(2s-a\right)\cdot \left(2s-b\right)\left(2s-c\right)}{4{c}^{2}}\hfill \end{array}[/latex]

Therefore,

[latex]\begin{array}{ccc}\hfill {h}^{2}& =& \frac{4s\left(s-a\right)\left(s-b\right)\left(s-c\right)}{{c}^{2}}\hfill \\ \hfill h& =& \frac{2\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}{c}\hfill \end{array}[/latex]

And since[latex]\,A=\frac{1}{2}ch,[/latex]then

[latex]\begin{array}{ccc}\hfill A& =& \frac{1}{2}c\frac{2\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}{c}\hfill \\ & =& \sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}\hfill \end{array}[/latex]

Properties of the Dot Product

[latex]u·v=v·u[/latex]

Proof:

[latex]\begin{array}{cc}\hfill u·v& =〈{u}_{1},{u}_{2},...{u}_{n}〉·〈{v}_{1},{v}_{2},...{v}_{n}〉\hfill \\ & ={u}_{1}{v}_{1}+{u}_{2}{v}_{2}+...+{u}_{n}{v}_{n}\hfill \\ & ={v}_{1}{u}_{1}+{v}_{2}{u}_{2}+...+{v}_{n}{v}_{n}\hfill \\ & =〈{v}_{1},{v}_{2},...{v}_{n}〉·〈{u}_{1},{u}_{2},...{u}_{n}〉\hfill \\ & =v·u\hfill \end{array}[/latex]

[latex]u·\left(v+w\right)=u·v+u·w[/latex]

Proof:

[latex]\begin{array}{cc}\hfill u·\left(v+w\right)& =〈{u}_{1},{u}_{2},...{u}_{n}〉·\left(〈{v}_{1},{v}_{2},...{v}_{n}〉+〈{w}_{1},{w}_{2},...{w}_{n}〉\right)\hfill \\ & =〈{u}_{1},{u}_{2},...{u}_{n}〉·〈{v}_{1}+{w}_{1},{v}_{2}+{w}_{2},...{v}_{n}+{w}_{n}〉\hfill \\ & =〈{u}_{1}\left({v}_{1}+{w}_{1}\right),{u}_{2}\left({v}_{2}+{w}_{2}\right),...{u}_{n}\left({v}_{n}+{w}_{n}\right)〉\hfill \\ & =〈{u}_{1}{v}_{1}+{u}_{1}{w}_{1},{u}_{2}{v}_{2}+{u}_{2}{w}_{2},...{u}_{n}{v}_{n}+{u}_{n}{w}_{n}〉\hfill \\ & =〈{u}_{1}{v}_{1},{u}_{2}{v}_{2},...,{u}_{n}{v}_{n}〉+〈{u}_{1}{w}_{1},{u}_{2}{w}_{2},...,{u}_{n}{w}_{n}〉\hfill \\ & =〈{u}_{1},{u}_{2},...{u}_{n}〉·〈{v}_{1},{v}_{2},...{v}_{n}〉+〈{u}_{1},{u}_{2},...{u}_{n}〉·〈{w}_{1},{w}_{2},...{w}_{n}〉\hfill \\ & =u·v+u·w\hfill \end{array}[/latex]

[latex]u·u={|u|}^{2}[/latex]

Proof:

[latex]\begin{array}{cc}\hfill u·u& =〈{u}_{1},{u}_{2},...{u}_{n}〉·〈{u}_{1},{u}_{2},...{u}_{n}〉\hfill \\ & ={u}_{1}{u}_{1}+{u}_{2}{u}_{2}+...+{u}_{n}{u}_{n}\hfill \\ & ={u}_{1}{}^{2}+{u}_{2}{}^{2}+...+{u}_{n}{}^{2}\hfill \\ & =|〈{u}_{1},{u}_{2},...{u}_{n}〉{|}^{2}\hfill \\ & =v·u\hfill \end{array}[/latex]

Standard Form of the Ellipse centered at the Origin

[latex]1=\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}[/latex]

Derivation

An ellipse consists of all the points for which the sum of distances from two foci is constant:

[latex]\sqrt{{\left(x-\left(-c\right)\right)}^{2}+{\left(y-0\right)}^{2}}+\sqrt{{\left(x-c\right)}^{2}+{\left(y-0\right)}^{2}}=\text{constant}[/latex]

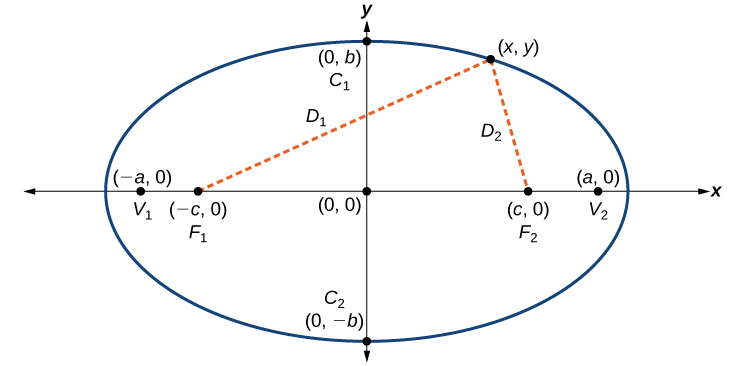
An ellipse centered at the origin on an x, y-coordinate plane. Points C1 and C2 are plotted at the points (0, b) and (0, -b) respectively; these points appear on the ellipse. Points V1 and V2 are plotted at the points (-a, 0) and (a, 0) respectively; these points appear on the ellipse. Points F1 and F2 are plotted at the points (-c, 0) and (c, 0) respectively; these points appear on the x-axis, but not the ellipse. The point (x, y) appears on the ellipse in the first quadrant. Dotted lines extend from F1 and F2 to the point (x, y).

Figure 3.

Consider a vertex.

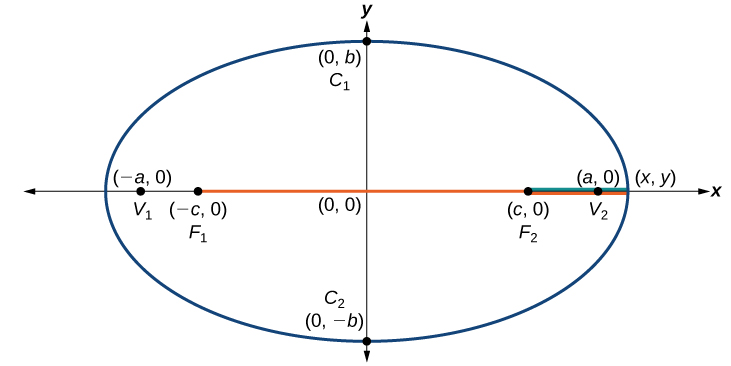
An ellipse centered at the origin. The points C1 and C2 are plotted at the points (0, b) and (0, -b) respectively; these points are on the ellipse. The points V1 and V2 are plotted at the points (-a, 0) and (a, 0) respectively; these points are on the ellipse. The points F1 and F2 are plotted at the points (-c, 0) and (c, 0) respectively; these points are on the x-axis and not on the ellipse. A line extends from the point F1 to a point (x, y) which is at the point (a, 0). A line extends from the point F2 to the point (x, y) as well.

Figure 4.

Then,[latex]\,\sqrt{{\left(x-\left(-c\right)\right)}^{2}+{\left(y-0\right)}^{2}}+\sqrt{{\left(x-c\right)}^{2}+{\left(y-0\right)}^{2}}=2a[/latex]

Consider a covertex.

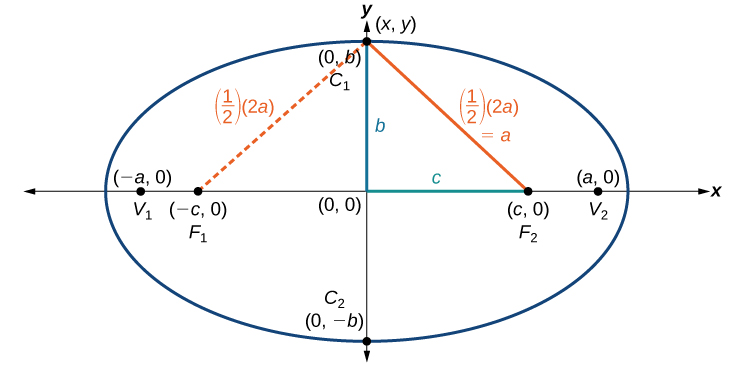
An ellipse centered at the origin. The points C1 and C2 are plotted at the points (0, b) and (0, -b) respectively; these points are on the ellipse. The points V1 and V2 are plotted at the points (-a, 0) and (a, 0) respectively; these points are on the ellipse. The points F1 and F2 are plotted at the points (-c, 0) and (c, 0) respectively; these points are on the x-axis and not on the ellipse. There is a point (x, y) which is plotted at (0, b). A line extends from the origin to the point (c, 0), this line is labeled: c. A line extends from the origin to the point (x, y), this line is labeled: b. A line extends from the point (c, 0) to the point (x, y); this line is labeled: (1/2)(2a)=a. A dotted line extends from the point (-c, 0) to the point (x, y); this line is labeled: (1/2)(2a)=a.

Figure 5.

Then[latex]\,{b}^{2}+{c}^{2}={a}^{2}.[/latex]

[latex]\begin{array}{ccc}\hfill \sqrt{{\left(x-\left(-c\right)\right)}^{2}+{\left(y-0\right)}^{2}}+\sqrt{{\left(x-c\right)}^{2}+{\left(y-0\right)}^{2}}& =& 2a\hfill \\ \hfill \sqrt{{\left(x+c\right)}^{2}+{y}^{2}}& =& 2a-\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill \\ \hfill {\left(x+c\right)}^{2}+{y}^{2}& =& {\left(2a-\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\right)}^{2}\hfill \\ \hfill {x}^{2}+2cx+{c}^{2}+{y}^{2}& =& 4{a}^{2}-4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}+{\left(x-c\right)}^{2}+{y}^{2}\hfill \\ \hfill {x}^{2}+2cx+{c}^{2}+{y}^{2}& =& 4{a}^{2}-4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}+{x}^{2}-2cx+{y}^{2}\hfill \\ \hfill 2cx& =& 4{a}^{2}-4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}-2cx\hfill \\ \hfill 4cx-4{a}^{2}& =& 4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill \\ \hfill -\frac{1}{4a}\left(4cx-4{a}^{2}\right)& =& \sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill \\ \hfill a-\frac{c}{a}x& =& \sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill \\ \hfill {a}^{2}-2xc+\frac{{c}^{2}}{{a}^{2}}{x}^{2}& =& {\left(x-c\right)}^{2}+{y}^{2}\hfill \\ \hfill {a}^{2}-2xc+\frac{{c}^{2}}{{a}^{2}}{x}^{2}& =& {x}^{2}-2xc+{c}^{2}+{y}^{2}\hfill \\ \hfill {a}^{2}+\frac{{c}^{2}}{{a}^{2}}{x}^{2}& =& {x}^{2}+{c}^{2}+{y}^{2}\hfill \\ \hfill {a}^{2}+\frac{{c}^{2}}{{a}^{2}}{x}^{2}& =& {x}^{2}+{c}^{2}+{y}^{2}\hfill \\ \hfill {a}^{2}-{c}^{2}& =& {x}^{2}-\frac{{c}^{2}}{{a}^{2}}{x}^{2}+{y}^{2}\hfill \\ \hfill {a}^{2}-{c}^{2}& =& {x}^{2}\left(1-\frac{{c}^{2}}{{a}^{2}}\right)+{y}^{2}\hfill \end{array}[/latex]

Let[latex]\,1=\frac{{a}^{2}}{{a}^{2}}.[/latex]

[latex]\begin{array}{ccc}\hfill {a}^{2}-{c}^{2}& =& {x}^{2}\left(\frac{{a}^{2}-{c}^{2}}{{a}^{2}}\right)+{y}^{2}\hfill \\ \hfill 1& =& \frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-{c}^{2}}\hfill \end{array}[/latex]

Because[latex]\,{b}^{2}+{c}^{2}={a}^{2},[/latex]then[latex]\,{b}^{2}={a}^{2}-{c}^{2}.[/latex]

[latex]\begin{array}{ccc}\hfill 1& =& \frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-{c}^{2}}\hfill \\ \hfill 1& =& \frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}\hfill \end{array}[/latex]

Standard Form of the Hyperbola

[latex]1=\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}[/latex]

Derivation

A hyperbola is the set of all points in a plane such that the absolute value of the difference of the distances between two fixed points is constant.

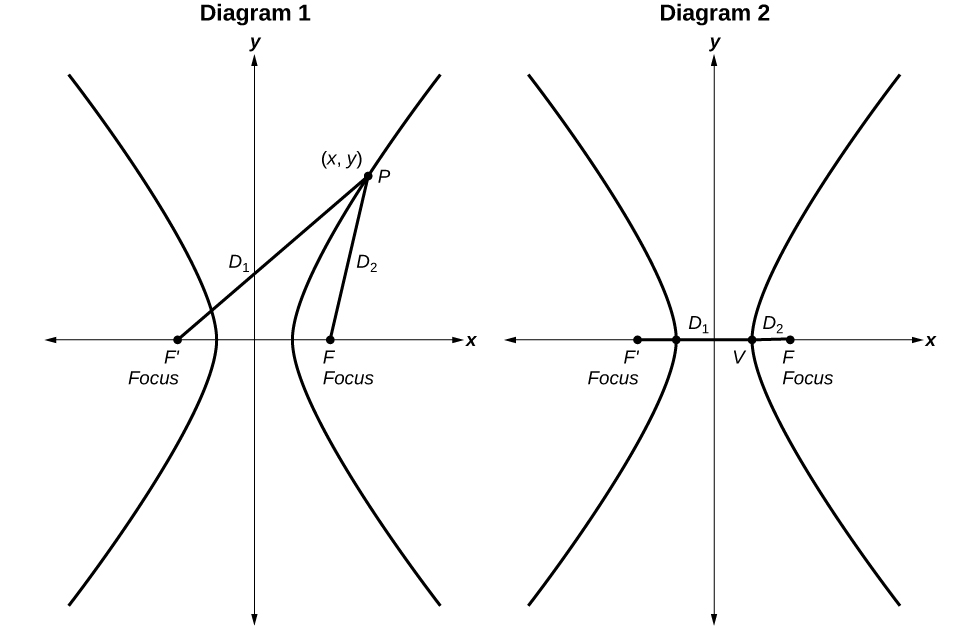
Side-by-side graphs of hyperbole. In Diagram 1: The foci F’ and F are labeled and can be found a little in front of the opening of the hyperbola. A point P at (x,y) on the right curve is labeled. A line extends from the F’ focus to the point P labeled: D1. A line extends from the F focus to the point P labeled: D2. In Diagram 2: The foci F’ and F are labeled and can be found a little in front of the opening of the hyperbola. A point V is labeled at the vertex of the right hyperbola. A line extends from the F’ focus to the point V labeled: D1. A line extends from the F focus to the point V labeled: D2.

Figure 6.

Diagram 1: The difference of the distances from Point P to the foci is constant:

[latex]\sqrt{{\left(x-\left(-c\right)\right)}^{2}+{\left(y-0\right)}^{2}}-\sqrt{{\left(x-c\right)}^{2}+{\left(y-0\right)}^{2}}=\text{constant}[/latex]

Diagram 2: When the point is a vertex, the difference is[latex]\,2a.[/latex]

[latex]\sqrt{{\left(x-\left(-c\right)\right)}^{2}+{\left(y-0\right)}^{2}}-\sqrt{{\left(x-c\right)}^{2}+{\left(y-0\right)}^{2}}=2a[/latex]

[latex]\begin{array}{ccc}\hfill \sqrt{{\left(x-\left(-c\right)\right)}^{2}+{\left(y-0\right)}^{2}}-\sqrt{{\left(x-c\right)}^{2}+{\left(y-0\right)}^{2}}& =& 2a\hfill \\ \hfill \sqrt{{\left(x+c\right)}^{2}+{y}^{2}}-\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}& =& 2a\hfill \\ \hfill \sqrt{{\left(x+c\right)}^{2}+{y}^{2}}& =& 2a+\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill \\ \hfill {\left(x+c\right)}^{2}+{y}^{2}& =& \left(2a+\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\right)\hfill \\ \hfill {x}^{2}+2cx+{c}^{2}+{y}^{2}& =& 4{a}^{2}+4a\sqrt{{\left(x-c\right)}^{2}}+{y}^{2}\hfill \\ \hfill {x}^{2}+2cx+{c}^{2}+{y}^{2}& =& 4{a}^{2}+4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}+{x}^{2}-2cx+{y}^{2}\hfill \\ \hfill 2cx& =& 4{a}^{2}+4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}-2cx\hfill \\ \hfill 4cx-4{a}^{2}& =& 4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill \\ \hfill cx-{a}^{2}& =& a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill \\ \hfill {\left(cx-{a}^{2}\right)}^{2}& =& {a}^{2}\left({\left(x-c\right)}^{2}+{y}^{2}\right)\hfill \\ \hfill {c}^{2}{x}^{2}-2{a}^{2}{c}^{2}{x}^{2}+{a}^{4}& =& {a}^{2}{x}^{2}-2{a}^{2}{c}^{2}{x}^{2}+{a}^{2}{c}^{2}+{a}^{2}{y}^{2}\hfill \\ \hfill {c}^{2}{x}^{2}+{a}^{4}& =& {a}^{2}{x}^{2}+{a}^{2}{c}^{2}+{a}^{2}{y}^{2}\hfill \\ \hfill {a}^{4}-{a}^{2}{c}^{2}& =& {a}^{2}{x}^{2}-{c}^{2}{x}^{2}+{a}^{2}{y}^{2}\hfill \\ \hfill {a}^{2}\left({a}^{2}-{c}^{2}\right)& =& \left({a}^{2}-{c}^{2}\right){x}^{2}+{a}^{2}{y}^{2}\hfill \\ \hfill {a}^{2}\left({a}^{2}-{c}^{2}\right)& =& \left({c}^{2}-{a}^{2}\right){x}^{2}-{a}^{2}{y}^{2}\hfill \end{array}[/latex]

Define[latex]\,b\,[/latex]as a positive number such that[latex]\,{b}^{2}={c}^{2}-{a}^{2}.[/latex]

[latex]\begin{array}{ccc}\hfill {a}^{2}{b}^{2}& =& {b}^{2}{x}^{2}-{a}^{2}{y}^{2}\hfill \\ \hfill \frac{{a}^{2}{b}^{2}}{{a}^{2}{b}^{2}}& =& \frac{{b}^{2}{x}^{2}}{{a}^{2}{b}^{2}}-\frac{{a}^{2}{y}^{2}}{{a}^{2}{b}^{2}}\hfill \\ \hfill 1& =& \frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}\hfill \end{array}[/latex]

Trigonometric Identities

Pythagorean Identity [latex]\begin{array}{l}{\mathrm{cos}}^{2}t+{\mathrm{sin}}^{2}t=1\\ 1+{\mathrm{tan}}^{2}t={\mathrm{sec}}^{2}t\\ 1+{\mathrm{cot}}^{2}t={\mathrm{csc}}^{2}t\end{array}[/latex]
Even-Odd Identities [latex]\begin{array}{l}\mathrm{cos}\left(-t\right)=cos\,t\hfill \\ \mathrm{sec}\left(-t\right)=\mathrm{sec}\,t\hfill \\ \mathrm{sin}\left(-t\right)=-\mathrm{sin}\,t\hfill \\ \mathrm{tan}\left(-t\right)=-\mathrm{tan}\,t\hfill \\ \mathrm{csc}\left(-t\right)=-\mathrm{csc}\,t\hfill \\ \mathrm{cot}\left(-t\right)=-\mathrm{cot}\,t\hfill \end{array}[/latex]
Cofunction Identities [latex]\begin{array}{l}\hfill \\ \mathrm{cos}\,t=\mathrm{sin}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{sin}\,t=\mathrm{cos}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{tan}\,t=\mathrm{cot}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{cot}\,t=\mathrm{tan}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{sec}\,t=\mathrm{csc}\left(\frac{\pi }{2}-t\right)\hfill \\ \mathrm{csc}\,t=\mathrm{sec}\left(\frac{\pi }{2}-t\right)\hfill \end{array}[/latex]
Fundamental Identities [latex]\begin{array}{l}\mathrm{tan}\,t=\frac{\mathrm{sin}\,t}{\mathrm{cos}\,t}\hfill \\ \mathrm{sec}\,t=\frac{1}{\mathrm{cos}\,t}\hfill \\ \mathrm{csc}\,t=\frac{1}{\mathrm{sin}\,t}\hfill \\ cot\,t=\frac{1}{\text{tan}\,t}=\frac{\text{cos}\,t}{\text{sin}\,t}\hfill \end{array}[/latex]
Sum and Difference Identities [latex]\begin{array}{l}\mathrm{cos}\left(\alpha +\beta \right)=\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta \hfill \\ \mathrm{cos}\left(\alpha -\beta \right)=\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta +\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta \hfill \\ \mathrm{sin}\left(\alpha +\beta \right)=\mathrm{sin}\,\alpha \,\mathrm{cos}\,\beta +\mathrm{cos}\,\alpha \,\mathrm{sin}\,\beta \hfill \\ \mathrm{sin}\left(\alpha -\beta \right)=\mathrm{sin}\,\alpha \,\mathrm{cos}\,\beta -\mathrm{cos}\,\alpha \,\mathrm{sin}\,\beta \hfill \\ \mathrm{tan}\left(\alpha +\beta \right)=\frac{\mathrm{tan}\,\alpha +\mathrm{tan}\,\beta }{1-\mathrm{tan}\,\alpha \,\mathrm{tan}\,\beta }\hfill \\ \mathrm{tan}\left(\alpha -\beta \right)=\frac{\mathrm{tan}\,\alpha -\mathrm{tan}\,\beta }{1+\mathrm{tan}\,\alpha \,\mathrm{tan}\,\beta }\hfill \end{array}[/latex]
Double-Angle Formulas [latex]\begin{array}{l}\mathrm{sin}\left(2\theta \right)=2\mathrm{sin}\,\theta \,\mathrm{cos}\,\theta \hfill \\ \mathrm{cos}\left(2\theta \right)={\mathrm{cos}}^{2}\theta -{\mathrm{sin}}^{2}\theta \hfill \\ \mathrm{cos}\left(2\theta \right)=1-2{\mathrm{sin}}^{2}\theta \hfill \\ \mathrm{cos}\left(2\theta \right)=2{\mathrm{cos}}^{2}\theta -1\hfill \\ \mathrm{tan}\left(2\theta \right)=\frac{2\mathrm{tan}\,\theta }{1-{\mathrm{tan}}^{2}\theta }\hfill \end{array}[/latex]
Half-Angle Formulas [latex]\begin{array}{l}\hfill \\ \mathrm{sin}\frac{\alpha }{2}=±\sqrt{\frac{1-\mathrm{cos}\,\alpha }{2}}\hfill \\ \mathrm{cos}\frac{\alpha }{2}=±\sqrt{\frac{1+\mathrm{cos}\,\alpha }{2}}\hfill \\ \mathrm{tan}\frac{\alpha }{2}=±\sqrt{\frac{1-\mathrm{cos}\,\alpha }{1+\mathrm{cos}\,\alpha }}\hfill \\ \mathrm{tan}\frac{\alpha }{2}=\frac{\mathrm{sin}\,\alpha }{1+\mathrm{cos}\,\alpha }\hfill \\ \mathrm{tan}\frac{\alpha }{2}=\frac{1-\mathrm{cos}\,\alpha }{\mathrm{sin}\,\alpha }\hfill \end{array}[/latex]
Reduction Formulas [latex]\begin{array}{l}\hfill \\ {\mathrm{sin}}^{2}\theta =\frac{1-\mathrm{cos}\left(2\theta \right)}{2}\hfill \\ {\mathrm{cos}}^{2}\theta =\frac{1+\mathrm{cos}\left(2\theta \right)}{2}\hfill \\ {\mathrm{tan}}^{2}\theta =\frac{1-\mathrm{cos}\left(2\theta \right)}{1+\mathrm{cos}\left(2\theta \right)}\hfill \end{array}[/latex]
Product-to-Sum Formulas [latex]\begin{array}{l}\hfill \\ \mathrm{cos}\alpha \mathrm{cos}\beta =\frac{1}{2}\left[\mathrm{cos}\left(\alpha -\beta \right)+\mathrm{cos}\left(\alpha +\beta \right)\right]\hfill \\ \mathrm{sin}\alpha \mathrm{cos}\beta =\frac{1}{2}\left[\mathrm{sin}\left(\alpha +\beta \right)+\mathrm{sin}\left(\alpha -\beta \right)\right]\hfill \\ \mathrm{sin}\alpha \mathrm{sin}\beta =\frac{1}{2}\left[\mathrm{cos}\left(\alpha -\beta \right)-\mathrm{cos}\left(\alpha +\beta \right)\right]\hfill \\ \mathrm{cos}\alpha \mathrm{sin}\beta =\frac{1}{2}\left[\mathrm{sin}\left(\alpha +\beta \right)-\mathrm{sin}\left(\alpha -\beta \right)\right]\hfill \end{array}[/latex]
Sum-to-Product Formulas [latex]\begin{array}{l}\hfill \\ \mathrm{sin}\alpha +\mathrm{sin}\beta =2\mathrm{sin}\left(\frac{\alpha +\beta }{2}\right)\mathrm{cos}\left(\frac{\alpha -\beta }{2}\right)\hfill \\ \mathrm{sin}\alpha -\mathrm{sin}\beta =2\mathrm{sin}\left(\frac{\alpha -\beta }{2}\right)\mathrm{cos}\left(\frac{\alpha +\beta }{2}\right)\hfill \\ \mathrm{cos}\alpha -\mathrm{cos}\beta =-2\mathrm{sin}\left(\frac{\alpha +\beta }{2}\right)\mathrm{sin}\left(\frac{\alpha -\beta }{2}\right)\hfill \\ \mathrm{cos}\alpha +\mathrm{cos}\beta =2\mathrm{cos}\left(\frac{\alpha +\beta }{2}\right)\mathrm{cos}\left(\frac{\alpha -\beta }{2}\right)\hfill \end{array}[/latex]
Law of Sines [latex]\begin{array}{l}\frac{\mathrm{sin}\,\alpha }{a}=\frac{\mathrm{sin}\,\beta }{b}=\frac{\mathrm{sin}\,\gamma }{c}\hfill \\ \frac{a}{\mathrm{sin}\,\alpha }=\frac{b}{\mathrm{sin}\,\beta }=\frac{c}{\mathrm{sin}\,\gamma }\hfill \end{array}[/latex]
Law of Cosines [latex]\begin{array}{c}{a}^{2}={b}^{2}+{c}^{2}-2bc\,\mathrm{cos}\,\alpha \\ {b}^{2}={a}^{2}+{c}^{2}-2ac\,\mathrm{cos}\,\beta \\ {c}^{2}={a}^{2}+{b}^{2}-2ab\,\text{cos}\,\gamma \end{array}[/latex]

ToolKit Functions

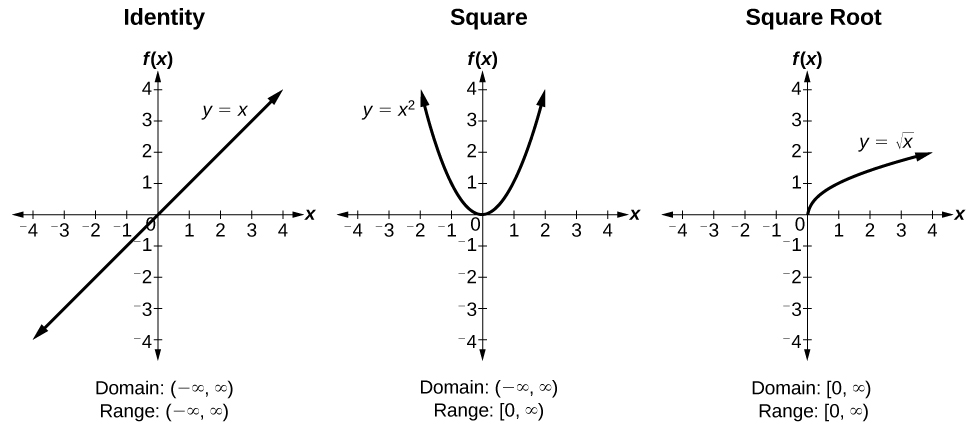
Three graphs side-by-side. From left to right, graph of the identify function, square function, and square root function. All three graphs extend from -4 to 4 on each axis.

Figure 7.

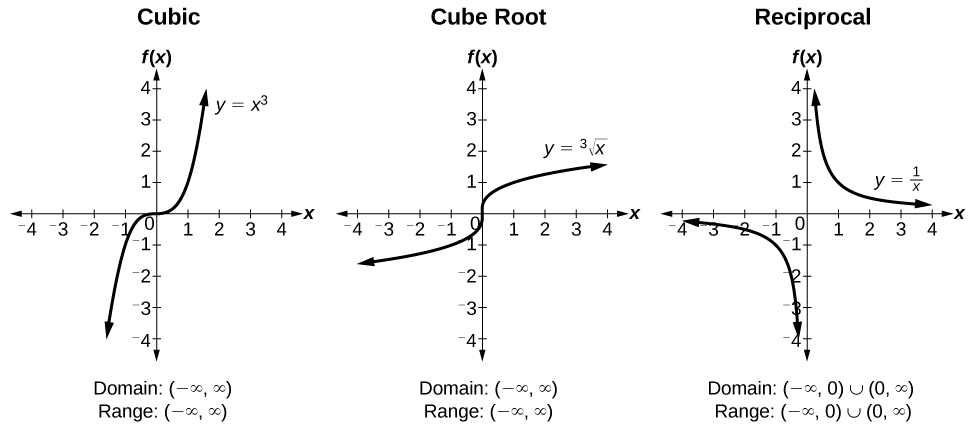
Three graphs side-by-side. From left to right, graph of the cubic function, cube root function, and reciprocal function. All three graphs extend from -4 to 4 on each axis.

Figure 8.

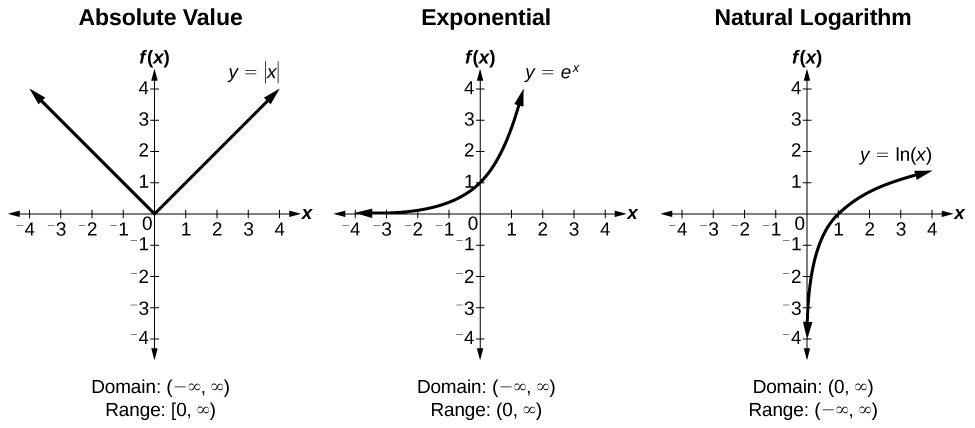
Three graphs side-by-side. From left to right, graph of the absolute value function, exponential function, and natural logarithm function. All three graphs extend from -4 to 4 on each axis.

Figure 9.

Trigonometric Functions

Unit Circle

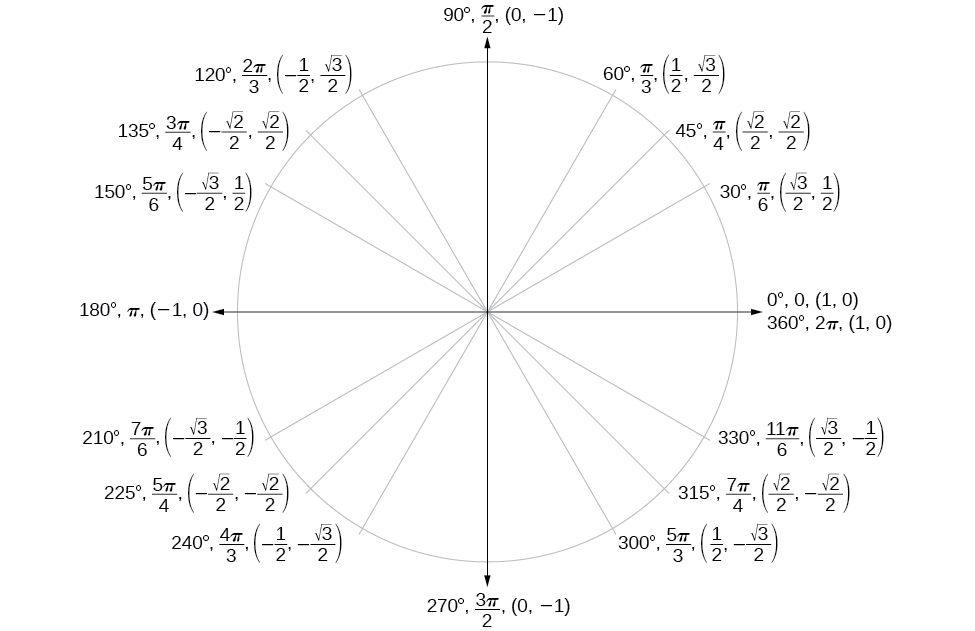
Graph of unit circle with angles in degrees, angles in radians, and points along the circle inscribed.

Figure 10.

Angle [latex]0[/latex] [latex]\frac{\pi }{6},\text{or 30}°[/latex] [latex]\frac{\pi }{4},\text{or 45}°[/latex] [latex]\frac{\pi }{3},\text{or 60}°[/latex] [latex]\frac{\pi }{2},\text{or 90}°[/latex]
Cosine 1 [latex]\frac{\sqrt{3}}{2}[/latex] [latex]\frac{\sqrt{2}}{2}[/latex] [latex]\frac{1}{2}[/latex] 0
Sine 0 [latex]\frac{1}{2}[/latex] [latex]\frac{\sqrt{2}}{2}[/latex] [latex]\frac{\sqrt{3}}{2}[/latex] 1
Tangent 0 [latex]\frac{\sqrt{3}}{3}[/latex] 1 [latex]\sqrt{3}[/latex] Undefined
Secant 1 [latex]\frac{2\sqrt{3}}{3}[/latex] [latex]\sqrt{2}[/latex] 2 Undefined
Cosecant Undefined 2 [latex]\sqrt{2}[/latex] [latex]\frac{2\sqrt{3}}{3}[/latex] 1
Cotangent Undefined [latex]\sqrt{3}[/latex] 1 [latex]\frac{\sqrt{3}}{3}[/latex] 0