Learning Objectives
- Graph exponential functions.
- Graph exponential functions using transformations.
As we discussed in the previous section, exponential functions are used for many real-world applications such as finance, forensics, computer science, and most of the life sciences. Working with an equation that describes a real-world situation gives us a method for making predictions. Most of the time, however, the equation itself is not enough. We learn a lot about things by seeing their pictorial representations, and that is exactly why graphing exponential equations is a powerful tool. It gives us another layer of insight for predicting future events.
Graphing Exponential Functions
Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form[latex]\,f\left(x\right)={b}^{x}\,[/latex]whose base is greater than one. We’ll use the function[latex]\,f\left(x\right)={2}^{x}.\,[/latex]Observe how the output values in (Figure) change as the input increases by[latex]\,1.[/latex]
| [latex]x[/latex] | [latex]-3[/latex] | [latex]-2[/latex] | [latex]-1[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] |
| [latex]f\left(x\right)={2}^{x}[/latex] | [latex]\frac{1}{8}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{2}[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]4[/latex] | [latex]8[/latex] |
Each output value is the product of the previous output and the base,[latex]\,2.\,[/latex]We call the base[latex]\,2\,[/latex]the constant ratio. In fact, for any exponential function with the form[latex]\,f\left(x\right)=a{b}^{x},[/latex][latex]\,b\,[/latex]is the constant ratio of the function. This means that as the input increases by 1, the output value will be the product of the base and the previous output, regardless of the value of[latex]\,a.[/latex]
Notice from the table that
- the output values are positive for all values of [latex]x;[/latex]
- as[latex]\,x\,[/latex]increases, the output values increase without bound; and
- as[latex]\,x\,[/latex]decreases, the output values grow smaller, approaching zero.
(Figure) shows the exponential growth function [latex]\,f\left(x\right)={2}^{x}.[/latex]
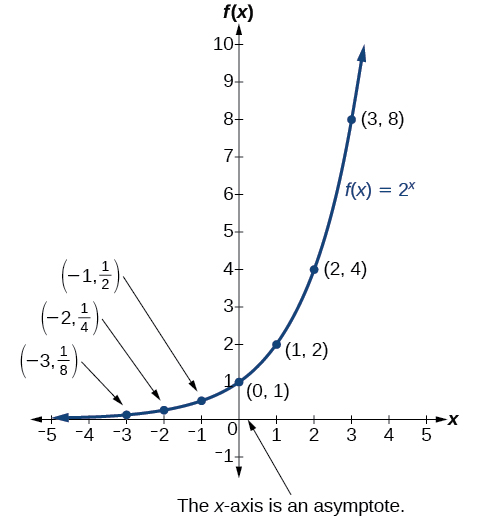
Figure 1. Notice that the graph gets close to the x-axis, but never touches it.
The domain of[latex]\,f\left(x\right)={2}^{x}\,[/latex]is all real numbers, the range is[latex]\,\left(0,\infty \right),[/latex] and the horizontal asymptote is[latex]\,y=0.[/latex]
To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form[latex]\,f\left(x\right)={b}^{x}\,[/latex]whose base is between zero and one. We’ll use the function[latex]\,g\left(x\right)={\left(\frac{1}{2}\right)}^{x}.\,[/latex]Observe how the output values in (Figure) change as the input increases by[latex]\,1.[/latex]
| [latex]x[/latex] | [latex]-3[/latex] | [latex]-2[/latex] | [latex]-1[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] |
| [latex]g(x)=\left(\frac{1}{2}\right)^{x}[/latex] | [latex]8[/latex] | [latex]4[/latex] | [latex]2[/latex] | [latex]1[/latex] | [latex]\frac{1}{2}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{8}[/latex] |
Again, because the input is increasing by 1, each output value is the product of the previous output and the base, or constant ratio[latex]\,\frac{1}{2}.[/latex]
Notice from the table that
- the output values are positive for all values of[latex]\,x;[/latex]
- as[latex]\,x\,[/latex]increases, the output values grow smaller, approaching zero; and
- as[latex]\,x\,[/latex]decreases, the output values grow without bound.
(Figure) shows the exponential decay function,[latex]\,g\left(x\right)={\left(\frac{1}{2}\right)}^{x}.[/latex]
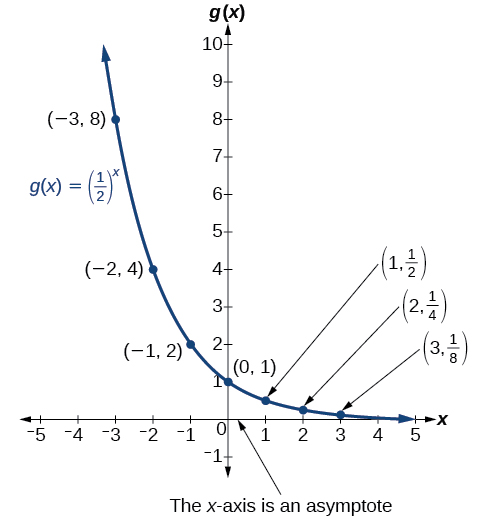
Figure 2.
The domain of[latex]\,g\left(x\right)={\left(\frac{1}{2}\right)}^{x}\,[/latex]is all real numbers, the range is[latex]\,\left(0,\infty \right),[/latex]and the horizontal asymptote is[latex]\,y=0.[/latex]
Characteristics of the Graph of the Parent Function f(x) = bx
An exponential function with the form[latex]\,f\left(x\right)={b}^{x},[/latex][latex]\,b>0,[/latex][latex]\,b\ne 1,[/latex]has these characteristics:
- one-to-one function
- horizontal asymptote:[latex]\,y=0[/latex]
- domain:[latex]\,\left(–\infty , \infty \right)[/latex]
- range:[latex]\,\left(0,\infty \right)[/latex]
- x-intercept: none
- y-intercept:[latex]\,\left(0,1\right)\,[/latex]
- increasing if[latex]\,b>1[/latex]
- decreasing if[latex]\,b<1[/latex]
(Figure) compares the graphs of exponential growth and decay functions.

Figure 3.
How To
Given an exponential function of the form[latex]\,f\left(x\right)={b}^{x},[/latex]graph the function.
- Create a table of points.
- Plot at least[latex]\,3\,[/latex]point from the table, including the y-intercept[latex]\,\left(0,1\right).[/latex]
- Draw a smooth curve through the points.
- State the domain,[latex]\,\left(-\infty ,\infty \right),[/latex]the range,[latex]\,\left(0,\infty \right),[/latex]and the horizontal asymptote, [latex]\,y=0.[/latex]
Sketching the Graph of an Exponential Function of the Form f(x) = bx
Sketch a graph of[latex]\,f\left(x\right)={0.25}^{x}.\,[/latex]State the domain, range, and asymptote.
Try It
Sketch the graph of[latex]\,f\left(x\right)={4}^{x}.\,[/latex]State the domain, range, and asymptote.
Graphing Transformations of Exponential Functions
Transformations of exponential graphs behave similarly to those of other functions. Just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function[latex]\,f\left(x\right)={b}^{x}\,[/latex]without loss of shape. For instance, just as the quadratic function maintains its parabolic shape when shifted, reflected, stretched, or compressed, the exponential function also maintains its general shape regardless of the transformations applied.
Graphing a Vertical Shift
The first transformation occurs when we add a constant[latex]\,d\,[/latex]to the parent function[latex]\,f\left(x\right)={b}^{x},[/latex] giving us a vertical shift[latex]\,d\,[/latex]units in the same direction as the sign. For example, if we begin by graphing a parent function,[latex]\,f\left(x\right)={2}^{x},[/latex] we can then graph two vertical shifts alongside it, using[latex]\,d=3:\,[/latex]the upward shift,[latex]\,g\left(x\right)={2}^{x}+3\,[/latex]and the downward shift,[latex]\,h\left(x\right)={2}^{x}-3.\,[/latex]Both vertical shifts are shown in (Figure).

Figure 5.
Observe the results of shifting[latex]\,f\left(x\right)={2}^{x}\,[/latex]vertically:
- The domain,[latex]\,\left(-\infty ,\infty \right)\,[/latex]remains unchanged.
- When the function is shifted up[latex]\,3\,[/latex]units to[latex]\,g\left(x\right)={2}^{x}+3:[/latex]
- The y-intercept shifts up[latex]\,3\,[/latex]units to[latex]\,\left(0,4\right).[/latex]
- The asymptote shifts up[latex]\,3\,[/latex]units to[latex]\,y=3.[/latex]
- The range becomes[latex]\,\left(3,\infty \right).[/latex]
- When the function is shifted down[latex]\,3\,[/latex]units to[latex]\,h\left(x\right)={2}^{x}-3:[/latex]
- The y-intercept shifts down[latex]\,3\,[/latex]units to[latex]\,\left(0,-2\right).[/latex]
- The asymptote also shifts down[latex]\,3\,[/latex]units to[latex]\,y=-3.[/latex]
- The range becomes[latex]\,\left(-3,\infty \right).[/latex]
Graphing a Horizontal Shift
The next transformation occurs when we add a constant[latex]\,c\,[/latex]to the input of the parent function[latex]\,f\left(x\right)={b}^{x},[/latex] giving us a horizontal shift[latex]\,c\,[/latex]units in the opposite direction of the sign. For example, if we begin by graphing the parent function[latex]\,f\left(x\right)={2}^{x},[/latex] we can then graph two horizontal shifts alongside it, using[latex]\,c=3:\,[/latex]the shift left,[latex]\,g\left(x\right)={2}^{x+3},[/latex] and the shift right,[latex]\,h\left(x\right)={2}^{x-3}.\,[/latex]Both horizontal shifts are shown in (Figure).

Figure 6.
Observe the results of shifting[latex]\,f\left(x\right)={2}^{x}\,[/latex]horizontally:
- The domain,[latex]\,\left(-\infty ,\infty \right),[/latex]remains unchanged.
- The asymptote,[latex]\,y=0,[/latex]remains unchanged.
- The y-intercept shifts such that:
- When the function is shifted left[latex]\,3\,[/latex]units to[latex]\,g\left(x\right)={2}^{x+3},[/latex]the y-intercept becomes[latex]\,\left(0,8\right).\,[/latex]This is because[latex]\,{2}^{x+3}=\left(8\right){2}^{x},[/latex]so the initial value of the function is[latex]\,8.[/latex]
- When the function is shifted right[latex]\,3\,[/latex]units to[latex]\,h\left(x\right)={2}^{x-3},[/latex]the y-intercept becomes[latex]\,\left(0,\frac{1}{8}\right).\,[/latex]Again, see that[latex]\,{2}^{x-3}=\left(\frac{1}{8}\right){2}^{x},[/latex]so the initial value of the function is[latex]\,\frac{1}{8}.[/latex]
Shifts of the Parent Function f(x) = bx
For any constants[latex]\,c\,[/latex]and[latex]\,d,[/latex]the function[latex]\,f\left(x\right)={b}^{x+c}+d\,[/latex]shifts the parent function[latex]\,f\left(x\right)={b}^{x}[/latex]
- vertically[latex]\,d\,[/latex]units, in the same direction of the sign of[latex]\,d.[/latex]
- horizontally[latex]\,c\,[/latex]units, in the opposite direction of the sign of[latex]\,c.[/latex]
- The y-intercept becomes[latex]\,\left(0,{b}^{c}+d\right).[/latex]
- The horizontal asymptote becomes[latex]\,y=d.[/latex]
- The range becomes[latex]\,\left(d,\infty \right).[/latex]
- The domain,[latex]\,\left(-\infty ,\infty \right),[/latex]remains unchanged.
How To
Given an exponential function with the form[latex]\,f\left(x\right)={b}^{x+c}+d,[/latex]graph the translation.
- Draw the horizontal asymptote[latex]\,y=d.[/latex]
- Identify the shift as[latex]\,\left(-c,d\right).\,[/latex]Shift the graph of[latex]\,f\left(x\right)={b}^{x}\,[/latex]left[latex]\,c\,[/latex]units if[latex]\,c\,[/latex]is positive, and right[latex]\,c\,[/latex]units if[latex]c\,[/latex]is negative.
- Shift the graph of[latex]\,f\left(x\right)={b}^{x}\,[/latex]up[latex]\,d\,[/latex]units if[latex]\,d\,[/latex]is positive, and down[latex]\,d\,[/latex]units if[latex]\,d\,[/latex]is negative.
- State the domain,[latex]\,\left(-\infty ,\infty \right),[/latex]the range,[latex]\,\left(d,\infty \right),[/latex]and the horizontal asymptote[latex]\,y=d.[/latex]
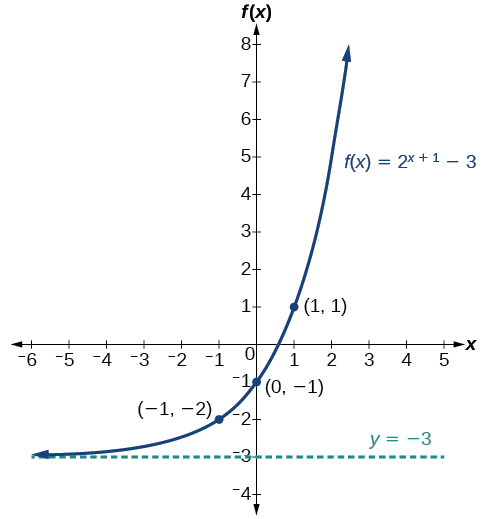
Graphing a Shift of an Exponential Function
Graph[latex]\,f\left(x\right)={2}^{x+1}-3.\,[/latex]State the domain, range, and asymptote.
Try It
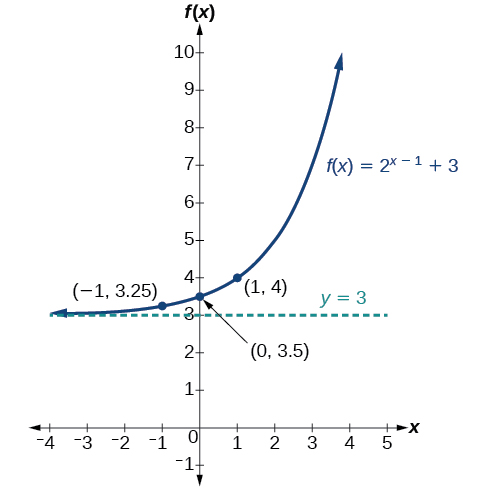
Graph[latex]\,f\left(x\right)={2}^{x-1}+3.\,[/latex]State domain, range, and asymptote.
How To
Given an equation of the form[latex]\,f\left(x\right)={b}^{x+c}+d\,[/latex]for[latex]\,x,[/latex] use a graphing calculator to approximate the solution.
- Press [Y=]. Enter the given exponential equation in the line headed “Y1=”.
- Enter the given value for[latex]\,f\left(x\right)\,[/latex]in the line headed “Y2=”.
- Press [WINDOW]. Adjust the y-axis so that it includes the value entered for “Y2=”.
- Press [GRAPH] to observe the graph of the exponential function along with the line for the specified value of[latex]\,f\left(x\right).[/latex]
- To find the value of[latex]\,x,[/latex]we compute the point of intersection. Press [2ND] then [CALC]. Select “intersect” and press [ENTER] three times. The point of intersection gives the value of x for the indicated value of the function.
Approximating the Solution of an Exponential Equation
Solve[latex]\,42=1.2{\left(5\right)}^{x}+2.8\,[/latex]graphically. Round to the nearest thousandth.
Try It
Solve[latex]\,4=7.85{\left(1.15\right)}^{x}-2.27\,[/latex]graphically. Round to the nearest thousandth.
Graphing a Stretch or Compression
While horizontal and vertical shifts involve adding constants to the input or to the function itself, a stretch or compression occurs when we multiply the parent function[latex]\,f\left(x\right)={b}^{x}\,[/latex]by a constant[latex]\,|a|>0.\,[/latex]For example, if we begin by graphing the parent function[latex]\,f\left(x\right)={2}^{x},[/latex]we can then graph the stretch, using[latex]\,a=3,[/latex]to get[latex]\,g\left(x\right)=3{\left(2\right)}^{x}\,[/latex]as shown on the left in (Figure), and the compression, using[latex]\,a=\frac{1}{3},[/latex]to get[latex]\,h\left(x\right)=\frac{1}{3}{\left(2\right)}^{x}\,[/latex]as shown on the right in (Figure).

Figure 8. (a)[latex]\,g\left(x\right)=3{\left(2\right)}^{x}\,[/latex]stretches the graph of[latex]\,f\left(x\right)={2}^{x}\,[/latex]vertically by a factor of[latex]\,3.\,[/latex](b)[latex]\,h\left(x\right)=\frac{1}{3}{\left(2\right)}^{x}\,[/latex]compresses the graph of[latex]\,f\left(x\right)={2}^{x}\,[/latex]vertically by a factor of[latex]\,\frac{1}{3}.[/latex]
Stretches and Compressions of the Parent Function f(x) = bx
For any factor[latex]\,a>0,[/latex]the function[latex]\,f\left(x\right)=a{\left(b\right)}^{x}[/latex]
- is stretched vertically by a factor of[latex]\,a\,[/latex]if[latex]\,|a|>1.[/latex]
- is compressed vertically by a factor of[latex]\,a\,[/latex]if[latex]\,|a|<1.[/latex]
- has a y-intercept of[latex]\,\left(0,a\right).[/latex]
- has a horizontal asymptote at[latex]\,y=0,[/latex] a range of[latex]\,\left(0,\infty \right),[/latex] and a domain of[latex]\,\left(-\infty ,\infty \right),[/latex]which are unchanged from the parent function.
Graphing the Stretch of an Exponential Function
Sketch a graph of[latex]\,f\left(x\right)=4{\left(\frac{1}{2}\right)}^{x}.\,[/latex]State the domain, range, and asymptote.
Try It
Sketch the graph of[latex]\,f\left(x\right)=\frac{1}{2}{\left(4\right)}^{x}.\,[/latex]State the domain, range, and asymptote.
Graphing Reflections
In addition to shifting, compressing, and stretching a graph, we can also reflect it about the x-axis or the y-axis. When we multiply the parent function[latex]\,f\left(x\right)={b}^{x}\,[/latex]by[latex]\,-1,[/latex]we get a reflection about the x-axis. When we multiply the input by[latex]\,-1,[/latex]we get a reflection about the y-axis. For example, if we begin by graphing the parent function[latex]\,f\left(x\right)={2}^{x},[/latex] we can then graph the two reflections alongside it. The reflection about the x-axis,[latex]\,g\left(x\right)={-2}^{x},[/latex]is shown on the left side of (Figure), and the reflection about the y-axis[latex]\,h\left(x\right)={2}^{-x},[/latex] is shown on the right side of (Figure).

Figure 10. (a)[latex]\,g\left(x\right)=-{2}^{x}\,[/latex]reflects the graph of[latex]\,f\left(x\right)={2}^{x}\,[/latex]about the x-axis. (b)[latex]\,g\left(x\right)={2}^{-x}\,[/latex]reflects the graph of[latex]\,f\left(x\right)={2}^{x}\,[/latex]about the y-axis.
Reflections of the Parent Function f(x) = bx
The function[latex]\,f\left(x\right)=-{b}^{x}[/latex]
- reflects the parent function[latex]\,f\left(x\right)={b}^{x}\,[/latex]about the x-axis.
- has a y-intercept of[latex]\,\left(0,-1\right).[/latex]
- has a range of[latex]\,\left(-\infty ,0\right)[/latex]
- has a horizontal asymptote at[latex]\,y=0\,[/latex]and domain of[latex]\,\left(-\infty ,\infty \right),[/latex]which are unchanged from the parent function.
The function[latex]\,f\left(x\right)={b}^{-x}[/latex]
- reflects the parent function[latex]\,f\left(x\right)={b}^{x}\,[/latex]about the y-axis.
- has a y-intercept of[latex]\,\left(0,1\right),[/latex] a horizontal asymptote at[latex]\,y=0,[/latex] a range of[latex]\,\left(0,\infty \right),[/latex] and a domain of[latex]\,\left(-\infty ,\infty \right),[/latex] which are unchanged from the parent function.
Writing and Graphing the Reflection of an Exponential Function
Find and graph the equation for a function,[latex]\,g\left(x\right),[/latex]that reflects[latex]\,f\left(x\right)={\left(\frac{1}{4}\right)}^{x}\,[/latex]about the x-axis. State its domain, range, and asymptote.
Try It
Find and graph the equation for a function,[latex]\,g\left(x\right),[/latex] that reflects[latex]\,f\left(x\right)={1.25}^{x}\,[/latex]about the y-axis. State its domain, range, and asymptote.
Summarizing Translations of the Exponential Function
Now that we have worked with each type of translation for the exponential function, we can summarize them in (Figure) to arrive at the general equation for translating exponential functions.
1, and notes the following changes: the reflected function is decreasing as x moves from 0 to infinity, the asymptote remains x=0, the x-intercept remains (1, 0), the key point changes to (b^(-1), 1), the domain remains (0, infinity), and the range remains (-infinity, infinity). The second column shows the left shift of the equation g(x)=log_b(x) when b>1, and notes the following changes: the reflected function is decreasing as x moves from 0 to infinity, the asymptote remains x=0, the x-intercept changes to (-1, 0), the key point changes to (-b, 1), the domain changes to (-infinity, 0), and the range remains (-infinity, infinity).”>
| Translations of the Parent Function [latex]\,f\left(x\right)={b}^{x}[/latex] | |
|---|---|
| Translation | Form |
Shift
|
[latex]f\left(x\right)={b}^{x+c}+d[/latex] |
Stretch and Compress
|
[latex]f\left(x\right)=a{b}^{x}[/latex] |
| Reflect about the x-axis | [latex]f\left(x\right)=-{b}^{x}[/latex] |
| Reflect about the y-axis | [latex]f\left(x\right)={b}^{-x}={\left(\frac{1}{b}\right)}^{x}[/latex] |
| General equation for all translations | [latex]f\left(x\right)=a{b}^{x+c}+d[/latex] |
Translations of Exponential Functions
A translation of an exponential function has the form
Where the parent function,[latex]\,y={b}^{x},[/latex][latex]\,b>1,[/latex]is
- shifted horizontally[latex]\,c\,[/latex]units to the left.
- stretched vertically by a factor of[latex]\,|a|\,[/latex]if[latex]\,|a|>0.[/latex]
- compressed vertically by a factor of[latex]\,|a|\,[/latex]if[latex]\,0<|a|<1.[/latex]
- shifted vertically[latex]\,d\,[/latex]units.
- reflected about the x-axis when[latex]\,a<0.[/latex]
Note the order of the shifts, transformations, and reflections follow the order of operations.
Writing a Function from a Description
Write the equation for the function described below. Give the horizontal asymptote, the domain, and the range.
- [latex]f\left(x\right)={e}^{x}\,[/latex]is vertically stretched by a factor of[latex]\,2\,[/latex], reflected across the y-axis, and then shifted up[latex]\,4\,[/latex]units.
Try It
Write the equation for function described below. Give the horizontal asymptote, the domain, and the range.
- [latex]f\left(x\right)={e}^{x}\,[/latex]is compressed vertically by a factor of[latex]\,\frac{1}{3},[/latex] reflected across the x-axis and then shifted down [latex]\,2[/latex] units.
Access this online resource for additional instruction and practice with graphing exponential functions.
Key Equations
| General Form for the Translation of the Parent Function[latex]\text{ }f\left(x\right)={b}^{x}[/latex] | [latex]f\left(x\right)=a{b}^{x+c}+d[/latex] |
Key Concepts
- The graph of the function[latex]\,f\left(x\right)={b}^{x}\,[/latex]has a y-intercept at[latex]\,\left(0, 1\right),[/latex]domain[latex]\,\left(-\infty , \infty \right),[/latex]range[latex]\,\left(0, \infty \right),[/latex] and horizontal asymptote[latex]\,y=0.\,[/latex]See (Figure).
- If[latex]\,b>1,[/latex]the function is increasing. The left tail of the graph will approach the asymptote[latex]\,y=0,[/latex] and the right tail will increase without bound.
- If[latex]\,0
- The equation[latex]\,f\left(x\right)={b}^{x}+d\,[/latex]represents a vertical shift of the parent function[latex]\,f\left(x\right)={b}^{x}.[/latex]
- The equation[latex]\,f\left(x\right)={b}^{x+c}\,[/latex]represents a horizontal shift of the parent function[latex]\,f\left(x\right)={b}^{x}.\,[/latex]See (Figure).
- Approximate solutions of the equation[latex]\,f\left(x\right)={b}^{x+c}+d\,[/latex]can be found using a graphing calculator. See (Figure).
- The equation[latex]\,f\left(x\right)=a{b}^{x},[/latex] where[latex]\,a>0,[/latex] represents a vertical stretch if[latex]\,|a|>1\,[/latex]or compression if[latex]\,0<|a|<1\,[/latex]of the parent function[latex]\,f\left(x\right)={b}^{x}.\,[/latex]See (Figure).
- When the parent function[latex]\,f\left(x\right)={b}^{x}\,[/latex]is multiplied by[latex]\,-1,[/latex]the result,[latex]\,f\left(x\right)=-{b}^{x},[/latex] is a reflection about the x-axis. When the input is multiplied by[latex]\,-1,[/latex]the result,[latex]\,f\left(x\right)={b}^{-x},[/latex] is a reflection about the y-axis. See (Figure).
- All translations of the exponential function can be summarized by the general equation[latex]\,f\left(x\right)=a{b}^{x+c}+d.\,[/latex]See (Figure).
- Using the general equation[latex]\,f\left(x\right)=a{b}^{x+c}+d,[/latex] we can write the equation of a function given its description. See (Figure).
Section Exercises
Verbal
What role does the horizontal asymptote of an exponential function play in telling us about the end behavior of the graph?
What is the advantage of knowing how to recognize transformations of the graph of a parent function algebraically?
Algebraic
The graph of[latex]\,f\left(x\right)={3}^{x}\,[/latex]is reflected about the y-axis and stretched vertically by a factor of[latex]\,4.\,[/latex]What is the equation of the new function,[latex]\,g\left(x\right)?\,[/latex]State its y-intercept, domain, and range.
The graph of[latex]\,f\left(x\right)={\left(\frac{1}{2}\right)}^{-x}\,[/latex]is reflected about the y-axis and compressed vertically by a factor of[latex]\,\frac{1}{5}.\,[/latex]What is the equation of the new function,[latex]\,g\left(x\right)?\,[/latex]State its y-intercept, domain, and range.
The graph of[latex]\,f\left(x\right)={10}^{x}\,[/latex]is reflected about the x-axis and shifted upward[latex]\,7\,[/latex]units. What is the equation of the new function,[latex]\,g\left(x\right)?\,[/latex]State its y-intercept, domain, and range.
The graph of[latex]\,f\left(x\right)={\left(1.68\right)}^{x}\,[/latex]is shifted right[latex]\,3\,[/latex]units, stretched vertically by a factor of[latex]\,2,[/latex]reflected about the x-axis, and then shifted downward[latex]\,3\,[/latex]units. What is the equation of the new function,[latex]\,g\left(x\right)?\,[/latex]State its y-intercept (to the nearest thousandth), domain, and range.
The graph of[latex]\,f\left(x\right)=2{\left(\frac{1}{4}\right)}^{x-20}[/latex] is shifted left[latex]\,2\,[/latex]units, stretched vertically by a factor of[latex]\,4,[/latex]reflected about the x-axis, and then shifted downward[latex]\,4\,[/latex]units. What is the equation of the new function,[latex]\,g\left(x\right)?\,[/latex]State its y-intercept, domain, and range.
Graphical
For the following exercises, graph the function and its reflection about the y-axis on the same axes, and give the y-intercept.
[latex]f\left(x\right)=3{\left(\frac{1}{2}\right)}^{x}[/latex]
[latex]g\left(x\right)=-2{\left(0.25\right)}^{x}[/latex]
[latex]h\left(x\right)=6{\left(1.75\right)}^{-x}[/latex]
For the following exercises, graph each set of functions on the same axes.
[latex]f\left(x\right)=3{\left(\frac{1}{4}\right)}^{x},[/latex][latex]g\left(x\right)=3{\left(2\right)}^{x},[/latex]and[latex]\,h\left(x\right)=3{\left(4\right)}^{x}[/latex]
[latex]f\left(x\right)=\frac{1}{4}{\left(3\right)}^{x},[/latex][latex]g\left(x\right)=2{\left(3\right)}^{x},[/latex]and[latex]\,h\left(x\right)=4{\left(3\right)}^{x}[/latex]
For the following exercises, match each function with one of the graphs in (Figure).

Figure 12.
[latex]f\left(x\right)=2{\left(0.69\right)}^{x}[/latex]
[latex]f\left(x\right)=2{\left(0.81\right)}^{x}[/latex]
[latex]f\left(x\right)=4{\left(1.28\right)}^{x}[/latex]
[latex]f\left(x\right)=2{\left(1.59\right)}^{x}[/latex]
[latex]f\left(x\right)=4{\left(0.69\right)}^{x}[/latex]
For the following exercises, use the graphs shown in (Figure). All have the form[latex]\,f\left(x\right)=a{b}^{x}.[/latex]

Figure 13.
Which graph has the largest value for[latex]\,b?[/latex]
Which graph has the smallest value for[latex]\,b?[/latex]
Which graph has the largest value for[latex]\,a?[/latex]
Which graph has the smallest value for[latex]\,a?[/latex]
For the following exercises, graph the function and its reflection about the x-axis on the same axes.
[latex]f\left(x\right)=\frac{1}{2}{\left(4\right)}^{x}[/latex]
[latex]f\left(x\right)=3{\left(0.75\right)}^{x}-1[/latex]
[latex]f\left(x\right)=-4{\left(2\right)}^{x}+2[/latex]
For the following exercises, graph the transformation of[latex]\,f\left(x\right)={2}^{x}.\,[/latex]Give the horizontal asymptote, the domain, and the range.
[latex]f\left(x\right)={2}^{-x}[/latex]
[latex]h\left(x\right)={2}^{x}+3[/latex]
[latex]f\left(x\right)={2}^{x-2}[/latex]
For the following exercises, describe the end behavior of the graphs of the functions.
[latex]f\left(x\right)=-5{\left(4\right)}^{x}-1[/latex]
[latex]f\left(x\right)=3{\left(\frac{1}{2}\right)}^{x}-2[/latex]
[latex]f\left(x\right)=3{\left(4\right)}^{-x}+2[/latex]
For the following exercises, start with the graph of[latex]\,f\left(x\right)={4}^{x}.\,[/latex]Then write a function that results from the given transformation.
Shift [latex]f\left(x\right)[/latex] 4 units upward
Shift[latex]\,f\left(x\right)\,[/latex]3 units downward
Shift[latex]\,f\left(x\right)\,[/latex]2 units left
Shift[latex]\,f\left(x\right)\,[/latex]5 units right
Reflect[latex]\,f\left(x\right)\,[/latex]about the x-axis
Reflect[latex]\,f\left(x\right)\,[/latex]about the y-axis
For the following exercises, each graph is a transformation of[latex]\,y={2}^{x}.\,[/latex]Write an equation describing the transformation.



For the following exercises, find an exponential equation for the graph.


Numeric
For the following exercises, evaluate the exponential functions for the indicated value of[latex]\,x.[/latex]
[latex]g\left(x\right)=\frac{1}{3}{\left(7\right)}^{x-2}\,[/latex]for[latex]\,g\left(6\right).[/latex]
[latex]f\left(x\right)=4{\left(2\right)}^{x-1}-2\,[/latex]for[latex]\,f\left(5\right).[/latex]
[latex]h\left(x\right)=-\frac{1}{2}{\left(\frac{1}{2}\right)}^{x}+6\,[/latex]for[latex]\,h\left(-7\right).[/latex]
Technology
For the following exercises, use a graphing calculator to approximate the solutions of the equation. Round to the nearest thousandth.
[latex]-50=-{\left(\frac{1}{2}\right)}^{-x}[/latex]
[latex]12=2{\left(3\right)}^{x}+1[/latex]
[latex]5=3{\left(\frac{1}{2}\right)}^{x-1}-2[/latex]
[latex]-30=-4{\left(2\right)}^{x+2}+2[/latex]
Extensions
Explore and discuss the graphs of[latex]\,F\left(x\right)={\left(b\right)}^{x}\,[/latex]and[latex]\,G\left(x\right)={\left(\frac{1}{b}\right)}^{x}.\,[/latex]Then make a conjecture about the relationship between the graphs of the functions[latex]\,{b}^{x}\,[/latex]and[latex]\,{\left(\frac{1}{b}\right)}^{x}\,[/latex]for any real number[latex]\,b>0.[/latex]
Prove the conjecture made in the previous exercise.
Explore and discuss the graphs of[latex]\,f\left(x\right)={4}^{x},[/latex][latex]\,g\left(x\right)={4}^{x-2},[/latex]and[latex]\,h\left(x\right)=\left(\frac{1}{16}\right){4}^{x}.\,[/latex]Then make a conjecture about the relationship between the graphs of the functions[latex]\,{b}^{x}\,[/latex]and[latex]\,\left(\frac{1}{{b}^{n}}\right){b}^{x}\,[/latex]for any real number n and real number[latex]\,b>0.[/latex]
Prove the conjecture made in the previous exercise.
Candela Citations
- Algebra and Trigonometry. Authored by: Jay Abramson, et. al. Provided by: OpenStax CNX. Located at: http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1