Rotation of Axes

arning Objectives

In this section, you will:

Identify nondegenerate conic sections given their general form equations.
Use rotation of axes formulas.
Write equations of rotated conics in standard form.
Identify conics without rotating axes.

Figure 1. The nondegenerate conic sections

As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions, which we also call a cone. The way in which we slice the cone will determine the type of conic section formed at the intersection. A circle is formed by slicing a cone with a plane perpendicular to the axis of symmetry of the cone. An ellipse is formed by slicing a single cone with a slanted plane not perpendicular to the axis of symmetry. A parabola is formed by slicing the plane through the top or bottom of the double-cone, whereas a hyperbola is formed when the plane slices both the top and bottom of the cone. See (Figure).

Figure 2. Degenerate conic sections

Ellipses, circles, hyperbolas, and parabolas are sometimes called the nondegenerate conic sections, in contrast to the degenerate conic sections, which are shown in (Figure). A degenerate conic results when a plane intersects the double cone and passes through the apex. Depending on the angle of the plane, three types of degenerate conic sections are possible: a point, a line, or two intersecting lines.

Identifying Nondegenerate Conics in General Form

In previous sections of this chapter, we have focused on the standard form equations for nondegenerate conic sections. In this section, we will shift our focus to the general form equation, which can be used for any conic. The general form is set equal to zero, and the terms and coefficients are given in a particular order, as shown below.

[latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0[/latex]

where[latex]\,A,B,[/latex] and [latex]\,C\,[/latex]are not all zero. We can use the values of the coefficients to identify which type conic is represented by a given equation.

You may notice that the general form equation has an[latex]\,xy\,[/latex]term that we have not seen in any of the standard form equations. As we will discuss later, the[latex]\,xy\,[/latex]term rotates the conic whenever[latex]\text{ }B\text{ }[/latex]is not equal to zero.

Conic Sections	Example
ellipse	[latex]4{x}^{2}+9{y}^{2}=1[/latex]
circle	[latex]4{x}^{2}+4{y}^{2}=1[/latex]
hyperbola	[latex]4{x}^{2}-9{y}^{2}=1[/latex]
parabola	[latex]4{x}^{2}=9y\text{ or }4{y}^{2}=9x[/latex]
one line	[latex]4x+9y=1[/latex]
intersecting lines	[latex]\left(x-4\right)\left(y+4\right)=0[/latex]
parallel lines	[latex]\left(x-4\right)\left(x-9\right)=0[/latex]
a point	[latex]4{x}^{2}+4{y}^{2}=0[/latex]
no graph	[latex]4{x}^{2}+4{y}^{2}=\,-\,1[/latex]

General Form of Conic Sections

A conic section has the general form

[latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0[/latex]

where[latex]\,A,B,[/latex] and[latex]\,C\,[/latex]are not all zero.

(Figure) summarizes the different conic sections where[latex]\,B=0,[/latex] and[latex]\,A\,[/latex]and[latex]\,C\,[/latex]are nonzero real numbers. This indicates that the conic has not been rotated.

ellipse	[latex]A{x}^{2}+C{y}^{2}+Dx+Ey+F=0,\text{ }A\ne C\text{ and }AC>0[/latex]
circle	[latex]A{x}^{2}+C{y}^{2}+Dx+Ey+F=0,\text{ }A=C[/latex]
hyperbola	[latex]A{x}^{2}-C{y}^{2}+Dx+Ey+F=0\text{ or }-A{x}^{2}+C{y}^{2}+Dx+Ey+F=0,[/latex]where[latex]\,A\,[/latex]and[latex]\,C\,[/latex]are positive
parabola	[latex]A{x}^{2}+Dx+Ey+F=0\text{ or }C{y}^{2}+Dx+Ey+F=0[/latex]

How To

Given the equation of a conic, identify the type of conic.

Rewrite the equation in the general form, [latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0.[/latex]
Identify the values of[latex]\,A\,[/latex]and[latex]\,C\,[/latex]from the general form.
1. If[latex]\,A\,[/latex]and[latex]\,C\,[/latex] are nonzero, have the same sign, and are not equal to each other, then the graph may be an ellipse.
2. If[latex]\,A\,[/latex]and[latex]\,C\,[/latex]are equal and nonzero and have the same sign, then the graph may be a circle.
3. If[latex]\,A\,[/latex]and[latex]\,C\,[/latex]are nonzero and have opposite signs, then the graph may be a hyperbola.
4. If either[latex]\,A\,[/latex]or[latex]\,C\,[/latex] is zero, then the graph may be a parabola.
If B = 0, the conic section will have a vertical and/or horizontal axes. If B does not equal 0, as shown below, the conic section is rotated. Notice the phrase “may be” in the definitions. That is because the equation may not represent a conic section at all, depending on the values of A, B, C, D, E, and F. For example, the degenerate case of a circle or an ellipse is a point:

[latex]A{x}^{2}+B{y}^{2}=0\text{,}[/latex]when A and B have the same sign.

The degenerate case of a hyperbola is two intersecting straight lines:[latex]A{x}^{2}+B{y}^{2}=0\text{,}[/latex]when A and B have opposite signs.

On the other hand, the equation, [latex]A{x}^{2}+B{y}^{2}+1=0\text{,}[/latex] when A and B are positive does not represent a graph at all, since there are no real ordered pairs which satisfy it.

Identifying a Conic from Its General Form

Identify the graph of each of the following nondegenerate conic sections.

[latex]4{x}^{2}-9{y}^{2}+36x+36y-125=0[/latex]
[latex]9{y}^{2}+16x+36y-10=0[/latex]
[latex]3{x}^{2}+3{y}^{2}-2x-6y-4=0[/latex]
[latex]-25{x}^{2}-4{y}^{2}+100x+16y+20=0[/latex]

Show Solution

Try It

Identify the graph of each of the following nondegenerate conic sections.

[latex]16{y}^{2}-{x}^{2}+x-4y-9=0[/latex]
[latex]16{x}^{2}+4{y}^{2}+16x+49y-81=0[/latex]

Show Solution

Finding a New Representation of the Given Equation after Rotating through a Given Angle

Until now, we have looked at equations of conic sections without an[latex]\,xy\,[/latex]term, which aligns the graphs with the x– and y-axes. When we add an[latex]\,xy\,[/latex]term, we are rotating the conic about the origin. If the x– and y-axes are rotated through an angle, say[latex]\,\theta ,[/latex]then every point on the plane may be thought of as having two representations:[latex]\,\left(x,y\right)\,[/latex]on the Cartesian plane with the original x-axis and y-axis, and[latex]\,\left({x}^{\prime },{y}^{\prime }\right)\,[/latex]on the new plane defined by the new, rotated axes, called the x’-axis and y’-axis. See (Figure).

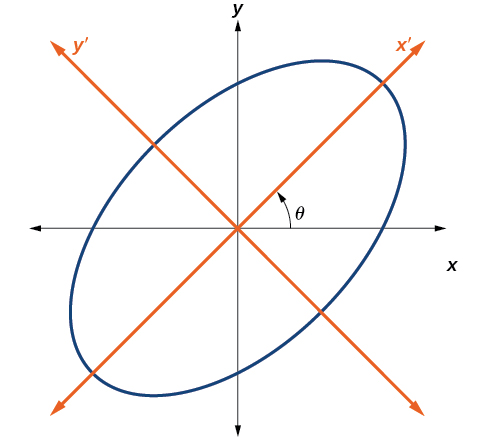
Figure 3. The graph of the rotated ellipse[latex]\,{x}^{2}+{y}^{2}–xy–15=0[/latex]

We will find the relationships between[latex]\,x\,[/latex]and[latex]\,y\,[/latex]on the Cartesian plane with[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime }\,[/latex]on the new rotated plane. See (Figure).

Figure 4. The Cartesian plane with x- and y-axes and the resulting x′− and y′−axes formed by a rotation by an angle[latex]\text{ }\theta .[/latex]

The original coordinate x– and y-axes have unit vectors[latex]\,i\,[/latex]and[latex]\,j\,.[/latex]The rotated coordinate axes have unit vectors[latex]\,{i}^{\prime }\,[/latex]and[latex]\,{j}^{\prime }.[/latex]The angle[latex]\,\theta \,[/latex]is known as the angle of rotation. See (Figure). We may write the new unit vectors in terms of the original ones.

[latex]\begin{array}{l}{i}^{\prime }=\mathrm{cos}\text{ }\theta i+\mathrm{sin}\text{ }\theta j\hfill \\ {j}^{\prime }=-\mathrm{sin}\text{ }\theta i+\mathrm{cos}\text{ }\theta j\hfill \end{array}[/latex]

Figure 5. Relationship between the old and new coordinate planes.

Consider a vector[latex]\,u\,[/latex]in the new coordinate plane. It may be represented in terms of its coordinate axes.

[latex]\begin{array}{ll}u={x}^{\prime }{i}^{\prime }+{y}^{\prime }{j}^{\prime }\hfill & \hfill \\ u={x}^{\prime }\left(i\text{ }\mathrm{cos}\text{ }\theta +j\text{ }\mathrm{sin}\text{ }\theta \right)+{y}^{\prime }\left(-i\text{ }\mathrm{sin}\text{ }\theta +j\text{ }\mathrm{cos}\text{ }\theta \right)\hfill & \begin{array}{cccc}& & & \end{array}\text{Substitute}.\hfill \\ u=ix\text{'}\text{ }\mathrm{cos}\text{ }\theta +jx\text{'}\text{ }\mathrm{sin}\text{ }\theta -iy\text{'}\text{ }\mathrm{sin}\text{ }\theta +jy\text{'}\text{ }\mathrm{cos}\text{ }\theta \hfill & \begin{array}{cccc}& & & \end{array}\text{Distribute}.\hfill \\ u=ix\text{'}\text{ }\mathrm{cos}\text{ }\theta -iy\text{'}\text{ }\mathrm{sin}\text{ }\theta +jx\text{'}\text{ }\mathrm{sin}\text{ }\theta +jy\text{'}\text{ }\mathrm{cos}\text{ }\theta \hfill & \begin{array}{cccc}& & & \end{array}\text{Apply commutative property}.\hfill \\ u=\left(x\text{'}\text{ }\mathrm{cos}\text{ }\theta -y\text{'}\text{ }\mathrm{sin}\text{ }\theta \right)i+\left(x\text{'}\text{ }\mathrm{sin}\text{ }\theta +y\text{'}\text{ }\mathrm{cos}\text{ }\theta \right)j\hfill & \begin{array}{cccc}& & & \end{array}\text{Factor by grouping}.\hfill \end{array}[/latex]

Because[latex]\,u={x}^{\prime }{i}^{\prime }+{y}^{\prime }{j}^{\prime },[/latex] we have representations of[latex]\,x\,[/latex]and[latex]\,y\,[/latex]in terms of the new coordinate system.

[latex]\begin{array}{c}x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta \\ \text{and}\\ y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta \end{array}[/latex]

Equations of Rotation

If a point[latex]\,\left(x,y\right)\,[/latex]on the Cartesian plane is represented on a new coordinate plane where the axes of rotation are formed by rotating an angle[latex]\,\theta \,[/latex]from the positive x-axis, then the coordinates of the point with respect to the new axes are[latex]\,\left({x}^{\prime },{y}^{\prime }\right).\,[/latex]We can use the following equations of rotation to define the relationship between[latex]\,\left(x,y\right)\,[/latex]and[latex]\,\left({x}^{\prime },{y}^{\prime }\right):[/latex]

[latex]x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta[/latex]

and

[latex]y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta[/latex]

How To

Given the equation of a conic, find a new representation after rotating through an angle.

Find[latex]\,x\,[/latex]and[latex]\,y\,[/latex]where[latex]\,x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta \,[/latex]and[latex]\,y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta .[/latex]
Substitute the expression for[latex]\,x\,[/latex]and[latex]\,y\,[/latex]into in the given equation, then simplify.
Write the equations with[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime }\,[/latex]in standard form.

Finding a New Representation of an Equation after Rotating through a Given Angle

Find a new representation of the equation[latex]\,2{x}^{2}-xy+2{y}^{2}-30=0\,[/latex]after rotating through an angle of[latex]\,\theta =45°.[/latex]

Show Solution

Find[latex]\,x\,[/latex]and[latex]\,y,[/latex]where[latex]\,x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta \,[/latex]and[latex]\,y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta .[/latex]

Because[latex]\,\theta =45°,[/latex]

[latex]\begin{array}{l}\hfill \\ x={x}^{\prime }\mathrm{cos}\left(45°\right)-{y}^{\prime }\mathrm{sin}\left(45°\right)\hfill \\ x={x}^{\prime }\left(\frac{1}{\sqrt{2}}\right)-{y}^{\prime }\left(\frac{1}{\sqrt{2}}\right)\hfill \\ x=\frac{{x}^{\prime }-{y}^{\prime }}{\sqrt{2}}\hfill \end{array}[/latex]

and

[latex]\begin{array}{l}\\ \begin{array}{l}y={x}^{\prime }\mathrm{sin}\left(45°\right)+{y}^{\prime }\mathrm{cos}\left(45°\right)\hfill \\ y={x}^{\prime }\left(\frac{1}{\sqrt{2}}\right)+{y}^{\prime }\left(\frac{1}{\sqrt{2}}\right)\hfill \\ y=\frac{{x}^{\prime }+{y}^{\prime }}{\sqrt{2}}\hfill \end{array}\end{array}[/latex]

Substitute[latex]\,x={x}^{\prime }\mathrm{cos}\theta -{y}^{\prime }\mathrm{sin}\theta \,[/latex]and[latex]\,y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta \,[/latex]into[latex]\,2{x}^{2}-xy+2{y}^{2}-30=0.[/latex]

[latex]2{\left(\frac{{x}^{\prime }-{y}^{\prime }}{\sqrt{2}}\right)}^{2}-\left(\frac{{x}^{\prime }-{y}^{\prime }}{\sqrt{2}}\right)\left(\frac{{x}^{\prime }+{y}^{\prime }}{\sqrt{2}}\right)+2{\left(\frac{{x}^{\prime }+{y}^{\prime }}{\sqrt{2}}\right)}^{2}-30=0[/latex]

Simplify.

[latex]\begin{array}{ll}\overline{)2}\frac{\left({x}^{\prime }-{y}^{\prime }\right)\left({x}^{\prime }-{y}^{\prime }\right)}{\overline{)2}}-\frac{\left({x}^{\prime }-{y}^{\prime }\right)\left({x}^{\prime }+{y}^{\prime }\right)}{2}+\overline{)2}\frac{\left({x}^{\prime }+{y}^{\prime }\right)\left({x}^{\prime }+{y}^{\prime }\right)}{\overline{)2}}-30=0\hfill & \begin{array}{cccc}& & & \end{array}\text{FOIL method}\hfill \\ \text{ }{x}^{\prime }{}^{2}{\overline{)-2{x}^{\prime }y}}^{\prime }+{y}^{\prime }{}^{2}-\frac{\left({x}^{\prime }{}^{2}-{y}^{\prime }{}^{2}\right)}{2}+{x}^{\prime }{}^{2}\overline{)+2{x}^{\prime }{y}^{\prime }}+{y}^{\prime }{}^{2}-30=0\hfill & \begin{array}{cccc}& & & \end{array}\text{Combine like terms}.\hfill \\ \text{ }2{x}^{\prime }{}^{2}+2{y}^{\prime }{}^{2}-\frac{\left({x}^{\prime }{}^{2}-{y}^{\prime }{}^{2}\right)}{2}=30\hfill & \begin{array}{cccc}& & & \end{array}\text{Combine like terms}.\hfill \\ \text{ }2\left(2{x}^{\prime }{}^{2}+2{y}^{\prime }{}^{2}-\frac{\left({x}^{\prime }{}^{2}-{y}^{\prime }{}^{2}\right)}{2}\right)=2\left(30\right)\hfill & \begin{array}{cccc}& & & \end{array}\text{Multiply both sides by 2}.\hfill \\ \text{ }4{x}^{\prime }{}^{2}+4{y}^{\prime }{}^{2}-\left({x}^{\prime }{}^{2}-{y}^{\prime }{}^{2}\right)=60\hfill & \begin{array}{cccc}& & & \end{array}\text{Simplify}.\hfill \\ \text{ }4{x}^{\prime }{}^{2}+4{y}^{\prime }{}^{2}-{x}^{\prime }{}^{2}+{y}^{\prime }{}^{2}=60\hfill & \begin{array}{cccc}& & & \end{array}\text{Distribute}.\hfill \\ \text{ }\frac{3{x}^{\prime }{}^{2}}{60}+\frac{5{y}^{\prime }{}^{2}}{60}=\frac{60}{60}\hfill & \begin{array}{cccc}& & & \end{array}\text{Set equal to 1}.\hfill \end{array}[/latex]

Write the equations with[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime }\,[/latex]in the standard form.

[latex]\frac{{{x}^{\prime }}^{2}}{20}+\frac{{{y}^{\prime }}^{2}}{12}=1[/latex]

This equation is an ellipse. (Figure) shows the graph.

Figure 6.

Writing Equations of Rotated Conics in Standard Form

Now that we can find the standard form of a conic when we are given an angle of rotation, we will learn how to transform the equation of a conic given in the form[latex]\,A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0\,[/latex]into standard form by rotating the axes. To do so, we will rewrite the general form as an equation in the[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime }\,[/latex]coordinate system without the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]term, by rotating the axes by a measure of[latex]\,\theta \,[/latex]that satisfies

[latex]\mathrm{cot}\left(2\theta \right)=\frac{A-C}{B}[/latex]

We have learned already that any conic may be represented by the second degree equation

[latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0[/latex]

where[latex]\,A,B,[/latex]and[latex]\,C\,[/latex]are not all zero. However, if[latex]\,B\ne 0,[/latex] then we have an[latex]\,xy\,[/latex]term that prevents us from rewriting the equation in standard form. To eliminate it, we can rotate the axes by an acute angle[latex]\,\theta \,[/latex]where[latex]\,\mathrm{cot}\left(2\theta \right)=\frac{A-C}{B}.[/latex]

If[latex]\,\mathrm{cot}\left(2\theta \right)>0,[/latex] then[latex]\,2\theta \,[/latex] is in the first quadrant, and[latex]\,\theta \,[/latex] is between[latex]\,\left(0°,45°\right).[/latex]
If[latex]\,\mathrm{cot}\left(2\theta \right)<0,[/latex] then[latex]\,2\theta \,[/latex] is in the second quadrant, and[latex]\,\theta \,[/latex] is between[latex]\,\left(45°,90°\right).[/latex]
If[latex]\,A=C,[/latex] then[latex]\,\theta =45°.[/latex]

How To

Given an equation for a conic in the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]system, rewrite the equation without the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]term in terms of[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime },[/latex]where the[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime }\,[/latex]axes are rotations of the standard axes by[latex]\,\theta \,[/latex]degrees.

Find[latex]\,\mathrm{cot}\left(2\theta \right).[/latex]
Find[latex]\,\mathrm{sin}\text{ }\theta \,[/latex]and[latex]\,\mathrm{cos}\text{ }\theta .[/latex]
Substitute[latex]\,\mathrm{sin}\text{ }\theta \,[/latex]and[latex]\,\mathrm{cos}\text{ }\theta \,[/latex]into[latex]\,x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta \,[/latex]and[latex]\,y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta .[/latex]
Substitute the expression for[latex]\,x\,[/latex]and[latex]\,y\,[/latex]into in the given equation, and then simplify.
Write the equations with[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime }\,[/latex]in the standard form with respect to the rotated axes.

Rewriting an Equation with respect to the x′ and y′ axes without the x′y′ Term

Rewrite the equation[latex]\,8{x}^{2}-12xy+17{y}^{2}=20\,[/latex]in the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]system without an[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]term.

Show Solution

First, we find[latex]\,\mathrm{cot}\left(2\theta \right).\,[/latex]See (Figure).

[latex]\begin{array}{l}8{x}^{2}-12xy+17{y}^{2}=20⇒A=8,\,B=-12\,\text{and}\,C=17\hfill \\ \text{ }\,\,\,\mathrm{cot}\left(2\theta \right)=\frac{A-C}{B}=\frac{8-17}{-12}\hfill \\ \text{ }\,\,\,\mathrm{cot}\left(2\theta \right)=\frac{-9}{-12}=\frac{3}{4}\hfill \end{array}[/latex]

Figure 7.

[latex]\mathrm{cot}\left(2\theta \right)=\frac{3}{4}=\frac{\text{adjacent}}{\text{opposite}}[/latex]

So the hypotenuse is

[latex]\begin{array}{r}\hfill {3}^{2}+{4}^{2}={h}^{2}\\ \hfill 9+16={h}^{2}\\ \hfill 25={h}^{2}\\ \hfill h=5\,\,\,\end{array}[/latex]

Next, we find[latex]\,\mathrm{sin}\text{ }\theta[/latex] and [latex]\mathrm{cos}\text{ }\theta .[/latex]

[latex]\begin{array}{l}\begin{array}{l}\hfill \\ \hfill \\ \mathrm{sin}\text{ }\theta =\sqrt{\frac{1-\mathrm{cos}\left(2\theta \right)}{2}}=\sqrt{\frac{1-\frac{3}{5}}{2}}=\sqrt{\frac{\frac{5}{5}-\frac{3}{5}}{2}}=\sqrt{\frac{5-3}{5}\cdot \frac{1}{2}}=\sqrt{\frac{2}{10}}=\sqrt{\frac{1}{5}}\hfill \end{array}\hfill \\ \mathrm{sin}\text{ }\theta =\frac{1}{\sqrt{5}}\hfill \\ \mathrm{cos}\text{ }\theta =\sqrt{\frac{1+\mathrm{cos}\left(2\theta \right)}{2}}=\sqrt{\frac{1+\frac{3}{5}}{2}}=\sqrt{\frac{\frac{5}{5}+\frac{3}{5}}{2}}=\sqrt{\frac{5+3}{5}\cdot \frac{1}{2}}=\sqrt{\frac{8}{10}}=\sqrt{\frac{4}{5}}\hfill \\ \mathrm{cos}\text{ }\theta =\frac{2}{\sqrt{5}}\hfill \end{array}[/latex]

Substitute the values of[latex]\,\mathrm{sin}\text{ }\theta \,[/latex]and[latex]\,\mathrm{cos}\text{ }\theta \,[/latex]into[latex]\,x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta \,[/latex]and[latex]\,y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta .[/latex]

[latex]\begin{array}{l}\hfill \\ \begin{array}{l}x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta \hfill \\ x={x}^{\prime }\left(\frac{2}{\sqrt{5}}\right)-{y}^{\prime }\left(\frac{1}{\sqrt{5}}\right)\hfill \\ x=\frac{2{x}^{\prime }-{y}^{\prime }}{\sqrt{5}}\hfill \end{array}\hfill \end{array}[/latex]

and

[latex]\begin{array}{l}\begin{array}{l}\hfill \\ y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta \hfill \end{array}\hfill \\ y={x}^{\prime }\left(\frac{1}{\sqrt{5}}\right)+{y}^{\prime }\left(\frac{2}{\sqrt{5}}\right)\hfill \\ y=\frac{{x}^{\prime }+2{y}^{\prime }}{\sqrt{5}}\hfill \end{array}[/latex]

Substitute the expressions for[latex]\,x\,[/latex]and[latex]\,y\,[/latex]into in the given equation, and then simplify.

[latex]\begin{array}{l}\text{ }8{\left(\frac{2{x}^{\prime }-{y}^{\prime }}{\sqrt{5}}\right)}^{2}-12\left(\frac{2{x}^{\prime }-{y}^{\prime }}{\sqrt{5}}\right)\left(\frac{{x}^{\prime }+2{y}^{\prime }}{\sqrt{5}}\right)+17{\left(\frac{{x}^{\prime }+2{y}^{\prime }}{\sqrt{5}}\right)}^{2}=20\text{ }\hfill \\ \text{ }8\left(\frac{\left(2{x}^{\prime }-{y}^{\prime }\right)\left(2{x}^{\prime }-{y}^{\prime }\right)}{5}\right)-12\left(\frac{\left(2{x}^{\prime }-{y}^{\prime }\right)\left({x}^{\prime }+2{y}^{\prime }\right)}{5}\right)+17\left(\frac{\left({x}^{\prime }+2{y}^{\prime }\right)\left({x}^{\prime }+2{y}^{\prime }\right)}{5}\right)=20\text{ }\hfill \\ \text{ }8\left(4{x}^{\prime }{}^{2}-4{x}^{\prime }{y}^{\prime }+{y}^{\prime }{}^{2}\right)-12\left(2{x}^{\prime }{}^{2}+3{x}^{\prime }{y}^{\prime }-2{y}^{\prime }{}^{2}\right)+17\left({x}^{\prime }{}^{2}+4{x}^{\prime }{y}^{\prime }+4{y}^{\prime }{}^{2}\right)=100\hfill \\ 32{x}^{\prime }{}^{2}-32{x}^{\prime }{y}^{\prime }+8{y}^{\prime }{}^{2}-24{x}^{\prime }{}^{2}-36{x}^{\prime }{y}^{\prime }+24{y}^{\prime }{}^{2}+17{x}^{\prime }{}^{2}+68{x}^{\prime }{y}^{\prime }+68{y}^{\prime }{}^{2}=100\hfill \\ \text{ }25{x}^{\prime }{}^{2}+100{y}^{\prime }{}^{2}=100\text{ }\hfill \\ \text{ }\frac{25}{100}{x}^{\prime }{}^{2}+\frac{100}{100}{y}^{\prime }{}^{2}=\frac{100}{100} \hfill \end{array}[/latex]

Write the equations with[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime }\,[/latex]in the standard form with respect to the new coordinate system.

[latex]\frac{{{x}^{\prime }}^{2}}{4}+\frac{{{y}^{\prime }}^{2}}{1}=1[/latex]

(Figure) shows the graph of the ellipse.

Figure 8.

Try It

Rewrite the[latex]\,13{x}^{2}-6\sqrt{3}xy+7{y}^{2}=16\,[/latex]in the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]system without the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]term.

Show Solution

Graphing an Equation That Has No x′y′ Terms

Graph the following equation relative to the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]system:

[latex]{x}^{2}+12xy-4{y}^{2}=30[/latex]

Show Solution

First, we find[latex]\,\mathrm{cot}\left(2\theta \right).[/latex]

[latex]{x}^{2}+12xy-4{y}^{2}=20⇒A=1,\text{ }B=12,\text{and }C=-4[/latex]

[latex]\begin{array}{l}\mathrm{cot}\left(2\theta \right)=\frac{A-C}{B}\hfill \\ \mathrm{cot}\left(2\theta \right)=\frac{1-\left(-4\right)}{12}\hfill \\ \mathrm{cot}\left(2\theta \right)=\frac{5}{12}\hfill \end{array}[/latex]

Because[latex]\,\mathrm{cot}\left(2\theta \right)=\frac{5}{12},[/latex] we can draw a reference triangle as in (Figure).

Figure 9.

[latex]\mathrm{cot}\left(2\theta \right)=\frac{5}{12}=\frac{\text{adjacent}}{\text{opposite}}[/latex]

Thus, the hypotenuse is

[latex]\begin{array}{r}\hfill {5}^{2}+{12}^{2}={h}^{2}\\ \hfill 25+144={h}^{2}\\ \hfill 169={h}^{2}\\ \hfill h=13\end{array}[/latex]

Next, we find[latex]\,\mathrm{sin}\text{ }\theta \,[/latex]and[latex]\,\mathrm{cos}\text{ }\theta .\,[/latex]We will use half-angle identities.

[latex]\begin{array}{l}\begin{array}{l}\hfill \\ \hfill \\ \mathrm{sin}\text{ }\theta =\sqrt{\frac{1-\mathrm{cos}\left(2\theta \right)}{2}}=\sqrt{\frac{1-\frac{5}{13}}{2}}=\sqrt{\frac{\frac{13}{13}-\frac{5}{13}}{2}}=\sqrt{\frac{8}{13}\cdot \frac{1}{2}}=\frac{2}{\sqrt{13}}\hfill \end{array}\hfill \\ \mathrm{cos}\text{ }\theta =\sqrt{\frac{1+\mathrm{cos}\left(2\theta \right)}{2}}=\sqrt{\frac{1+\frac{5}{13}}{2}}=\sqrt{\frac{\frac{13}{13}+\frac{5}{13}}{2}}=\sqrt{\frac{18}{13}\cdot \frac{1}{2}}=\frac{3}{\sqrt{13}}\hfill \end{array}[/latex]

Now we find[latex]\,x\,[/latex]and[latex]\,y\text{.\hspace{0.17em}}[/latex]

[latex]\begin{array}{l}\hfill \\ x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta \hfill \\ x={x}^{\prime }\left(\frac{3}{\sqrt{13}}\right)-{y}^{\prime }\left(\frac{2}{\sqrt{13}}\right)\hfill \\ x=\frac{3{x}^{\prime }-2{y}^{\prime }}{\sqrt{13}}\hfill \end{array}[/latex]

and

[latex]\begin{array}{l}\hfill \\ y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta \hfill \\ y={x}^{\prime }\left(\frac{2}{\sqrt{13}}\right)+{y}^{\prime }\left(\frac{3}{\sqrt{13}}\right)\hfill \\ y=\frac{2{x}^{\prime }+3{y}^{\prime }}{\sqrt{13}}\hfill \end{array}[/latex]

Now we substitute[latex]\,x=\frac{3{x}^{\prime }-2{y}^{\prime }}{\sqrt{13}}\,[/latex]and[latex]\,y=\frac{2{x}^{\prime }+3{y}^{\prime }}{\sqrt{13}}\,[/latex]into[latex]\,{x}^{2}+12xy-4{y}^{2}=30.[/latex]

[latex]\begin{array}{llll}\text{ }{\left(\frac{3{x}^{\prime }-2{y}^{\prime }}{\sqrt{13}}\right)}^{2}+12\left(\frac{3{x}^{\prime }-2{y}^{\prime }}{\sqrt{13}}\right)\left(\frac{2{x}^{\prime }+3{y}^{\prime }}{\sqrt{13}}\right)-4{\left(\frac{2{x}^{\prime }+3{y}^{\prime }}{\sqrt{13}}\right)}^{2}=30\hfill & \hfill & \hfill & \hfill \\ \text{ }\,\,\left(\frac{1}{13}\right)\left[{\left(3{x}^{\prime }-2{y}^{\prime }\right)}^{2}+12\left(3{x}^{\prime }-2{y}^{\prime }\right)\left(2{x}^{\prime }+3{y}^{\prime }\right)-4{\left(2{x}^{\prime }+3{y}^{\prime }\right)}^{2}\right]=30 \hfill & \hfill & \hfill & \text{Factor}.\hfill \\ \left(\frac{1}{13}\right)\left[9{x}^{\prime }{}^{2}-12{x}^{\prime }{y}^{\prime }+4{y}^{\prime }{}^{2}+12\left(6{x}^{\prime }{}^{2}+5{x}^{\prime }{y}^{\prime }-6{y}^{\prime }{}^{2}\right)-4\left(4{x}^{\prime }{}^{2}+12{x}^{\prime }{y}^{\prime }+9{y}^{\prime }{}^{2}\right)\right]=30\hfill & \hfill & \hfill & \text{Multiply}.\hfill \\ \text{ }\left(\frac{1}{13}\right)\left[9{x}^{\prime }{}^{2}-12{x}^{\prime }{y}^{\prime }+4{y}^{\prime }{}^{2}+72{x}^{\prime }{}^{2}+60{x}^{\prime }{y}^{\prime }-72{y}^{\prime }{}^{2}-16{x}^{\prime }{}^{2}-48{x}^{\prime }{y}^{\prime }-36{y}^{\prime }{}^{2}\right]=30\hfill & \hfill & \hfill & \text{Distribute}.\hfill \\ \text{ }\,\text{ }\left(\frac{1}{13}\right)\left[65{x}^{\prime }{}^{2}-104{y}^{\prime }{}^{2}\right]=30\hfill & \hfill & \hfill & \text{Combine like terms}.\hfill \\ \text{ }65{x}^{\prime }{}^{2}-104{y}^{\prime }{}^{2}=390\hfill & \hfill & \hfill & \text{Multiply}.\text{ }\hfill \\ \text{ }\frac{{x}^{\prime }{}^{2}}{6}-\frac{4{y}^{\prime }{}^{2}}{15}=1 \hfill & \hfill & \hfill & \text{Divide by 390}.\hfill \end{array}[/latex]

(Figure) shows the graph of the hyperbola[latex]\,\frac{{{x}^{\prime }}^{2}}{6}-\frac{4{{y}^{\prime }}^{2}}{15}=1.\text{ }[/latex]

Figure 10.

Identifying Conics without Rotating Axes

Now we have come full circle. How do we identify the type of conic described by an equation? What happens when the axes are rotated? Recall, the general form of a conic is

[latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0[/latex]

If we apply the rotation formulas to this equation we get the form

[latex]{A}^{\prime }{{x}^{\prime }}^{2}+{B}^{\prime }{x}^{\prime }{y}^{\prime }+{C}^{\prime }{{y}^{\prime }}^{2}+{D}^{\prime }{x}^{\prime }+{E}^{\prime }{y}^{\prime }+{F}^{\prime }=0[/latex]

It may be shown that[latex]\,{B}^{2}-4AC={{B}^{\prime }}^{2}-4{A}^{\prime }{C}^{\prime }.\,[/latex]The expression does not vary after rotation, so we call the expression invariant. The discriminant,[latex]\,{B}^{2}-4AC,[/latex] is invariant and remains unchanged after rotation. Because the discriminant remains unchanged, observing the discriminant enables us to identify the conic section.

Using the Discriminant to Identify a Conic

If the equation[latex]\,A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0\,[/latex]is transformed by rotating axes into the equation[latex]\,{A}^{\prime }{{x}^{\prime }}^{2}+{B}^{\prime }{x}^{\prime }{y}^{\prime }+{C}^{\prime }{{y}^{\prime }}^{2}+{D}^{\prime }{x}^{\prime }+{E}^{\prime }{y}^{\prime }+{F}^{\prime }=0,[/latex] then[latex]\,{B}^{2}-4AC={{B}^{\prime }}^{2}-4{A}^{\prime }{C}^{\prime }.[/latex]

The equation[latex]\,A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0\,[/latex]is an ellipse, a parabola, or a hyperbola, or a degenerate case of one of these.

If the discriminant,[latex]\,{B}^{2}-4AC,[/latex]is

[latex]<0,[/latex] the conic section is an ellipse
[latex]=0,[/latex] the conic section is a parabola
[latex]>0,[/latex] the conic section is a hyperbola

Identifying the Conic without Rotating Axes

Identify the conic for each of the following without rotating axes.

[latex]5{x}^{2}+2\sqrt{3}xy+2{y}^{2}-5=0[/latex]
[latex]5{x}^{2}+2\sqrt{3}xy+12{y}^{2}-5=0[/latex]

Show Solution

Try It

Identify the conic for each of the following without rotating axes.

[latex]{x}^{2}-9xy+3{y}^{2}-12=0[/latex]
[latex]10{x}^{2}-9xy+4{y}^{2}-4=0[/latex]

Show Solution

Access this online resource for additional instruction and practice with conic sections and rotation of axes.

Introduction to Conic Sections

Key Equations

General Form equation of a conic section	[latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0[/latex]
Rotation of a conic section	[latex]\begin{array}{l}x={x}^{\prime }\mathrm{cos}\text{ }\theta -{y}^{\prime }\mathrm{sin}\text{ }\theta \hfill \\ y={x}^{\prime }\mathrm{sin}\text{ }\theta +{y}^{\prime }\mathrm{cos}\text{ }\theta \hfill \end{array}[/latex]
Angle of rotation	[latex]\theta ,\text{where }\mathrm{cot}\left(2\theta \right)=\frac{A-C}{B}[/latex]

Key Concepts

Four basic shapes can result from the intersection of a plane with a pair of right circular cones connected tail to tail. They include an ellipse, a circle, a hyperbola, and a parabola.
A nondegenerate conic section has the general form[latex]\,A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0\,[/latex]where[latex]\,A,B\,[/latex]and[latex]\,C\,[/latex]are not all zero. The values of[latex]\,A,B,[/latex] and[latex]\,C\,[/latex]determine the type of conic. See (Figure).
Equations of conic sections with an[latex]\,xy\,[/latex]term have been rotated about the origin. See (Figure).
The general form can be transformed into an equation in the[latex]\,{x}^{\prime }\,[/latex]and[latex]\,{y}^{\prime }\,[/latex]coordinate system without the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]term. See (Figure) and (Figure).
An expression is described as invariant if it remains unchanged after rotating. Because the discriminant is invariant, observing it enables us to identify the conic section. See (Figure).

Section Exercises

Verbal

What effect does the[latex]\,xy\,[/latex]term have on the graph of a conic section?

Show Solution

If the equation of a conic section is written in the form[latex]\,A{x}^{2}+B{y}^{2}+Cx+Dy+E=0\,[/latex]and[latex]\,AB=0,[/latex] what can we conclude?

If the equation of a conic section is written in the form[latex]\,A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0,[/latex]and[latex]\,{B}^{2}-4AC>0,[/latex] what can we conclude?

Show Solution

Given the equation[latex]\,a{x}^{2}+4x+3{y}^{2}-12=0,[/latex] what can we conclude if[latex]\,a>0?[/latex]

For the equation[latex]\,A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0,[/latex] the value of[latex]\,\theta \,[/latex]that satisfies[latex]\,\mathrm{cot}\left(2\theta \right)=\frac{A-C}{B}\,[/latex]gives us what information?

Show Solution

Algebraic

For the following exercises, determine which conic section is represented based on the given equation.

[latex]9{x}^{2}+4{y}^{2}+72x+36y-500=0[/latex]

[latex]{x}^{2}-10x+4y-10=0[/latex]

Show Solution

[latex]2{x}^{2}-2{y}^{2}+4x-6y-2=0[/latex]

[latex]4{x}^{2}-{y}^{2}+8x-1=0[/latex]

Show Solution

[latex]4{y}^{2}-5x+9y+1=0[/latex]

[latex]2{x}^{2}+3{y}^{2}-8x-12y+2=0[/latex]

Show Solution

[latex]4{x}^{2}+9xy+4{y}^{2}-36y-125=0[/latex]

[latex]3{x}^{2}+6xy+3{y}^{2}-36y-125=0[/latex]

Show Solution

[latex]-3{x}^{2}+3\sqrt{3}xy-4{y}^{2}+9=0[/latex]

[latex]2{x}^{2}+4\sqrt{3}xy+6{y}^{2}-6x-3=0[/latex]

Show Solution

[latex]-{x}^{2}+4\sqrt{2}xy+2{y}^{2}-2y+1=0[/latex]

[latex]8{x}^{2}+4\sqrt{2}xy+4{y}^{2}-10x+1=0[/latex]

Show Solution

For the following exercises, find a new representation of the given equation after rotating through the given angle.

[latex]3{x}^{2}+xy+3{y}^{2}-5=0,\theta =45°[/latex]

[latex]4{x}^{2}-xy+4{y}^{2}-2=0,\theta =45°[/latex]

Show Solution

[latex]2{x}^{2}+8xy-1=0,\theta =30°[/latex]

[latex]-2{x}^{2}+8xy+1=0,\theta =45°[/latex]

Show Solution

[latex]4{x}^{2}+\sqrt{2}xy+4{y}^{2}+y+2=0,\theta =45°[/latex]

For the following exercises, determine the angle[latex]\,\theta \,[/latex]that will eliminate the[latex]\,xy\,[/latex]term and write the corresponding equation without the[latex]\,xy\,[/latex]term.

[latex]{x}^{2}+3\sqrt{3}xy+4{y}^{2}+y-2=0[/latex]

Show Solution

[latex]4{x}^{2}+2\sqrt{3}xy+6{y}^{2}+y-2=0[/latex]

[latex]9{x}^{2}-3\sqrt{3}xy+6{y}^{2}+4y-3=0[/latex]

Show Solution

[latex]-3{x}^{2}-\sqrt{3}xy-2{y}^{2}-x=0[/latex]

[latex]16{x}^{2}+24xy+9{y}^{2}+6x-6y+2=0[/latex]

Show Solution

[latex]{x}^{2}+4xy+4{y}^{2}+3x-2=0[/latex]

[latex]{x}^{2}+4xy+{y}^{2}-2x+1=0[/latex]

Show Solution

[latex]4{x}^{2}-2\sqrt{3}xy+6{y}^{2}-1=0[/latex]

Graphical

For the following exercises, rotate through the given angle based on the given equation. Give the new equation and graph the original and rotated equation.

[latex]y=-{x}^{2},\theta =-{45}^{\circ }[/latex]

Show Solution

[latex]x={y}^{2},\theta ={45}^{\circ }[/latex]

[latex]\frac{{x}^{2}}{4}+\frac{{y}^{2}}{1}=1,\theta ={45}^{\circ }[/latex]

Show Solution

[latex]\frac{{y}^{2}}{16}+\frac{{x}^{2}}{9}=1,\theta ={45}^{\circ }[/latex]

[latex]{y}^{2}-{x}^{2}=1,\theta ={45}^{\circ }[/latex]

Show Solution

[latex]y=\frac{{x}^{2}}{2},\theta ={30}^{\circ }[/latex]

[latex]x={\left(y-1\right)}^{2},\theta ={30}^{\circ }[/latex]

Show Solution

[latex]\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1,\theta ={30}^{\circ }[/latex]

For the following exercises, graph the equation relative to the[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]system in which the equation has no[latex]\,{x}^{\prime }{y}^{\prime }\,[/latex]term.

[latex]xy=9[/latex]

Show Solution

[latex]{x}^{2}+10xy+{y}^{2}-6=0[/latex]

[latex]{x}^{2}-10xy+{y}^{2}-24=0[/latex]

Show Solution

[latex]4{x}^{2}-3\sqrt{3}xy+{y}^{2}-22=0[/latex]

[latex]6{x}^{2}+2\sqrt{3}xy+4{y}^{2}-21=0[/latex]

Show Solution

[latex]11{x}^{2}+10\sqrt{3}xy+{y}^{2}-64=0[/latex]

[latex]21{x}^{2}+2\sqrt{3}xy+19{y}^{2}-18=0[/latex]

Show Solution

[latex]16{x}^{2}+24xy+9{y}^{2}-130x+90y=0[/latex]

[latex]16{x}^{2}+24xy+9{y}^{2}-60x+80y=0[/latex]

Show Solution

[latex]13{x}^{2}-6\sqrt{3}xy+7{y}^{2}-16=0[/latex]

[latex]4{x}^{2}-4xy+{y}^{2}-8\sqrt{5}x-16\sqrt{5}y=0[/latex]

Show Solution

For the following exercises, determine the angle of rotation in order to eliminate the[latex]\,xy\,[/latex]term. Then graph the new set of axes.

[latex]6{x}^{2}-5\sqrt{3}xy+{y}^{2}+10x-12y=0[/latex]

[latex]6{x}^{2}-5xy+6{y}^{2}+20x-y=0[/latex]

Show Solution

[latex]6{x}^{2}-8\sqrt{3}xy+14{y}^{2}+10x-3y=0[/latex]

[latex]4{x}^{2}+6\sqrt{3}xy+10{y}^{2}+20x-40y=0[/latex]

Show Solution

[latex]8{x}^{2}+3xy+4{y}^{2}+2x-4=0[/latex]

[latex]16{x}^{2}+24xy+9{y}^{2}+20x-44y=0[/latex]

Show Solution

For the following exercises, determine the value of[latex]\,k\,[/latex]based on the given equation.

Given[latex]\,4{x}^{2}+kxy+16{y}^{2}+8x+24y-48=0,[/latex] find[latex]\,k\,[/latex]for the graph to be a parabola.

Given[latex]\,2{x}^{2}+kxy+12{y}^{2}+10x-16y+28=0,[/latex] find[latex]\,k\,[/latex]for the graph to be an ellipse.

Show Solution

Given[latex]\,3{x}^{2}+kxy+4{y}^{2}-6x+20y+128=0,[/latex] find[latex]\,k\,[/latex]for the graph to be a hyperbola.

Given[latex]\,k{x}^{2}+8xy+8{y}^{2}-12x+16y+18=0,[/latex] find[latex]\,k\,[/latex]for the graph to be a parabola.

Show Solution

Given[latex]\,6{x}^{2}+12xy+k{y}^{2}+16x+10y+4=0,[/latex] find[latex]\,k\,[/latex]for the graph to be an ellipse.

Glossary

angle of rotation: an acute angle formed by a set of axes rotated from the Cartesian plane where, if[latex]\,\mathrm{cot}\left(2\theta \right)>0,[/latex]then[latex]\,\theta \,[/latex]is between[latex]\,\left(0°,45°\right);[/latex]if[latex]\,\mathrm{cot}\left(2\theta \right)<0,[/latex]then[latex]\,\theta \,[/latex]is between[latex]\,\left(45°,90°\right);\,[/latex]and if[latex]\,\mathrm{cot}\left(2\theta \right)=0,[/latex]then[latex]\,\theta =45°[/latex]

degenerate conic sections: any of the possible shapes formed when a plane intersects a double cone through the apex. Types of degenerate conic sections include a point, a line, and intersecting lines.

nondegenerate conic section: a shape formed by the intersection of a plane with a double right cone such that the plane does not pass through the apex; nondegenerate conics include circles, ellipses, hyperbolas, and parabolas

Analytic Geometry

arning Objectives

Identifying Nondegenerate Conics in General Form

General Form of Conic Sections

How To

Identifying a Conic from Its General Form

Try It

Finding a New Representation of the Given Equation after Rotating through a Given Angle

Equations of Rotation

How To

Finding a New Representation of an Equation after Rotating through a Given Angle

Writing Equations of Rotated Conics in Standard Form

How To

Rewriting an Equation with respect to the x′ and y′ axes without the x′y′ Term

Try It

Graphing an Equation That Has No x′y′ Terms

Identifying Conics without Rotating Axes

Using the Discriminant to Identify a Conic

Identifying the Conic without Rotating Axes

Try It

Key Equations

Key Concepts

Section Exercises

Verbal

Algebraic

Graphical

Glossary

Candela Citations